时间序列预测方法概述
机器学习与优化算法 2024-09-02 16:01:02 阅读 96
这里写目录标题
时间序列预测方法概述1.统计方法1.1 ARIMA (AutoRegressive Integrated Moving Average)1.2 State Space Models1.3 Exponential Smoothing
2.机器学习方法2.1 SVM (Support Vector Machines)2.2 RF (Random Forest)2.3 KNN (K-Nearest Neighbors)
3. 深度学习方法3.1 RNN (Recurrent Neural Networks)3.2 LSTM (Long Short-Term Memory)3.3 GRU (Gated Recurrent Units)3.4 1D-CNN (Convolutional Neural Networks)3.5 Temporal Convolutional Network (TCN)3.5 Transformer
参考文献
时间序列预测方法概述
时间序列预测是数据分析的一个重要领域,涉及对未来事件的预测,基于过去的数据点。以下是几种常用的时间序列预测方法,包括其原理、优缺点。
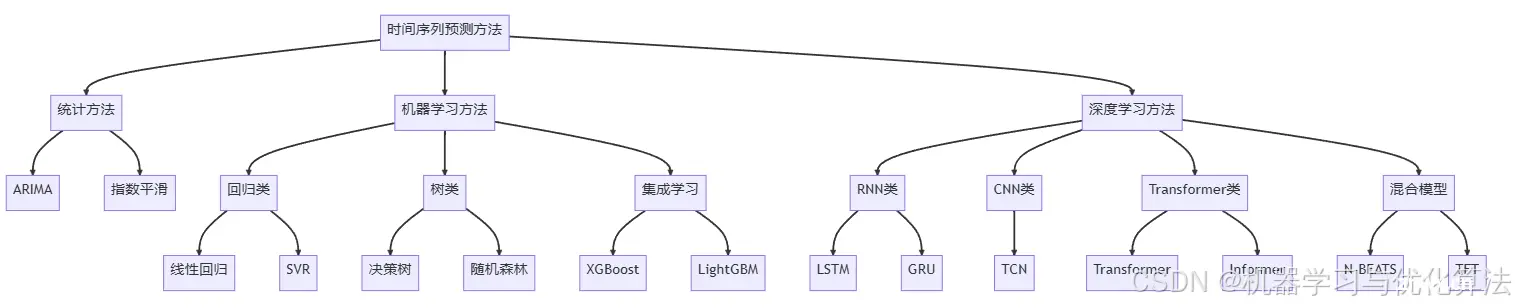
1.统计方法
1.1 ARIMA (AutoRegressive Integrated Moving Average)
原理:
ARIMA模型是一种用于非平稳时间序列分析和预测的方法。它结合了自回归(AR)、差分(I)和移动平均(MA)三个组件。
优点:
能够处理非平稳数据。在许多经济和商业应用中表现出色。
缺点:
需要对数据进行预处理,如差分,以达到平稳性。参数选择可能复杂且耗时。
<code>import pandas as pd
from statsmodels.tsa.arima.model import ARIMA
# 加载数据
data = pd.read_csv('your_data.csv')
data['Date'] = pd.to_datetime(data['Date'])
data.set_index('Date', inplace=True)
# 创建模型
model = ARIMA(data['Value'], order=(5,1,0))
model_fit = model.fit()
# 预测
forecast = model_fit.forecast(steps=10)
print(forecast)
1.2 State Space Models
原理:
状态空间模型是一类广泛使用的模型,特别适用于系统具有隐藏状态的情况,其中观测到的数据是这些隐藏状态的函数。
优点:
允许处理更复杂的动态关系。包括Kalman滤波器在内的方法可以实时更新预测。
缺点:
计算成本较高,尤其是在大数据集上。需要更多的先验知识来定义模型结构。
from statsmodels.tsa.statespace.sarimax import SARIMAX
# 使用SARIMAX实现State Space Models
model = SARIMAX(data['Value'], order=(1, 1, 1), seasonal_order=(1, 1, 1, 12))
results = model.fit()
# 预测
forecast = results.get_forecast(steps=10)
print(forecast.predicted_mean)
1.3 Exponential Smoothing
原理:
指数平滑法是一种预测技术,它使用加权平均数,其中较新的观测值被赋予更高的权重。
优点:
简单易用。适用于趋势和季节性数据。
缺点:
过于简单,在面对复杂模式时可能不够准确。
from statsmodels.tsa.holtwinters import ExponentialSmoothing
# 创建模型
model = ExponentialSmoothing(data['Value']).fit()
# 预测
forecast = model.forecast(10)
print(forecast)
2.机器学习方法
2.1 SVM (Support Vector Machines)
原理:
支持向量机可以应用于时间序列预测,通过找到最佳的超平面来区分数据点。
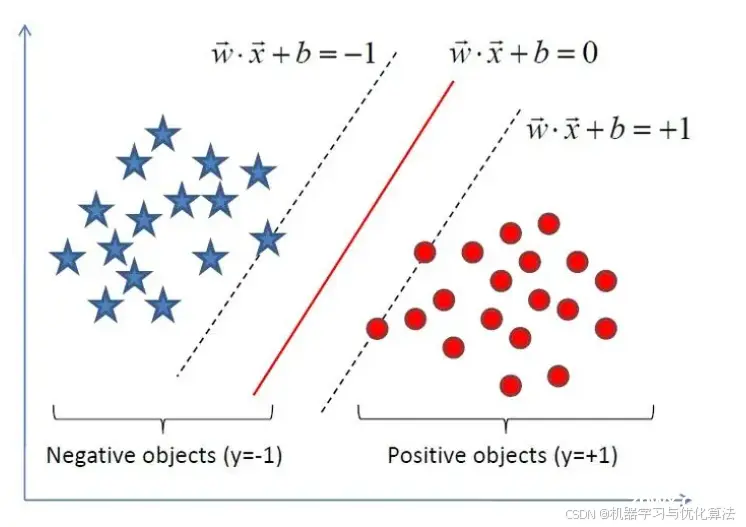
优点:
对噪声和异常值有较好的鲁棒性。在小样本数据集中表现良好。
缺点:
需要大量计算资源。对于大规模数据集效率较低。
<code>from sklearn.svm import SVR
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import make_pipeline
# 假设 'data' 是一个DataFrame,其中 'Value' 列是我们要预测的目标
X = data.index.values.reshape(-1, 1)
y = data['Value']
# 创建模型
model = make_pipeline(StandardScaler(), SVR())
# 训练模型
model.fit(X, y)
# 预测
forecast = model.predict(X[-10:])
print(forecast)
2.2 RF (Random Forest)
原理:
随机森林是一种集成学习方法,由多个决策树组成,每个树对数据的不同子集进行训练。
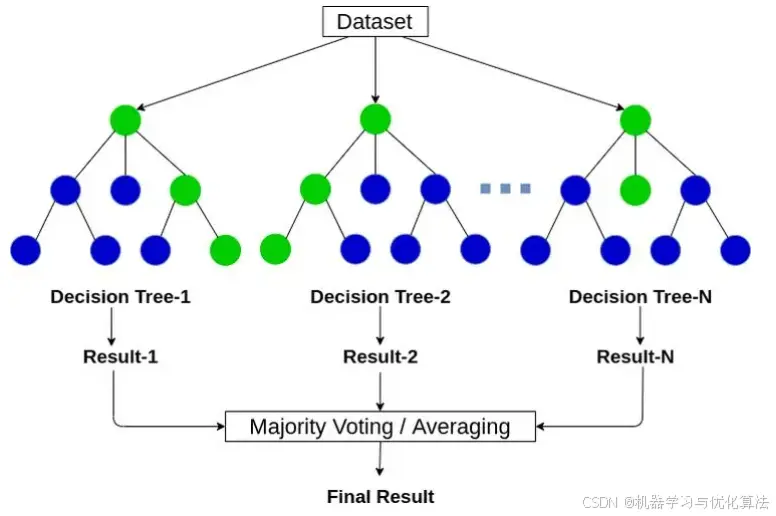
优点:
能够处理高维数据。减少了过拟合的风险。
缺点:
训练时间可能较长。解释性较差,难以直观理解预测过程。
<code>from sklearn.ensemble import RandomForestRegressor
# 创建模型
model = RandomForestRegressor(n_estimators=100)
# 训练模型
model.fit(X, y)
# 预测
forecast = model.predict(X[-10:])
print(forecast)
2.3 KNN (K-Nearest Neighbors)
原理:
K近邻算法通过寻找最相似的历史数据点来预测未来值。
优点:
实现简单,易于理解。不需要训练阶段。
缺点:
预测速度慢,尤其是在大数据库中。需要大量的存储空间。
from sklearn.neighbors import KNeighborsRegressor
# 创建模型
model = KNeighborsRegressor(n_neighbors=5)
# 训练模型
model.fit(X, y)
# 预测
forecast = model.predict(X[-10:])
print(forecast)
3. 深度学习方法
3.1 RNN (Recurrent Neural Networks)
详细介绍可以参考我的另一篇博客:RNN循环递归网络讲解与不掉包python实现
原理:
循环神经网络能够处理序列数据,通过反馈连接来保留历史信息。
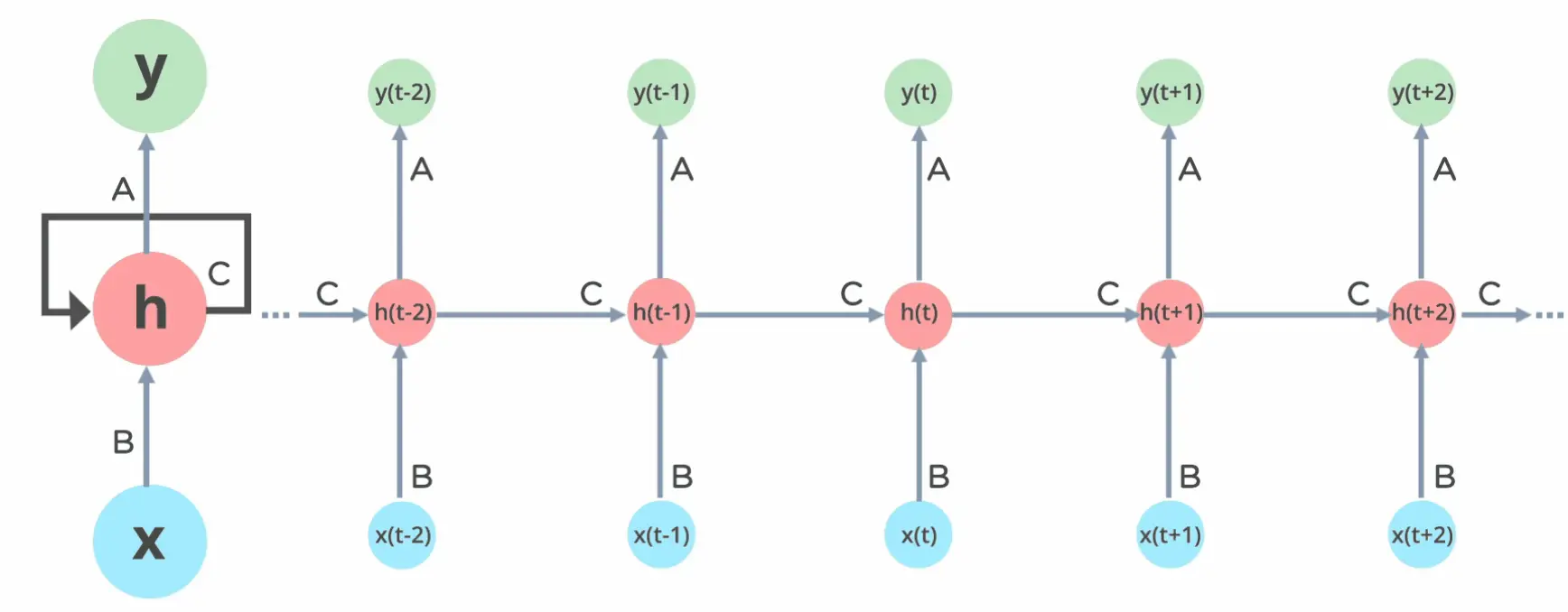
优点:
能够捕捉长期依赖关系。在语音识别和自然语言处理中非常有效。
缺点:
训练过程可能不稳定。长序列预测时容易发生梯度消失/爆炸问题。
<code>class RNN:
def __init__(self, input_size, hidden_size, output_size):
self.input_size = input_size
self.hidden_size = hidden_size
self.output_size = output_size
# 初始化权重
self.Wxh = np.random.randn(hidden_size, input_size) * 0.01
self.Whh = np.random.randn(hidden_size, hidden_size) * 0.01
self.Why = np.random.randn(output_size, hidden_size) * 0.01
# 初始化偏置
self.bh = np.zeros((hidden_size, 1))
self.by = np.zeros((output_size, 1))
# 初始化Adam优化器
self.optimizer = Adam({
'Wxh': self.Wxh, 'Whh': self.Whh, 'Why': self.Why,
'bh': self.bh, 'by': self.by
})
def forward(self, inputs):
h = np.zeros((self.hidden_size, 1))
self.last_inputs = inputs
self.last_hs = { 0: h}
# 前向传播
for t, x in enumerate(inputs):
h = np.tanh(np.dot(self.Wxh, x) + np.dot(self.Whh, h) + self.bh)
self.last_hs[t + 1] = h
y = np.dot(self.Why, h) + self.by
return y, h
def backward(self, d_y):
n = len(self.last_inputs)
# 初始化梯度
d_Wxh = np.zeros_like(self.Wxh)
d_Whh = np.zeros_like(self.Whh)
d_Why = np.zeros_like(self.Why)
d_bh = np.zeros_like(self.bh)
d_by = np.zeros_like(self.by)
d_h = np.dot(self.Why.T, d_y)
# 反向传播
for t in reversed(range(n)):
temp = (1 - self.last_hs[t + 1] ** 2) * d_h
d_Wxh += np.dot(temp, self.last_inputs[t].T)
d_Whh += np.dot(temp, self.last_hs[t].T)
d_bh += temp
d_h = np.dot(self.Whh.T, temp)
d_Why = np.dot(d_y, self.last_hs[n].T)
d_by = d_y
# 使用Adam优化器更新参数
self.optimizer.step({
'Wxh': d_Wxh, 'Whh': d_Whh, 'Why': d_Why,
'bh': d_bh, 'by': d_by
})
3.2 LSTM (Long Short-Term Memory)
原理:
长短期记忆网络是RNN的一种特殊类型,具有门控机制,可以更好地管理长期依赖。
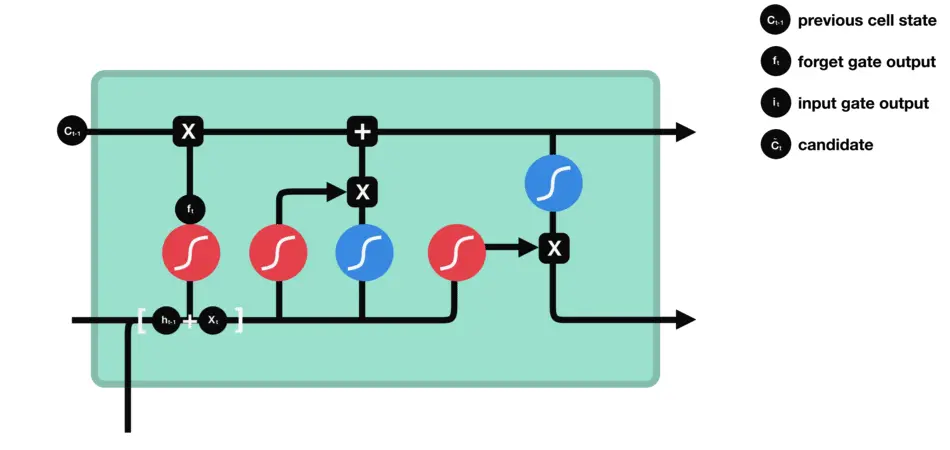
优点:
更好地解决了梯度消失/爆炸问题。在序列预测任务中性能优秀。
缺点:
结构复杂,训练成本高。需要较大的数据集进行训练。
<code>from keras.models import Sequential
from keras.layers import LSTM, Dense
# 数据预处理
X_train = data['Value'].values[:-1].reshape(-1, 1, 1)
y_train = data['Value'].values[1:].reshape(-1, 1)
# 创建模型
model = Sequential()
model.add(LSTM(50, activation='relu', input_shape=(1, 1)))code>
model.add(Dense(1))
model.compile(optimizer='adam', loss='mse')code>
# 训练模型
model.fit(X_train, y_train, epochs=100, verbose=0)
# 预测
X_test = data['Value'].values[-10:].reshape(-1, 1, 1)
forecast = model.predict(X_test)
print(forecast)
3.3 GRU (Gated Recurrent Units)
原理:
门控循环单元是LSTM的简化版本,减少了门的数量。
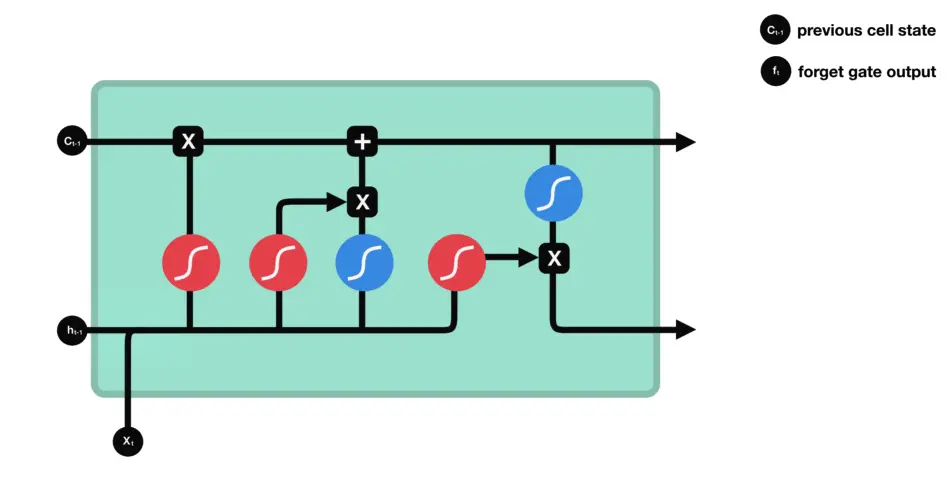
优点:
训练速度比LSTM快。在某些任务中与LSTM表现相当。
缺点:
性能可能略低于LSTM。对于非常复杂的序列可能不够强大。
<code>from keras.layers import GRU
# 创建模型
model = Sequential()
model.add(GRU(50, activation='relu', input_shape=(1, 1)))code>
model.add(Dense(1))
model.compile(optimizer='adam', loss='mse')code>
# 训练模型
model.fit(X_train, y_train, epochs=100, verbose=0)
# 预测
forecast = model.predict(X_test)
print(forecast)
3.4 1D-CNN (Convolutional Neural Networks)
原理:
卷积神经网络通常用于图像处理,但在处理具有空间维度的时间序列数据时也有应用。
优点:
能够自动提取特征。在处理具有局部相关性的数据时效果好。
缺点:
一般需要大量的数据进行训练。可能不适合处理长序列数据。
from keras.layers import Conv1D, MaxPooling1D, Flatten
# 创建模型
model = Sequential()
model.add(Conv1D(filters=64, kernel_size=2, activation='relu', input_shape=(1, 1)))code>
model.add(MaxPooling1D(pool_size=2))
model.add(Flatten())
model.add(Dense(50, activation='relu'))code>
model.add(Dense(1))
model.compile(optimizer='adam', loss='mse')code>
# 训练模型
model.fit(X_train, y_train, epochs=100, verbose=0)
# 预测
forecast = model.predict(X_test)
print(forecast)
3.5 Temporal Convolutional Network (TCN)
详细介绍可以参考我的另一篇博客:时间卷积网络(TCN):序列建模的强大工具(附Pytorch网络模型代码)
原理:
TCN利用了一维卷积层来处理序列数据,它通过堆叠因果卷积和残差链接来捕获长距离依赖,同时保持高效性。因果卷积确保了当前时刻的输出只依赖于过去的输入,这在处理时间序列时非常重要。
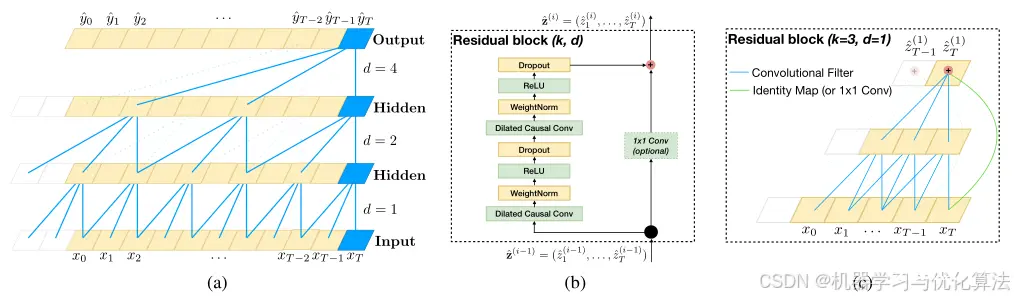
优点:
可以处理长序列数据。并行化计算,相比RNN更快。
缺点:
对于非常长的序列,可能仍然存在信息丢失。参数较多,需要较大的数据集进行训练。
<code>import torch
import torch.nn as nn
from torch.nn.utils import weight_norm
class Chomp1d(nn.Module):
def __init__(self, chomp_size):
super(Chomp1d, self).__init__()
self.chomp_size = chomp_size
def forward(self, x):
return x[:, :, :-self.chomp_size].contiguous()
class TemporalBlock(nn.Module):
def __init__(self, n_inputs, n_outputs, kernel_size, stride, dilation, padding, dropout=0.2):
super(TemporalBlock, self).__init__()
self.conv1 = weight_norm(nn.Conv1d(n_inputs, n_outputs, kernel_size,
stride=stride, padding=padding, dilation=dilation))
self.chomp1 = Chomp1d(padding)
self.relu1 = nn.ReLU()
self.dropout1 = nn.Dropout(dropout)
self.conv2 = weight_norm(nn.Conv1d(n_outputs, n_outputs, kernel_size,
stride=stride, padding=padding, dilation=dilation))
self.chomp2 = Chomp1d(padding)
self.relu2 = nn.ReLU()
self.dropout2 = nn.Dropout(dropout)
self.net = nn.Sequential(self.conv1, self.chomp1, self.relu1, self.dropout1,
self.conv2, self.chomp2, self.relu2, self.dropout2)
self.downsample = nn.Conv1d(n_inputs, n_outputs, 1) if n_inputs != n_outputs else None
self.relu = nn.ReLU()
self.init_weights()
def init_weights(self):
self.conv1.weight.data.normal_(0, 0.01)
self.conv2.weight.data.normal_(0, 0.01)
if self.downsample is not None:
self.downsample.weight.data.normal_(0, 0.01)
def forward(self, x):
out = self.net(x)
res = x if self.downsample is None else self.downsample(x)
return self.relu(out + res)
class TemporalConvNet(nn.Module):
def __init__(self, num_inputs, num_channels, kernel_size=2, dropout=0.2):
super(TemporalConvNet, self).__init__()
layers = []
num_levels = len(num_channels)
for i in range(num_levels):
dilation_size = 2 ** i
in_channels = num_inputs if i == 0 else num_channels[i-1]
out_channels = num_channels[i]
layers += [TemporalBlock(in_channels, out_channels, kernel_size, stride=1, dilation=dilation_size,
padding=(kernel_size-1) * dilation_size, dropout=dropout)]
self.network = nn.Sequential(*layers)
def forward(self, x):
return self.network(x)
3.5 Transformer
原理:
Transformer模型最初设计用于自然语言处理,但同样适用于时间序列预测。它基于自注意力机制,能够并行处理输入序列,从而加速训练和预测。
优点:
可以处理任意长度的序列。并行计算,速度快。
缺点:
对于非常长的序列,内存消耗较大。训练需要大量数据和计算资源。
import math
import torch
import torch.nn as nn
from torch.nn import TransformerEncoder, TransformerEncoderLayer
class PositionalEncoding(nn.Module):
def __init__(self, d_model: int, dropout: float = 0.1, max_len: int = 5000):
super().__init__()
self.dropout = nn.Dropout(p=dropout)
position = torch.arange(max_len).unsqueeze(1)
div_term = torch.exp(torch.arange(0, d_model, 2) * (-math.log(10000.0) / d_model))
pe = torch.zeros(max_len, 1, d_model)
pe[:, 0, 0::2] = torch.sin(position * div_term)
pe[:, 0, 1::2] = torch.cos(position * div_term)
self.register_buffer('pe', pe)
def forward(self, x):
"""
Args:
x: Tensor, shape [seq_len, batch_size, embedding_dim]
"""
x = x + self.pe[:x.size(0)]
return self.dropout(x)
# 定义Transformer编码器层
nhead = 2
nhid = 32 # the dimension of the feedforward network model in nn.TransformerEncoderLayer
nlayers = 2 # the number of nn.TransformerEncoderLayer in nn.TransformerEncoder
dropout = 0.2
# 创建TransformerEncoderLayer实例
encoder_layers = TransformerEncoderLayer(d_model=nhid, nhead=nhead, dropout=dropout)
# 创建TransformerEncoder实例
transformer_encoder = TransformerEncoder(encoder_layers, num_layers=nlayers)
# 创建位置编码实例
pos_encoder = PositionalEncoding(nhid, dropout)
# 假设输入数据shape为(seq_len, batch_size, nhid)
src = torch.rand(100, 1, nhid)
# 应用位置编码
src = pos_encoder(src)
# 传递给TransformerEncoder
output = transformer_encoder(src)
print(output.shape)
参考文献
[1]Box, G. E., Jenkins, G. M., Reinsel, G. C., & Ljung, G. M. (2015). Time series analysis: forecasting and control. John Wiley & Sons.
[2]Hyndman, R. J., & Athanasopoulos, G. (2018). Forecasting: principles and practice. OTexts.
[3]Hochreiter, S., & Schmidhuber, J. (1997). Long short-term memory. Neural computation, 9(8), 1735-1780.
[4]Cho, K., Van Merriënboer, B., Gulcehre, C., Bahdanau, D., Bougares, F., Schwenk, H., & Bengio, Y. (2014). Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv preprint arXiv:1406.1078.
[5]Bai, S., Kolter, J. Z., & Koltun, V. (2018). An empirical evaluation of generic convolutional and recurrent networks for sequence modeling. arXiv preprint arXiv:1803.01271.
[6]Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., ... & Polosukhin, I. (2017). Attention is all you need. In Advances in neural information processing systems (pp. 5998-6008).
[7]Zhou, H., Zhang, S., Peng, J., Zhang, S., Li, J., Xiong, H., & Zhang, W. (2021). Informer: Beyond efficient transformer for long sequence time-series forecasting. In Proceedings of AAAI.
[8]Oreshkin, B. N., Carpov, D., Chapados, N., & Bengio, Y. (2019). N-BEATS: Neural basis expansion analysis for interpretable time series forecasting. arXiv preprint arXiv:1905.10437.
[9]Lim, B., Arık, S. Ö., Loeff, N., & Pfister, T. (2021). Temporal fusion transformers for interpretable multi-horizon time series forecasting. International Journal of Forecasting, 37(4), 1748-1764.
[10]Chen, T., & Guestrin, C. (2016). Xgboost: A scalable tree boosting system. In Proceedings of the 22nd acm sigkdd international conference on knowledge discovery and data mining (pp. 785-794).
[11]Ke, G., Meng, Q., Finley, T., Wang, T., Chen, W., Ma, W., ... & Liu, T. Y. (2017). Lightgbm: A highly efficient gradient boosting decision tree. In Advances in neural information processing systems (pp. 3146-3154).
创作不易,烦请各位观众老爷给个三连,小编在这里跪谢了!

声明
本文内容仅代表作者观点,或转载于其他网站,本站不以此文作为商业用途
如有涉及侵权,请联系本站进行删除
转载本站原创文章,请注明来源及作者。