使用BatchNorm替代LayerNorm可以减少Vision Transformer训练时间和推理时间
deephub 2024-08-22 12:01:02 阅读 52
以Vision Transformer (ViT)的发现为先导的基于transformer的架构在计算机视觉领域引发了一场革命。对于广泛的应用,ViT及其各种变体已经有效地挑战了卷积神经网络(CNN)作为最先进架构的地位。尽管取得了一些成功,但是ViT需要更长的训练时间,并且对于小型到中型输入数据大小,推理速度较慢。因此研究更快训练和推理Vision Transformer就变成了一个重要的方向。
在以前我们都是知道,Batch Normalization(以下简称BN)的方法最早由Ioffe&Szegedy在2015年提出,主要用于解决在深度学习中产生的ICS(Internal Covariate Shift)的问题。若模型输入层数据分布发生变化,则模型在这波变化数据上的表现将有所波动,输入层分布的变化称为Covariate Shift,解决它的办法就是常说的Domain Adaptation
而在transformer上使用Layer Normalization(以下简称LN)的方法,用于解决BN无法很好地处理文本数据长度不一的问题,但是对于VIT来说,图像的块数是固定的,并且长度也是固定的,那么能不能用BN来替代LN呢?

本文我们将详细探讨ViT的一种修改,这将涉及用批量归一化(BatchNorm)替换层归一化(LayerNorm) - transformer的默认归一化技术。ViT有一个仅编码器的架构,transformer编码器由两个不同的模块组成 - 多头自注意力(MHSA)和前馈网络(FFN)。所以我门将讨论这种模型的两个版本。第一个模型将涉及仅在前馈网络中实现BatchNorm层 - 这将被称为ViTBNFFN( 前馈网络中带有BatchNorm的Vision Transformer**)** 。第二个模型将涉及在Vision Transformer的所有地方用BatchNorm替换LayerNorm - 我将这个模型称为ViTBN( 带有BatchNorm的Vision Transformer**)**。因此,模型ViTBNFFN将同时涉及LayerNorm(在MHSA中)和BatchNorm(在FFN中),而ViTBN将仅涉及BatchNorm。
我们将比较这三个模型 - ViTBNFFN、ViTBN和标准ViT - 在MNIST手写数字数据集上的性能。将比较以下指标 - 每个epoch的训练时间、每个epoch的测试/推理时间、训练损失和测试准确率,在两种不同的实验设置中。在第一种设置中,在固定的超参数(学习率和批量大小)选择下比较模型。然后在不同的学习率值下重复该训练,保持所有其他超参数(如批量大小)不变。在第二种设置中,首先使用贝叶斯优化程序找到每个模型的最佳超参数选择,以最大化准确率。然后比较这些优化模型在上述指标方面的性能。
在这两种设置中,模型ViTBNFFN和ViTBN在每个epoch的平均训练时间以及每个epoch的平均推理时间上都实现了超过60%的提升,同时与标准ViT相比,给出了可比(或更优)的准确率。此外,与BatchNorm的模型允许使用更大的学习率,而不影响模型的稳定性。后一个发现与BatchNorm在CNN中部署的一般直觉一致,正如Ioffe和Szegedy的原始论文中指出的那样。
批量归一化:定义和PyTorch实现
让我们简要回顾一下深度神经网络中BatchNorm的基本概念。这个想法最初是由Ioffe和Szegedy在一篇论文中引入的,作为加速卷积神经网络训练的一种方法。假设zᵃᵢ表示深度神经网络给定层的输入,其中a是从a=1,…,Nₛ运行的批次索引,i是从i=1,…,C运行的特征索引。这里Nₛ是一个批次中的样本数,C是生成zᵃᵢ的层的维度。BatchNorm操作然后涉及以下步骤:
1、对于给定特征i,计算大小为Nₛ的批次上的均值和方差,即

2、对于给定特征i,使用上面计算的均值和方差对输入进行归一化,即定义(对于固定的小正数ϵ):
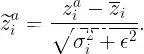
3、最后,对每个特征i的归一化输入进行移位和缩放:

其中a或i索引没有求和,参数(γᵃᵢ,βᵃᵢ)是可训练的。
层归一化(LayerNorm)涉及对固定批次索引a计算特征索引上的均值和方差,然后进行类似的归一化和移位-缩放操作。
PyTorch有一个内置的BatchNorm1d类,它对2d或3d输入执行批量归一化:PyTorch中的BatchNorm1d类。
<code> nn.BatchNorm1d(num_features, eps=1e-05, momentum=0.1, affine=True,
track_running_stats=True)
在通用图像处理任务中,图像通常被分成多个较小的块。输入z然后有一个索引α(除了索引a和i),它标记构成图像的一系列块中的特定块。BatchNorm1d类将输入的第一个索引视为批次索引,第二个索引视为特征索引,其中num_features = C。所以输入是形状为Nₛ × C × N的3d张量,其中N是块的数量。输出张量与输入具有相同的形状。PyTorch还有一个BatchNorm2d类,可以处理4d输入。对于我们来说使用BatchNorm1d类就足够了。
PyTorch中的BatchNorm1d类有一个额外的特性,如果设置track_running_stats = True(这是默认设置),BatchNorm层在训练期间会保持其计算的均值和方差的运行估计,然后在测试期间用于归一化。如果设置选项track_running_stats = False,BatchNorm层不会保持运行估计,而是在测试期间也使用批次统计进行归一化。对于通用数据集,默认设置可能导致训练和测试准确率显著不同,至少在前几个epoch中是这样。但是对于这个数据集,可以明确检查这不是这种情况。所以我们在使用BatchNorm1d类时保持默认设置。
标准Vision Transformer:简要回顾
Vision Transformer(ViT)最初是在论文一幅图像值16 × 16个单词中引入的,用于图像分类任务。让我们简要回顾一下这个模型。下图1显示了这个仅编码器的transformer模型架构的细节,它由三个主要部分组成:嵌入层、transformer编码器和MLP头。

图1. Vision Transformer的架构。
嵌入层将图像分成多个块,并将每个块映射到一个向量。嵌入层的组织如下。可以将2d图像视为形状为H× W × c的实3d张量,其中H、W和c分别是图像的高度、宽度(以像素为单位)和颜色通道数。在第一步中,这样的图像被重新整形为形状为N × dₚ的2d张量,使用大小为p的块,其中N= (H/p) × (W/p)是块的数量,dₚ = p² × c是块维度。作为一个具体的例子,考虑一个28 × 28的灰度图像。在这种情况下,H=W=28,而c=1。如果选择块大小p=7,那么图像被划分为一系列N=4 × 4 = 16个块,块维度为dₚ = 49。
线性层将形状为N × dₚ的张量映射到形状为N × dₑ的张量,其中dₑ被称为嵌入维度。然后通过在前面加上一个可学习的dₑ维向量y₀,将形状为N × dₑ的张量提升为形状为(N+1) × dₑ的张量y。向量y₀表示图像分类上下文中CLS标记的嵌入,我们将在下面解释。然后将另一个形状为(N+1) × dₑ的张量yₑ添加到张量y中 - 这个张量编码了图像的位置嵌入信息。可以选择一个可学习的yₑ或使用固定的1d正弦表示。然后将形状为(N+1) × dₑ的张量z = y+yₑ输入到transformer编码器。图像还会用批次索引标记。所以最后嵌入层的输出是形状为Nₛ × (N+1) × dₑ的3d张量。
transformer编码器(如下图2所示)将形状为Nₛ × (N+1) × dₑ的3d张量zᵢ作为输入,并输出相同形状的张量zₒ。这个张量zₒ依次被输入到MLP头进行最终分类。设z⁰ₒ是沿第二维度对应于zₒ的第一个分量的形状为Nₛ × dₑ的张量。这个张量是我们之前描述的可学习张量y₀的"最终状态",它被添加到编码器的输入张量前面。如果选择使用CLS标记进行分类,MLP头从transformer编码器的输出zₒ中隔离出z⁰ₒ,并将后者映射到Nₛ × n张量,其中n是问题中的类别数。也可以选择执行全局池化,即计算输出张量zₒ在(N+1)个块上给定特征的平均值,得到形状为Nₛ × dₑ的张量zᵐₒ。然后MLP头将zᵐₒ映射到形状为Nₛ × n的2d张量。

图2. Vision Transformer内部transformer编码器的结构。
让我们更详细地讨论transformer编码器的组成部分。如图2所示,它由L个transformer块组成,其中数字L通常被称为模型的深度。每个transformer块又由一个多头自注意力(MHSA)模块和一个MLP模块(也称为前馈网络)组成,如图所示有残差连接。MLP模块由两个隐藏层组成,中间有一个GELU激活层。第一个隐藏层之前还有一个LayerNorm操作。
有了以上的基础知识,我们就可以讨论上面说的ViTBNFFN和ViTBN模型了
带有BatchNorm的Vision Transformer:ViTBNFFN和ViTBN
为了在ViT架构中实现BatchNorm,首先引入了一个针对任务定制的新BatchNorm类,在ViTBNFFN和ViTBN中实现批量归一化操作的Batch_Norm类。
import torch.nn as nn
from einops import rearrange
class Batch_Norm(nn.Module):
def __init__(self, feature_dim):
super().__init__()
self.BN = nn.BatchNorm1d(feature_dim)
def forward(self, x):
x = rearrange(x, 'b n d -> b d n')
x = self.BN(x)
x = rearrange(x, 'b d n -> b n d')
return x
这个新的Batch_Norm类使用了我上面回顾过的BatchNorm1d类(第10行)。重要的修改出现在第13-15行。transformer编码器的输入张量形状为Nₛ × (N+1) × dₑ。在编码器内部的一个通用层,输入是一个形状为Nₛ × (N+1) × D的3d张量,其中D是该层的特征数。为了使用BatchNorm1d类,必须将此张量重塑为Nₛ × D × (N+1)。实现BatchNorm后,需要将张量重塑回Nₛ × (N+1) × D的形状,这样可以让架构的其余部分可以保持不变。这两个重塑操作都是使用einops包中的rearrange函数完成的。
现在可以用以下方式描述带有BatchNorm的模型。首先,可以通过移除前置第一个隐藏层的LayerNorm操作并引入BatchNorm层来修改ViT中transformer编码器的前馈网络。这里选择在第一个隐藏层和GELU激活层之间插入BatchNorm层。这就得到了模型ViTBNFFN。新前馈网络的PyTorch实现如下:
# class FeedForward
class FeedForward(nn.Module):
def __init__(self, dim, hidden_dim, dropout=0.):
super().__init__()
self.Lin1 = nn.Linear(dim,hidden_dim)
self.norm = Batch_Norm(hidden_dim)
self.act = nn.GELU()
self.drop = nn.Dropout(dropout)
self.Lin2 = nn.Linear(hidden_dim, dim)
def forward(self, x):
x = self.Lin1(x)
x = self.norm(x)
x = self.act(x)
x = self.drop(x)
x = self.Lin2(x)
return x
上面的代码就是带有批量归一化的transformer编码器的前馈(MLP)模块。
FeedForward类的构造函数(第7-11行的代码)是非常清晰的。BatchNorm层是由第8行的Batch_Norm类实现的。前馈网络的输入张量形状为Nₛ × (N+1) × dₑ。第一个线性层将其转换为形状为Nₛ × (N+1) × D的张量,其中D = hidden_dim(在代码中也称为mlp_dimension),Batch_Norm类的适当特征维度是D。
接下来是第二个修改,将ViTBNFFN模型中的所有LayerNorm操作替换为由Batch_Norm类实现的BatchNorm操作。这就得到了ViTBN模型。在ViTBNFFN/ViTBN中相对于标准ViT做了几处额外的调整。首先,通过引入一个额外的模型参数,加入了可学习位置编码或固定正弦位置编码的选项。与标准ViT类似,可以选择使用CLS令牌或全局池化进行最终分类的方法。然后用一个更简单的线性头替换了MLP头。有了这些变化,ViTBN类采用以下形式(ViTBNFFN类有类似的形式):
class ViTBN(nn.Module):
def __init__(self, *, image_size, patch_size, num_classes, dim, depth,
heads, mlp_dim, pool, channels, dim_head,
dropout = 0., emb_dropout = 0.,pos_emb):
super().__init__()
image_height, image_width = pair(image_size)
patch_height, patch_width = pair(patch_size)
assert image_height % patch_height == 0 and image_width % patch_width == 0,
'Image dimensions must be divisible by the patch size.'
num_patches = (image_height // patch_height) * (image_width // patch_width)
patch_dim = channels * patch_height * patch_width
assert pool in {'cls', 'mean'}, 'pool type must be either cls (cls token)
or mean (mean pooling)'
assert pos_emb in {'pe1d', 'learn'}, 'pos_emb must be either pe1d or learn'
self.to_patch_embedding = nn.Sequential(
Rearrange('b c (h p1) (w p2) -> b (h w) (p1 p2 c)', p1 = patch_height,
p2 = patch_width),
Batch_Norm(patch_dim),
nn.Linear(patch_dim, dim),
Batch_Norm(dim),
)
self.pos_embedding_1d = posemb_sincos_1d(
h = num_patches + 1, dim = dim,
)
self.pos_embedding_random = nn.Parameter(torch.randn(1, num_patches + 1, dim))
self.cls_token = nn.Parameter(torch.randn(1, 1, dim))
self.dropout = nn.Dropout(emb_dropout)
self.transformer = Transformer(dim, depth, heads, dim_head, mlp_dim, dropout)
self.pool = pool
self.pos_emb = pos_emb
self.to_latent = nn.Identity()
self.linear_head = nn.Linear(dim, num_classes)
def forward(self, x):
x = self.to_patch_embedding(x)
b, n, _ = x.shape
if self.pos_emb == 'pe1d':
pos_emb_1d = repeat(self.pos_embedding_1d, 'n d -> b n d', b = b)
cls_tokens = repeat(self.cls_token, '1 1 d -> b 1 d', b = b)
x = torch.cat((cls_tokens,x), dim=1)
x += pos_emb_1d[:, : n+1]
elif self.pos_emb == 'learn':
pos_emb_random = repeat(self.pos_embedding_random, '1 n d -> b n d', b = b)
cls_tokens = repeat(self.cls_token, '1 1 d -> b 1 d', b = b)
x = torch.cat((cls_tokens,x), dim=1)
x += pos_emb_random[:,: n+1]
x = self.dropout(x)
x = self.transformer(x)
x = x.mean(dim = 1) if self.pool == 'mean' else x[:, 0]
x = self.to_latent(x)
return self.linear_head(x)
上述代码的大部分与标准ViT类非常相似。但是需要注意在第23-28行,在嵌入层中用BatchNorm替换了LayerNorm。在表示ViTBN使用的transformer编码器的Transformer类内部也进行了类似的替换(见第44行)。然后添加了一个新的超参数"pos_emb",它接受字符串值’pe1d’或’learn’。在第一种情况下,使用固定的1d正弦位置嵌入,而在第二种情况下使用可学习的位置嵌入。在forward函数中,第一个选项在第62-66行实现,而第二个选项在第68-72行实现。超参数"pool"接受字符串值’cls’或’mean’,分别对应于最终分类的CLS令牌或全局池化。ViTBNFFN类可以用类似的方式编写。
ViTBN模型(类似地,ViTBNFFN)可以如下使用:
def get_model():
model = ViTBN(
image_size = 28,
patch_size = 7,
num_classes = 10,
channels =1,
dim = 64,
depth = 6,
heads = 8,
dim_head = 64,
mlp_dim = 128,
pool = 'cls' or 'mean',
dropout = 0.0,
emb_dropout = 0.0,
pos_emb ='learn' or 'pe1d'
)
return model
上面代码是对28 × 28图像使用ViTBN。
在这个特定情况下,有输入维度image_size = 28,这意味着H = W = 28。patch_size = p =7意味着patches的数量为N = 16。颜色通道数为1,patch维度为dₚ =p²= 49。分类问题中的类别数由num_classes给出。模型中的参数dim = 64是嵌入维度dₑ。编码器中transformer块的数量由depth = L =6给出。参数heads和dim_head分别对应于编码器MHSA模块中自注意力头的数量和每个头的(共同)维度。参数mlp_dim是MLP或前馈模块的隐藏维度。参数dropout是transformer编码器的单一dropout参数,同时出现在MHSA和MLP模块中,而emb_dropout是与嵌入层相关的dropout参数。
实验1:在固定超参数下比较模型
上面我们完成了带有BatchNorm的模型后,可以开始第一个数值实验。BatchNorm使深度神经网络更快地收敛,从而加快训练和推理速度。它还允许使用相对较大的学习率训练CNN而不会引入不稳定性。因为预计它会起到正则化器的作用,消除对dropout的需求。我们第一个实验的主要动机是了解这些说法如何转化到带有BatchNorm的Vision Transformer。实验包括以下步骤:
对于给定的学习率,我将在MNIST手写图像数据集上训练ViT、ViTBNFFN和ViTBN模型,总共30个epoch。在这个阶段,不使用任何图像增强。在每个训练epoch之后对验证数据进行一次测试。对于给定的模型和给定的学习率,在给定epoch中测量以下数量:训练时间、训练损失、测试时间和测试准确率。对于固定的学习率,这将生成四个图表,每个图表绘制这四个数量中的一个作为三个模型的epoch函数。然后可以使用这些图表来比较模型的性能。特别是想比较标准ViT与带有BatchNorm的模型的训练和测试时间,以检查在任何情况下是否有显著的加速。对三个代表性学习率l = 0.0005、0.005和0.01执行步骤1和步骤2中的操作,同时保持所有其他超参数不变。
在分析过程中,使用CrossEntropyLoss()作为损失函数和Adam优化器,所有epoch的训练和测试批量大小分别固定为100和5000。并将所有dropout参数设置为零确保不进行dropout操作,同时也不考虑任何学习率衰减。其他超参数在上面的代码中已经给出了 - 使用CLS令牌进行分类,这对应于设置pool = ‘cls’,以及可学习的位置嵌入,这对应于设置pos_emb = ‘learn’。
首先是train_model函数,它将用于给定超参数选择的模型训练和测试:
from datetime import datetime
def train_model(model,train_loader,validation_loader, validation_dataset,
optimizer,criterion,n_epochs):
#global variable
N_test=len(validation_dataset)
accuracy_list=[]
cost_list=[]
loss_list=[]
dur_list_train=[]
dur_list_val = []
COST=0.
correct=0.
delta_train=0
delta_val=0
# training the model
for epoch in range(n_epochs):
COST=0.
t0 = datetime.now()
for x, y in train_loader:
optimizer.zero_grad()
model.train()
z = model(x)
loss = criterion(z, y)
loss.backward()
optimizer.step()
COST+=loss.data.item()
cost_list.append(COST)
delta_train= datetime.now() - t0
dur_list_train.append(delta_train.total_seconds())
# testing
correct = 0.
t1 = datetime.now()
for x_test, y_test in validation_loader:
model.eval()
z = model(x_test)
_, yhat = torch.max(z, 1)
correct += (yhat == y_test).sum().item()
accuracy = correct / N_test
accuracy_list.append(accuracy)
delta_val=datetime.now() - t1
dur_list_val.append(delta_val.total_seconds())
return cost_list, accuracy_list, dur_list_train, dur_list_val
train_model函数为每个epoch返回四个数量 - 训练损失(cost_list)、测试准确率(accuracy_list)、训练时间(秒)(dur_list_train)和测试时间(秒)(dur_list_val)。第19-32行的代码给出了函数的训练模块,而第35-45行给出了测试模块。该函数允许在每个训练epoch之后对模型进行一次测试。
接下来,需要定义一个函数,该函数将下载MNIST数据,将其拆分为训练数据集和验证数据集,并将图像转换为torch张量(不进行任何增强):
def get_datasets() :
data_transform = transforms.Compose([
transforms.Resize(28),
transforms.ToTensor()
])
#Load training data
train_dataset = dsets.MNIST(root='./data', train=True, download=True, transform= data_transform)code>
#Load validation data
validation_dataset = dsets.MNIST(root='./data', train=False, download=True, transform= data_transform)code>
return train_dataset, validation_dataset
我们使用MLFlow进行训练
import os
import mlflow
mlflow.set_tracking_uri(os.getenv("MLFLOW_TRACKING_URI"))
if __name__ == "__main__":
mlflow.pytorch.autolog()
# specifying training parameters
learning_rate = 0.0005
n_epochs = 30
criterion = nn.CrossEntropyLoss()
# mlflow run
with mlflow.start_run(experiment_id=):
train_dataset, validation_dataset = get_datasets()
model = get_model()
optimizer = torch.optim.Adam(model.parameters(), lr = learning_rate)
train_loader = torch.utils.data.DataLoader(dataset=train_dataset,
batch_size=100,shuffle=True)
validation_loader = torch.utils.data.DataLoader(dataset=validation_dataset,
batch_size=5000, shuffle=True)
cost_list, accuracy_list, dur_list_train, dur_list_val = train_model(model,
train_loader,
validation_loader,
validation_dataset,
optimizer,
criterion,
n_epochs)
# logging parameters
mlflow.log_params({
"learning_rate": learning_rate,
"epochs": n_epochs
})
# logging metrics
for i in range(n_epochs):
mlflow.log_metrics(
{
"training_loss": cost_list[i],
"validation_accuracy": accuracy_list[i],
"training_time": dur_list_train[i],
"validation_time": dur_list_val[i]
},step = i+1
)
print("done.")
这是标准的训练过程,可以略过,如果你像详细了解,请看一些重要部分的解释
第11-13行分别指定学习率、epoch数和损失函数。
第16-33行指定了训练和测试的各种细节。代码块7中的get_datesets()函数下载MNIST数字的训练和验证数据集,并使用前面代码中定义的get_model()函数指定模型。对于后者,我们设置pool = 'cls’和pos_emb = ‘learn’。
在第20行定义了优化器,并在第21-24行指定了训练和验证数据加载器,包括各自的批量大小。第25-26行指定了代train_model函数的输出 - 四个列表,每个列表都有n_epoch个条目。第16-24行指定了train_model函数的各种参数。
在第37-40行,指定了将为实验的给定运行记录的参数,对于我们的实验,这些参数是学习参数和epoch数。
第44-52行构成了代码的最重要部分,其中指定了要记录的指标,即上面提到的四个列表。默认情况下,函数mlflow.log_metrics()不会记录列表。如果我们简单地使用mlflow.log_metrics({generic_list}),那么实验将只记录最后一个epoch的输出。所以我们使用for循环多次调用该函数。
训练完成后,我们可以深入研究实验结果,这些结果基本上总结在下面的图中。每个图呈现了四个图表,对应于每个epoch的训练时间(左上)、每个epoch的测试时间(右上)、训练损失(左下)和测试准确率(右下),用于三个模型的固定学习率。图3、4和5分别对应于学习率l=0.0005、l=0.005和l=0.01。为了进行对比,我们定义了一些自己的对比指标:
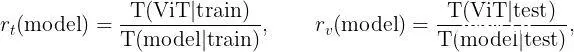
其中T(model|train)和T(model|test)分别是我们实验中给定模型的每个epoch的平均训练和测试时间。这些比率大致衡量了由于集成BatchNorm而导致的Vision Transformer的加速。我们将始终训练和测试模型相同数量的epoch - 因此可以分别根据上述比率定义每个epoch平均训练和测试时间的百分比增益:
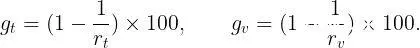
下面从最小的学习率l=0.0005开始,这对应于下图3。在这种情况下,标准ViT比其他模型在较少的epoch数内收敛。经过30个epoch后,标准ViT具有较低的训练损失和略高的准确率(98.2%),相比之下ViTBNFFN(97.8%)和ViTBN(~97.1%) - 见右下图。但是ViT的训练时间和测试时间比ViTBNFFN/ViTBN高出2倍以上。从图表中可以读出rₜ和rᵥ的比率:rₜ(ViTBNFFN) = 2.7,rᵥ(ViTBNFFN)= 2.6,rₜ(ViTBNFFN) = 2.5,和rᵥ(ViTBN)= 2.5,其中rₜ,rᵥ如上定义。所以对于给定的学习率,由于BatchNorm导致的训练和推理速度增益是显著的 - 大约为60%。精确的百分比增益列在表1中。
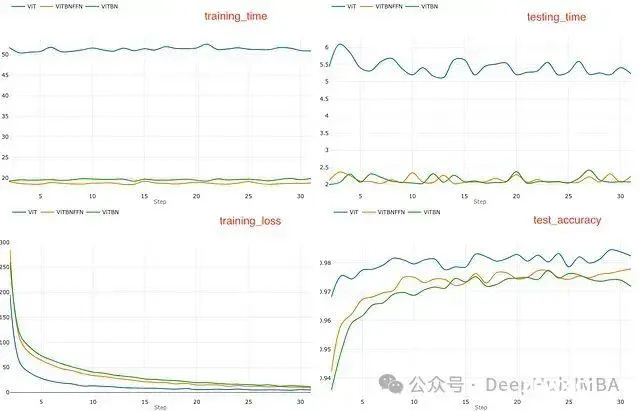
图3. 学习率l = 0.0005的图表。
下一步将学习率增加到l=0.005并重复实验,这产生了图4中的一组图表。

图4. 学习率l=0.005的图表。
对于学习率 l=0.005,标准 ViT 在收敛速度方面似乎没有任何优势。并且ViT 的训练时间和测试时间仍然比 ViTBNFFN/ViTBN 更长。通过对比图 3 和图 4 左上角的图表可以看出,ViT 的训练时间显著增加,而 ViTBNFFN 和 ViTBN 的训练时间大致保持不变。这意味着在这种情况下,训练时间的提升更为显著。并且比较图 3 和图 4 右上角的图表,可以看出测试速度的提升大致相同。从图 4 顶行的图表中可以再次读取比率 rₜ 和 rᵥ:rₜ (ViTBNFFN) = 3.6,rᵥ (ViTBNFFN)=2.5,rₜ (ViTBN) = 3.5 和 rᵥ (ViTBN)= 2.5。这里的 rₜ 比率比较小学习率的情况下更大,而 rᵥ 比率保持大致相同。这导致训练时间的百分比增益更高(70%),而推理时间的增益(60%)大致保持不变。
最后,让我们将学习率进一步提高到 l=0.01 并重复实验,得到图 5 中的一组图表。

图 5. 学习率 l=0.01 的图表。
ViT 在几个 epoch 后变得不稳定,从图 5 中的 training_loss 图可以看出,在第 15 个 epoch 附近开始出现非收敛行为。test_accuracy 图也证实了这一点,ViT 的准确率在第 15 个 epoch 左右急剧下降。但是ViTBNFFN 和 ViTBN 模型保持稳定,并在 30 个 epoch 训练结束时达到超过 97% 的准确率。在这种情况下,ViT 的训练时间更长,并且波动很大。对于 ViTBNFFN,训练时间有明显增加,而对于 ViTBN 则大致保持不变 - 见左上图。就训练比率 rₜ 而言rₜ (ViTBNFFN) = 2.7 和 rₜ(ViTBN)=4.3。第一个比率低于前一种情况下发现的值。这是由于 ViTBNFFN 的训练时间较长,抵消了 ViT 训练时间的增加。第二个比率显著更高是因为 ViTBN 的训练时间大致保持不变。这种情况下的测试比率 rᵥ - rᵥ (ViTBNFFN)=2.6 和 rᵥ (ViTBN)= 2.7 - 显示出微小的增加。
下表 1 总结了不同学习率下训练和推理时间的增益 - gₜ 和 gᵥ。

更直观地展示每个模型的训练时间如何随学习率变化也很有趣。下图 6 中的三组图表分别显示了 ViT、ViTBNFFN 和 ViTBN 的这种变化。模型_i 中的下标 i=1,2,3 分别对应给定模型的三个学习率 l= 0.0005、0.005 和 0.01。

图 6. 显示每个模型的每个 epoch 训练时间如何随学习率变化的图表。下标 1,2,3 分别对应 l=0.0005、0.005 和 0.01。
可以看到ViT 的训练时间随学习率的变化最为显著(顶部图)。另一方面,随着我们改变学习率,ViTBN 的训练时间大致保持不变(底部图)。对于 ViTBNFFN,只有在相对较大的学习率值(~0.01)时,变化才变得显著(中间图)。
实验 2:比较优化后的模型
现在让我们设置实验,比较优化后模型的性能:
首先进行贝叶斯优化,以确定每个模型的最佳超参数集 - 学习参数和批量大小。给定三个优化后的模型,对每个模型进行 30 个 epoch 的训练和测试,并且特别记录每个 epoch 的训练和测试/推理时间。
我们使用准确率作为优化指标,并将优化过程限制在 20 次迭代。我们还需要指定每种情况下搜索将在其中进行的超参数范围。根据经验,将ViT 的学习参数范围设置在[1e-5, 1e-3],而 ViTBNFFN 和 ViTBN 的范围是 [1e-5, 1e-2]。对于所有三个模型,批量大小范围是 [20, 120]。
该过程的结果是每个模型的一组优化超参数。我们在表 2 中总结了它们。

表 2. 进行贝叶斯优化得到的每个模型的优化超参数。
对于每个模型,可以绘制准确率如何随迭代次数收敛的图表。作为说明性示例,我们在图 7 中展示了 ViTBNFFN 的收敛图。

现在可以开始第 2 步 - 使用优化后的超参数对每个模型进行 30 个 epoch 的训练和测试。图 8 中的四个图表总结了 30 个 epoch 训练和测试后模型指标的比较。
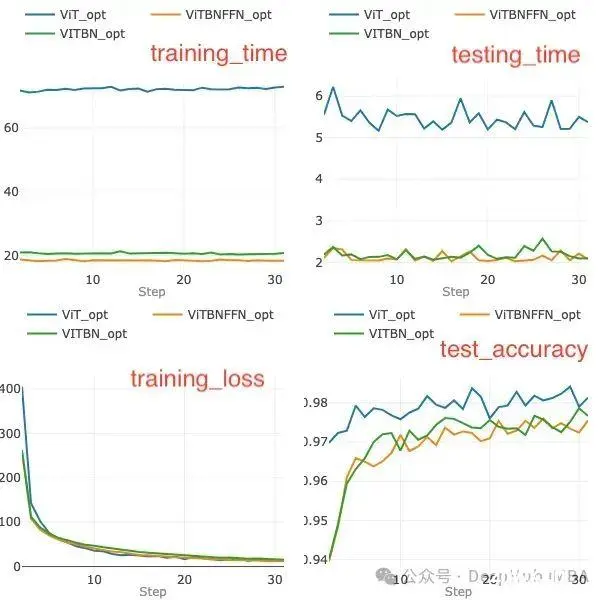
图 8. 比较在 MNIST 数据上训练和测试 30 个 epoch 后优化模型的指标。
在 30 个 epoch 结束时,ViT、ViTBNFFN 和 ViTBN 模型分别达到 98.1%、97.6% 和 97.8% 的准确率。ViT 相比 ViTBNFFN 和 ViTBN 在更少的 epoch 数内收敛。
从图 8 顶行的两个图表中,可以很容易地看出具有 BatchNorm 的模型在每个 epoch 的训练和推理速度都显著更快。对于 ViTBNFFN,可以从上述数据计算出比率 rₜ 和 rᵥ:rₜ (ViTBNFFN) = 3.9 和 rᵥ(ViTBNFFN)= 2.6,而对于 ViTBN,我们有 rₜ (ViTBN) = 3.5 和 rᵥ(ViTBN)= 2.5。下表 3 总结了每个 epoch 平均训练时间和每个 epoch 平均推理时间的增益(分别为 gₜ 和 gᵥ)。

表 3. ViTBNFFN 和 ViTBN 相对于标准 ViT 的每个 epoch 训练时间和推理时间增益。
回顾
让我们现在对我们的工作进行一个快速总结:
固定学习率下的训练和测试速度增益: 相对于 ViT,ViTBNFFN 和 ViTBN 的每个 epoch 平均训练时间显著加快。在这里探索的学习率范围内,增益 gₜ 始终 >~ 60%,但可能根据学习率和模型的不同而显著变化,这从表 1 中可以明显看出。对于每个 epoch 的平均测试时间,也有显著的增益(~60%),但这在整个学习率范围内对两个模型而言大致保持不变。优化模型的训练和测试速度增益: ViTBNFFN 和 ViTBN 的每个 epoch 平均训练时间增益都超过 70%,而推理时间的增益略高于 60% - gₜ 和 gᵥ 的精确值总结在表 3 中。优化后的 ViT 模型比带有 BatchNorm 的模型收敛更快。BatchNorm 和更高的学习率: 对于较小的学习率(~ 0.0005),所有三个模型都是稳定的,ViT 相比 ViTBNFFN/ViTBN 收敛更快。对于中等学习率(~ 0.005),三个模型的收敛性非常相似。对于更高的学习率(~ 0.01),ViT 变得不稳定,而 ViTBNFFN/ViTBN 模型保持稳定,准确率与中等学习率的情况相当,我们的发现证实了一般的预期,即在架构中集成 BatchNorm 允许使用更高的学习率。训练时间随学习率的变化: 对于 ViT,随着学习率的提高,每个 epoch 的平均训练时间大幅增加,而对于 ViTBNFFN,这种增加要小得多。另外对于 ViTBN,训练时间的变化最小。换句话说,对于 ViTBN,训练时间对学习率变化最稳定。
总结
在本文中,我介绍了两个在 ViT 类型架构中集成 BatchNorm 的模型 - 其中一个在前馈网络中部署 BatchNorm(ViTBNFFN),而另一个则在所有地方用 BatchNorm 替换 LayerNorm(ViTBN)。从上面讨论的数值实验中,我们得到了2个结果:
首先,带有 BatchNorm 的模型显著加快了 ViT 的训练和推理速度。对于 MNIST 数据集,在考虑的学习率范围内,每个 epoch 的训练和测试时间至少加快了 60%。
其次,带有 BatchNorm 的模型允许在训练期间使用更大的学习率,而不会使模型变得不稳定。
最后在本文中注意力集中在标准 ViT 架构上。但是显然可以将讨论扩展到其他基于 transformer 的计算机视觉架构。比如姚等人已经解决了在 DeiT(Data efficient image Transformer)和 Swin Transformer 中集成 BatchNorm 的问题。
所以说对于知识的掌握,我们不应当局限于死记硬背。知识不仅仅是简单的记忆和重复,更重要的是理解其背后的原理和应用。每一种情况都有其独特的背景和要求,因此我们应该根据实际情况灵活运用所学的知识,而不是一味地追求机械记忆。
本文完整代码:
https://avoid.overfit.cn/post/94913313e55b4f3db99d7b07aec57e11
作者:Anindya Dey, PhD
声明
本文内容仅代表作者观点,或转载于其他网站,本站不以此文作为商业用途
如有涉及侵权,请联系本站进行删除
转载本站原创文章,请注明来源及作者。