互信息

互信息用于表示两个随机变量相互依赖的程度。随机变量 \(X\) 和 \(Y\) 的互信息定义为

\[\begin{aligned}

I(X, Y)

& = \mathrm{KL}[p(\boldsymbol{x}, \boldsymbol{y}) \parallel p(\boldsymbol{x})p(\boldsymbol{y})] \\

& = \mathbb{E}_{(\boldsymbol{x}, \boldsymbol{y}) \sim p(\boldsymbol{x}, \boldsymbol{y})} \left[\log\frac{p(\boldsymbol{x}, \boldsymbol{y})}{p(\boldsymbol{x})p(\boldsymbol{y})}\right],

\end{aligned}

\]

其中 \(p(\boldsymbol{x}, \boldsymbol{y})\) 表示 \(X\) 和 \(Y\) 的联合概率密度，\(p(\boldsymbol{x})\) 和 \(p(\boldsymbol{y})\) 分别表示 \(X\) 和 \(Y\) 的边缘概率密度。

互信息是一个非负的量，当且仅当 \(X\) 和 \(Y\) 相互独立时（此时 \(p(\boldsymbol{x}, \boldsymbol{y}) = p(\boldsymbol{x})p(\boldsymbol{y})\) 恒成立）取到最小值 \(0\)。

在机器学习中，联合分布 \(p(\boldsymbol{x}, \boldsymbol{y})\) 通常是难以得到的，因此通常会用贝叶斯公式转换一下，使用以下两种形式的互信息：

\[\begin{aligned}

I(X, Y)

& = \mathbb{E}_{(\boldsymbol{x}, \boldsymbol{y}) \sim p(\boldsymbol{x}, \boldsymbol{y})} \left[\log\frac{p(\boldsymbol{x}, \boldsymbol{y})}{p(\boldsymbol{x})p(\boldsymbol{y})}\right] \\

& = \mathbb{E}_{(\boldsymbol{x}, \boldsymbol{y}) \sim p(\boldsymbol{x}, \boldsymbol{y})} \left[\log\frac{p(\boldsymbol{x}|\boldsymbol{y})}{p(\boldsymbol{x})}\right] \\

& = \mathbb{E}_{(\boldsymbol{x}, \boldsymbol{y}) \sim p(\boldsymbol{x}, \boldsymbol{y})} \left[\log\frac{p(\boldsymbol{y}|\boldsymbol{x})}{p(\boldsymbol{y})}\right].

\end{aligned}

\]

信息瓶颈

令随机变量 \(X\) 表示输入数据，\(Z\) 表示编码后的特征，\(Y\) 表示标签。信息瓶颈 (Information Bottleneck) 理论认为，神经网络的优化存在两阶段性：

1. 快速拟合阶段：增加 \(I(Z, X)\)。
2. 压缩阶段：减少 \(I(Z, X)\) 并增加 \(I(Z, Y)\)。

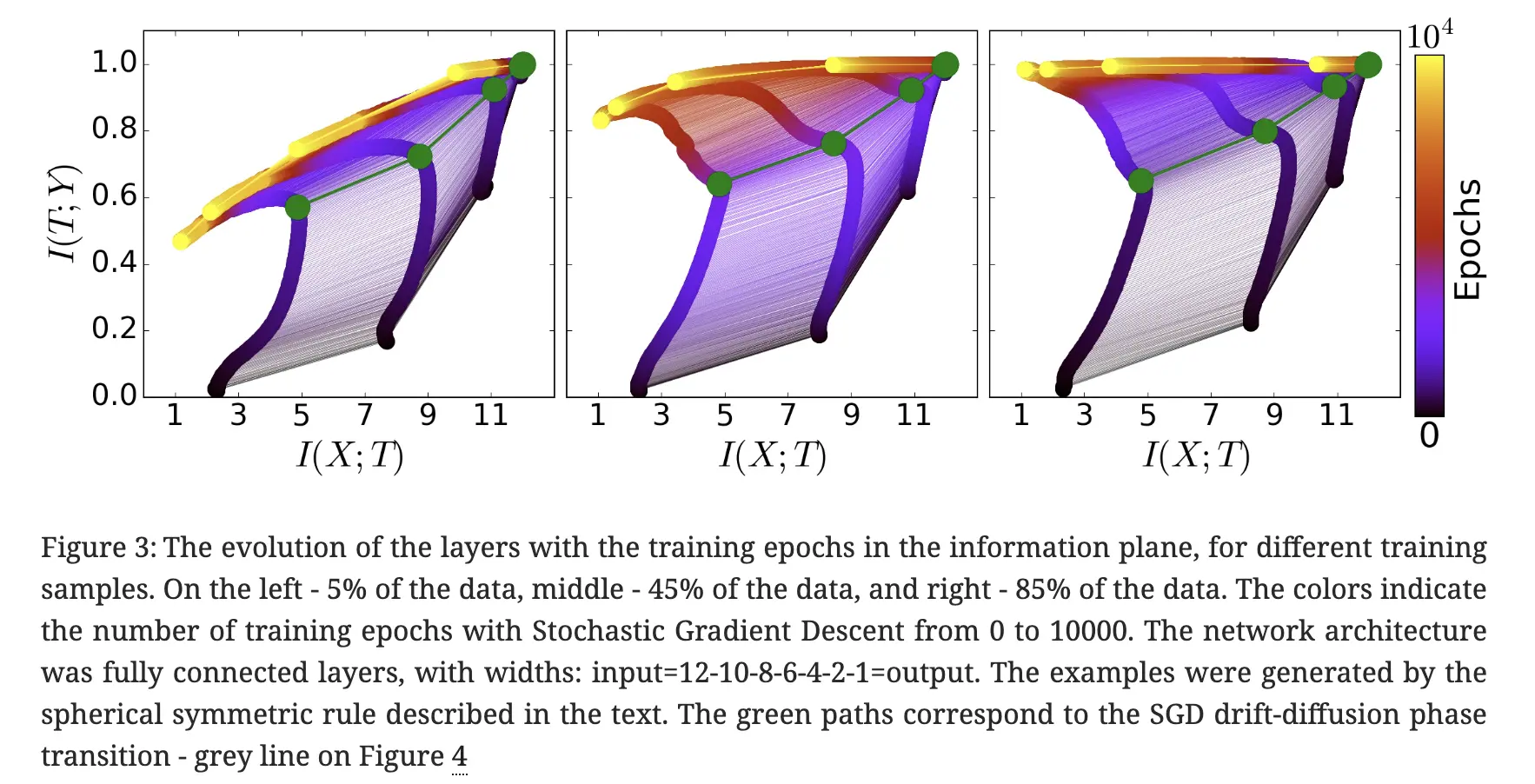
上面这幅插图可视化了神经网络训练过程中互信息的变化轨迹，横轴表示特征与输入的互信息 \(I(Z, X)\)，纵轴表示特征与标签的互信息 \(I(Z, Y)\)（图中用 \(T\) 表示特征），从紫色到黄色表示从 0 epoch 到 10000 epoch。从图中可见，随着训练的进行，\(I(Z, X)\) 有一个先增大再减小的过程。

插图出自论文 [1703.00810] Opening the Black Box of Deep Neural Networks via Information。参考阅读：Anatomize Deep Learning with Information Theory | Lil'Log。

那么能不能利用这个现象对神经网络的训练进行正则化呢，于是有人提出了变分信息瓶颈 (Variational Information Bottleneck, VIB) 方法，优化的目标为：

\[\max_{\boldsymbol{\boldsymbol{\theta}}} I(Z, Y; \boldsymbol{\theta}) - \beta I(Z, X; \boldsymbol{\theta}).

\]

我们希望 \(Z\) 能尽量准确地预测 \(Y\)，同时尽量地遗忘 \(X\) 中的信息。换句话说，我们希望 \(Z\) 遗忘 \(X\) 中的冗余信息，只保留那些对预测 \(Y\) 有用的信息。这里的最小化 \(I(Z, X; \boldsymbol{\theta})\) 起到了正则化的效果。

遗憾的是，从高维数据中直接估计互信息是很困难的，变分信息瓶颈的解决思路是通过变分近似实现对互信息的估计。

最小化 I(Z, X)

使用如下形式的互信息 \(I(Z, X)\)：

\[I(Z, X; \boldsymbol{\theta}) = \mathbb{E}_{(\boldsymbol{x}, \boldsymbol{z}) \sim p(\boldsymbol{x}, \boldsymbol{z})}\left[\log\frac{p(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\theta})}{p(\boldsymbol{z})}\right] \\

\]

注意到这里需要 \(p(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\theta})\)，一种比较方便的处理方法是像 VAE 那样使用概率编码器 (probabilistic encoder)，而不是传统的确定性编码器 (deterministic encoder)，即 \(X \mapsto Z\) 是一个随机函数而不是传统的确定性函数。参考 VAE 中的做法，我们将 \(p(\boldsymbol{z}|\boldsymbol{x})\) 预定义为参数化的高斯分布，并用神经网络输出这个高斯分布的参数：

\[p(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\theta}) := N(\boldsymbol{z}; \boldsymbol{\mu}(\boldsymbol{x}; \boldsymbol{\theta}), \boldsymbol{\sigma}^2(\boldsymbol{x}; \boldsymbol{\theta})\boldsymbol{I}).

\]

解决了 \(p(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\theta})\)，接下来的问题是如何求解 \(p(\boldsymbol{z})\)。可能会想到采样估计的办法，即蒙特卡洛 (Monte Carlo, MC) 估计：

\[\begin{aligned}

p(\boldsymbol{z})

& = \int_{\boldsymbol{x}} p(\boldsymbol{x})p(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\theta})\mathrm{d}\boldsymbol{x} \\

& = \mathbb{E}_{\boldsymbol{x} \sim p(\boldsymbol{x})}[p(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\theta})] \\

& \approx \frac{1}{N}\sum_{i=1}^N p(\boldsymbol{z}|\boldsymbol{x}_i; \boldsymbol{\theta}), \quad \boldsymbol{x}_i \sim p(\boldsymbol{x}).

\end{aligned}

\]

但是论文作者并没有使用这种方法，可能是认为在这里用 MC 估计的方差太大了，需要大量采样才能估得准，效率太低。为了估计期望 \(\mathbb{E}_{(\boldsymbol{x}, \boldsymbol{z}) \sim p(\boldsymbol{x}, \boldsymbol{z})}\left[\log\frac{p(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\theta})}{p(\boldsymbol{z})}\right]\)，就先要从 \(p(\boldsymbol{x})\) 中采样 \(\boldsymbol{x}\)，然后从 \(p(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\theta})\) 中采样 \(\boldsymbol{z}\)。更麻烦的是方括号内的函数值也无法直接解析求解，需要先采样估计出 \(p(\boldsymbol{z})\) 才能计算。采样估计的过程太多，估计的方差自然会大。

变分信息瓶颈，顾名思义，就是通过变分近似的方法来解决无法获得 \(p(\boldsymbol{z})\) 的问题。假如有一个形式已知的无参分布 \(q(\boldsymbol{z})\)，它跟 \(p(\boldsymbol{z})\) 非常接近，那我们用这个 \(q(\boldsymbol{z})\) 替换掉公式里的 \(p(\boldsymbol{z})\)，不就能近似地计算互信息 \(I(Z, X)\) 吗？这里不妨将 \(q(\boldsymbol{z})\) 定义为标准高斯分布，即 \(q(\boldsymbol{z}) := N(\boldsymbol{z}, \boldsymbol{0}, \boldsymbol{I})\)。

接下来需要证明这种替换是有道理的，参考 VAE 中推导的经验，我们尝试用 \(q(\boldsymbol{z})\) 替换 \(p(\boldsymbol{z})\)，并尝试把额外的部分凑出一个 KL：

\[\begin{aligned}

I(Z, X; \boldsymbol{\theta})

& = \mathbb{E}_{(\boldsymbol{x}, \boldsymbol{z}) \sim p(\boldsymbol{x}, \boldsymbol{z})}\left[\log\frac{p(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\theta})}{p(\boldsymbol{z})}\right] \\

& = \mathbb{E}_{(\boldsymbol{x}, \boldsymbol{z}) \sim p(\boldsymbol{x}, \boldsymbol{z})}\left[\log\frac{p(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\theta})}{q(\boldsymbol{z})}\frac{q(\boldsymbol{z})}{p(\boldsymbol{z})}\right] \\

& = \mathbb{E}_{(\boldsymbol{x}, \boldsymbol{z}) \sim p(\boldsymbol{x}, \boldsymbol{z})}\left[\log\frac{p(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\theta})}{q(\boldsymbol{z})}\right] + \mathbb{E}_{(\boldsymbol{x}, \boldsymbol{z}) \sim p(\boldsymbol{x}, \boldsymbol{z})}\left[\log\frac{q(\boldsymbol{z})}{p(\boldsymbol{z})}\right]

\end{aligned}

\]

对于第一项，\(p(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\theta})\) 和 \(q(\boldsymbol{z})\) 都有解析式，因此方括号内的函数可以算出解析解。利用 \(p(\boldsymbol{x}, \boldsymbol{z}) = p(\boldsymbol{x})p(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\theta})\)，可以把第一项写得好看些：

\[\begin{aligned}

\mathbb{E}_{(\boldsymbol{x}, \boldsymbol{z}) \sim p(\boldsymbol{x}, \boldsymbol{z})}\left[\log\frac{p(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\theta})}{q(\boldsymbol{z})}\right]

& = \iint p(\boldsymbol{x})p(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\theta})\log\frac{p(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\theta})}{q(\boldsymbol{z})} \mathrm{d}\boldsymbol{z}\mathrm{d}\boldsymbol{x} \\

& = \int_x p(\boldsymbol{x}) \int_z p(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\theta})\log\frac{p(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\theta})}{q(\boldsymbol{z})} \mathrm{d}\boldsymbol{z}\mathrm{d}\boldsymbol{x} \\

& = \mathbb{E}_{\boldsymbol{x} \sim p(\boldsymbol{x})}[\mathrm{KL}[p(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\theta}) \parallel q(\boldsymbol{z})]] \overset{\text{def}}{=} R(Z, X; \boldsymbol{\theta}) \\

& \approx \frac{1}{N} \cdot \mathrm{KL}[p(\boldsymbol{z}|x_i; \boldsymbol{\theta}) \parallel q(\boldsymbol{z})], \quad x_i \sim p(\boldsymbol{x}).

\end{aligned}

\]

这个 \(R(Z, X; \boldsymbol{\theta}) := \mathbb{E}_{\boldsymbol{x} \sim p(\boldsymbol{x})}[\mathrm{KL}[p(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\theta}) \parallel q(\boldsymbol{z})]]\) 常常被称为 rate，也就是率失真理论里的率。Rate 这一项是可以用 mini-batch 梯度下降来优化的，具体来说，从训练集中采样一批样本 \(\boldsymbol{x}_1, \ldots, \boldsymbol{x}_N\)，最小化每个 \(\boldsymbol{x}_i\) 的 \(\mathrm{KL}[p(\boldsymbol{z}|\boldsymbol{x}_i; \boldsymbol{\theta}) \parallel q(\boldsymbol{z})]\) 即可。由于两个分布都是高斯分布，因此这里的 KL 有解析解：

\[\begin{aligned}

& \mathrm{KL}[p(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\theta}) \parallel q(\boldsymbol{z})] \\

& = \mathrm{KL}[N(\boldsymbol{\mu}(\boldsymbol{x}), \boldsymbol{\sigma}^2(\boldsymbol{x})\boldsymbol{I}), N(\boldsymbol{0}, \boldsymbol{I})] \\

& = \sum_{j=1}^J \mathrm{KL}[N(\mu_j, \sigma^2_j) \parallel N(0, 1)] \\

& = \sum_{j=1}^J \frac{1}{2}(-\log\sigma^2_j - 1 + \mu^2_j + \sigma^2_j).

\end{aligned}

\]

详细的推导过程可参考从极大似然估计到变分自编码器 - VAE 公式推导中“KL 散度的解析解”这一节。相比原来的形式，“写得好看”之后的好处在于：函数对 \(\boldsymbol{z}\) 的积分可以解析地求解，这样一来，用 MC 估计 \(R(Z, X; \boldsymbol{\theta})\) 时，只需要从 \(p(\boldsymbol{x})\) 中采样 \(\boldsymbol{x}\)，无需再从 \(p(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\theta})\) 中采样 \(\boldsymbol{z}\)，减少了采样带来的误差。

对于第二项，注意到期望方括号中的函数跟 \(\boldsymbol{x}\) 没关系，因此：

\[\begin{aligned}

\mathbb{E}_{(\boldsymbol{x}, \boldsymbol{z}) \sim p(\boldsymbol{x}, \boldsymbol{z})}\left[\log\frac{q(\boldsymbol{z})}{p(\boldsymbol{z})}\right]

& = \mathbb{E}_{\boldsymbol{z} \sim p(\boldsymbol{z})}\left[\log\frac{q(\boldsymbol{z})}{p(\boldsymbol{z})}\right] \\

& = -\mathbb{E}_{\boldsymbol{z} \sim p(\boldsymbol{z})}\left[\log\frac{p(\boldsymbol{z})}{q(\boldsymbol{z})}\right] \\

& = -\mathrm{KL}[p(\boldsymbol{z}) \parallel q(\boldsymbol{z})],

\end{aligned}

\]

如果要详细证明一下的话就是：

\[\begin{aligned}

\mathbb{E}_{(\boldsymbol{x}, \boldsymbol{z}) \sim p(\boldsymbol{x}, \boldsymbol{z})}\left[\log\frac{q(\boldsymbol{z})}{p(\boldsymbol{z})}\right]

& = \iint p(\boldsymbol{x}, \boldsymbol{z})\log\frac{q(\boldsymbol{z})}{p(\boldsymbol{z})} \mathrm{d}\boldsymbol{z}\mathrm{d}\boldsymbol{x} \\

& = \int_{\boldsymbol{z}}\log\frac{q(\boldsymbol{z})}{p(\boldsymbol{z})}\left(\int_{\boldsymbol{x}} p(\boldsymbol{z}, \boldsymbol{x})\mathrm{d}\boldsymbol{x}\right)\mathrm{d}\boldsymbol{z} \\

& = \int_{\boldsymbol{z}}\log\frac{q(\boldsymbol{z})}{p(\boldsymbol{z})}p(\boldsymbol{z})\mathrm{d}\boldsymbol{z} \\

& = \mathbb{E}_{\boldsymbol{z} \sim p(\boldsymbol{z})}\left[\log\frac{q(\boldsymbol{z})}{p(\boldsymbol{z})}\right] = -\mathrm{KL}[p(\boldsymbol{z}) \parallel q(\boldsymbol{z})].

\end{aligned}

\]

因此这一项就是要凑的那个 KL 散度。由于得不到 \(p(\boldsymbol{z})\) 的解析式，KL 散度这一项无法被直接优化，它放在这里只是为了证明变分近似的合理性，详见下文。

综上所述，互信息 \(I(Z, X)\) 可以拆成两部分：

\[\begin{aligned}

I(Z, X; \boldsymbol{\theta})

& = \mathbb{E}_{\boldsymbol{x} \sim p(\boldsymbol{x})}[\mathrm{KL}[p(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\theta}) \parallel q(\boldsymbol{z})]] - \mathrm{KL}[p(\boldsymbol{z}) \parallel q(\boldsymbol{z})] \\

& = R(Z, X; \boldsymbol{\theta}) - \mathrm{KL}[p(\boldsymbol{z}) \parallel q(\boldsymbol{z})].

\end{aligned}

\]

由 KL 散度的非负性可知，rate \(R\) 是互信息 \(I(Z, X; \boldsymbol{\theta})\) 的上界：

\[R(Z, X; \boldsymbol{\theta}) = I(Z, X; \boldsymbol{\theta}) + \mathrm{KL}[p(\boldsymbol{z}) \parallel q(\boldsymbol{z})] \geq I(Z, X; \boldsymbol{\theta}),

\]

这正合我们意愿，因为我们想要最小化互信息 \(I(Z, X; \boldsymbol{\theta})\)，所以我们可以通过最小化它的上界 \(R(Z, X; \boldsymbol{\theta})\) 来间接地实现互信息的最小化，实现“曲线救国”。

最大化 I(Z, Y)

使用如下形式的互信息 \(I(Z, X)\)：

\[I(Z, Y; \boldsymbol{\theta}) = \mathbb{E}_{(\boldsymbol{y}, \boldsymbol{z}) \sim p(\boldsymbol{y}, \boldsymbol{z})}\left[\log\frac{p(\boldsymbol{y}|\boldsymbol{z}; \boldsymbol{\theta})}{p(\boldsymbol{y})}\right] \\

\]

标签的分布 \(p(\boldsymbol{y})\) 可能是无法知道的：如果 \(\boldsymbol{y}\) 是类别标签，那么离散型分布 \(p(\boldsymbol{y})\) 是比较容易求的；但如果 \(\boldsymbol{y}\) 是数值，连续型分布 \(p(\boldsymbol{y})\) 是比较难求的。不过难求的 \(p(\boldsymbol{y})\) 并不影响优化过程，因为

\[\mathbb{E}_{(\boldsymbol{y}, \boldsymbol{z}) \sim p(\boldsymbol{y}, \boldsymbol{z})}[-\log p(\boldsymbol{y})] = -\mathbb{E}_{\boldsymbol{y} \sim p(\boldsymbol{y})}[\log p(\boldsymbol{y})] \overset{\text{def}}{=} \mathrm{H}(Y),

\]

其中 \(\mathrm{H}(Y)\) 表示随机变量 \(Y\) 的信息熵 (entropy)。由于标签 \(Y\) 来自于数据集，不属于优化变量，因此 \(\mathrm{H}(Y)\) 是一个定值，不影响优化过程。

接下来要解决的是 \(p(\boldsymbol{y}|\boldsymbol{z}; \boldsymbol{\theta})\) 难求的问题。这里需要与前一节 \(p(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\theta})\) 的情况相区分，\(X\) 是数据集中的数据，\(Z\) 是可优化的特征，因此对于 \(X \mapsto Z\) 这个过程，我们可以任意指定 \(p(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\theta})\) 的形式，\(p(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\theta})\) 不是难求的。而 \(Y\) 是数据集中的数据，对于 \(Z \mapsto Y\) 这个过程，\(p(\boldsymbol{y}|\boldsymbol{z}; \boldsymbol{\theta})\) 的形式是客观上确定的，我们不能随意指定，\(p(\boldsymbol{y}|\boldsymbol{z})\) 是难求的。

可以用一个形式已知的分布 \(q(\boldsymbol{y}|\boldsymbol{z}; \boldsymbol{\phi})\) 来近似 \(p(\boldsymbol{y}|\boldsymbol{z}; \boldsymbol{\theta})\)：

\[\begin{aligned}

I(Z, Y; \boldsymbol{\theta})

& = \mathbb{E}_{(\boldsymbol{y}, \boldsymbol{z}) \sim p(\boldsymbol{y}, \boldsymbol{z})}[\log p(\boldsymbol{y}|\boldsymbol{z}; \boldsymbol{\theta})] + \mathrm{H}(Y) \\

& = \mathbb{E}_{(\boldsymbol{y}, \boldsymbol{z}) \sim p(\boldsymbol{y}, \boldsymbol{z})}[\log q(\boldsymbol{y}|\boldsymbol{z}; \boldsymbol{\phi})] + \mathbb{E}_{(\boldsymbol{y}, \boldsymbol{z}) \sim p(\boldsymbol{y}, \boldsymbol{z})}\left[\log \frac{p(\boldsymbol{y}|\boldsymbol{z}; \boldsymbol{\theta})}{q(\boldsymbol{y}|\boldsymbol{z}; \boldsymbol{\phi})}\right] + \mathrm{H}(Y) \\

& = \mathbb{E}_{(\boldsymbol{y}, \boldsymbol{z}) \sim p(\boldsymbol{y}, \boldsymbol{z})}[\log q(\boldsymbol{y}|\boldsymbol{z}; \boldsymbol{\phi})] + \iint p(\boldsymbol{z})p(\boldsymbol{y}|\boldsymbol{z}; \boldsymbol{\theta})\log\frac{p(\boldsymbol{y}|\boldsymbol{z}; \boldsymbol{\theta})}{q(\boldsymbol{y}|\boldsymbol{z}; \boldsymbol{\phi})} \mathrm{d}\boldsymbol{y}\mathrm{d}\boldsymbol{z} + \mathrm{H}(Y) \\

& = \mathbb{E}_{(\boldsymbol{y}, \boldsymbol{z}) \sim p(\boldsymbol{y}, \boldsymbol{z})}[\log q(\boldsymbol{y}|\boldsymbol{z}; \boldsymbol{\phi})] + \mathbb{E}_{\boldsymbol{z} \sim p(\boldsymbol{z})}[\mathrm{KL}[p(\boldsymbol{y}|\boldsymbol{z}; \boldsymbol{\theta}) \parallel q(\boldsymbol{y}|\boldsymbol{z}; \boldsymbol{\phi})]] + \mathrm{H}(Y) \\

& \geq \mathbb{E}_{(\boldsymbol{y}, \boldsymbol{z}) \sim p(\boldsymbol{y}, \boldsymbol{z})}[\log q(\boldsymbol{y}|\boldsymbol{z}; \boldsymbol{\phi})] + \mathrm{H}(Y) \overset{\text{def}}{=}I_{\text{BA}}.

\end{aligned}

\]

利用 KL 散度的非负性，可以得到互信息 \(I(Z, Y; \boldsymbol{\theta})\) 的一个下界 \(I_{\text{BA}}\)，它被称为互信息的 Barber & Agakov 下界。

由 \(p(\boldsymbol{y}, \boldsymbol{z}) = \int_x p(\boldsymbol{x}, \boldsymbol{y}, \boldsymbol{z}) \mathrm{d}\boldsymbol{x}\) 可得

\[\begin{aligned}

\mathbb{E}_{(\boldsymbol{y}, \boldsymbol{z}) \sim p(\boldsymbol{y}, \boldsymbol{z})}[\log q(\boldsymbol{y}|\boldsymbol{z}; \boldsymbol{\phi})]

& = \iint \left(\int_x p(\boldsymbol{x}, \boldsymbol{y}, \boldsymbol{z}) \mathrm{d}\boldsymbol{x}\right) \log q(\boldsymbol{y}|\boldsymbol{z}; \boldsymbol{\phi})\mathrm{d}\boldsymbol{y}\mathrm{d}\boldsymbol{z} \\

& = \iiint p(\boldsymbol{x}, \boldsymbol{y})p(\boldsymbol{z}|\boldsymbol{x}, \boldsymbol{y}; \boldsymbol{\theta})\log q(\boldsymbol{y}|\boldsymbol{z}; \boldsymbol{\phi}) \mathrm{d}\boldsymbol{x}\mathrm{d}\boldsymbol{y}\mathrm{d}\boldsymbol{z} \\

& = \iiint p(\boldsymbol{x}, \boldsymbol{y})p(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\theta})\log q(\boldsymbol{y}|\boldsymbol{z}; \boldsymbol{\phi}) \mathrm{d}\boldsymbol{x}\mathrm{d}\boldsymbol{y}\mathrm{d}\boldsymbol{z} \\

& = \mathbb{E}_{(\boldsymbol{x}, \boldsymbol{y}) \sim p(\boldsymbol{x}, \boldsymbol{y})}[\mathbb{E}_{\boldsymbol{z} \sim p(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\theta})}[\log q(\boldsymbol{y}|\boldsymbol{z}; \boldsymbol{\phi})]] \\

& \approx \frac{1}{NM}\sum_{i=1}^N\sum_{j=1}^M \log q(\boldsymbol{y}_i|\boldsymbol{z}_j; \boldsymbol{\theta}), \quad (x_i, \boldsymbol{y}_i) \sim p(\boldsymbol{x}, \boldsymbol{y}), \boldsymbol{z}_j \sim p(\boldsymbol{z}|x_i; \boldsymbol{\theta}).

\end{aligned}

\]

若 \(Y\) 是连续型数据（回归问题），则选择高斯分布模型作为近似分布 \(q(\boldsymbol{y}|\boldsymbol{z}; \boldsymbol{\phi})\)，最大化 \(\log q(\boldsymbol{y}|\boldsymbol{z}; \boldsymbol{\phi})\) 对应最小化 MSE 损失。若 \(Y\) 是离散型数据（分类问题），则选择伯努利分布（二分类模型）或类别分布（多分类模型）模型作为近似分布 \(q(\boldsymbol{y}|\boldsymbol{z}; \boldsymbol{\phi})\)，最大化 \(\log q(\boldsymbol{y}|\boldsymbol{z}; \boldsymbol{\phi})\) 对应最小化交叉熵损失。详细的推导过程可参考从极大似然估计到变分自编码器 - VAE 公式推导中“重构损失”这一节。

\(N\) 的意思是从数据集中采样 \(N\) 个训练数据 \((\boldsymbol{x}_1, \boldsymbol{y}_1), \ldots, (\boldsymbol{x}_N, \boldsymbol{y}_N)\)。\(M\) 的意思是对于每个样本 \(\boldsymbol{x}_i\)，从分布 \(p(\boldsymbol{z}|\boldsymbol{x}_i; \boldsymbol{\theta})\) 中采样 \(M\) 个特征 \(\boldsymbol{z}\) 来计算 \(M\) 次 MSE/交叉熵损失。

一些理解

总的来说，最大化 \(I(Z, Y)\) 对应最小化交叉熵损失，最小化 \(I(Z, X)\) 对应最小化 KL 散度正则项（即 rate \(R\)）。

变分信息瓶颈与普通判别模型的区别：

1. 将普通判别模型中的确定性编码器 (deterministic encoder)改成了概率编码器 (probabilistic encoder)，给定 \(\boldsymbol{x}\)，普通判别模型会给出唯一的 \(\boldsymbol{z}\)，而 VIB 的 \(\boldsymbol{z}\) 是从某个分布中采样得到的，是一个随机变量。
2. 加入了一个 KL 散度正则项（即 rate \(R\)），希望特征的后验分布 \(p(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\theta})\) 尽量接近标准高斯分布。

从这两点改进来看，变分信息瓶颈与 VAE 非常相似。

为什么最小化 KL 散度能作为正则项？为什么鼓励接近标准高斯分布是一种正则化效果？如果 KL 正则项为 0，则 \(p(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\theta})\) 完全就是标准高斯分布，不包含任何关于样本 \(\boldsymbol{x}\) 的信息，即完全遗忘了 \(\boldsymbol{x}\) 的信息。当然了，这样的特征是不具备任何判别能力的，所以需要通过调节权重系数 \(\beta\) 以在遗忘和预测能力之间取得平衡。

此外，注意到

\[R(Z, X; \boldsymbol{\theta}) = I(Z, X; \boldsymbol{\theta}) + \mathrm{KL}[p(\boldsymbol{z}) \parallel N(\boldsymbol{0}, \boldsymbol{I})],

\]

因此在最小化正则项 \(R(Z, X; \boldsymbol{\theta})\) 时，不仅是在最小化互信息 \(I(Z, X; \boldsymbol{\theta})\)，而且在最小化 \(\mathrm{KL}[p(\boldsymbol{z}) \parallel N(\boldsymbol{0}, \boldsymbol{I})]\)，使得特征 \(Z\) 的分布 \(p(\boldsymbol{z})\) 逐渐趋近于标准高斯分布。标准高斯分布有很多优良的性质，例如，它的各个维度是相互独立的，这就是在鼓励特征 \(Z\) 的各维度解耦。

参考资料

论文原文：Deep Variational Information Bottleneck

• OpenReview (ICLR 2017)
• arXiv

从变分编码、信息瓶颈到正态分布：论遗忘的重要性 - 科学空间

变分信息瓶颈(Variational Information Bottleneck) - Sphinx Garden

迁移学习：互信息的变分上下界 - orion-orion - 博客园; 迁移学习：互信息的变分上下界 - 猎户座的文章 - 知乎