人工智能开发实战MNIST数据集及神经网络完全解析
天涯幺妹 2024-10-04 15:01:02 阅读 81
内容提要
MNIST数据集简介神经元常用函数深度神经网络卷积神经网络介绍循环神经网络
一、MNIST数据集简介
数据集(Dataset)是一类数据的集合。传统的数据集通常表现为表格或者文档形式,每个数值被称为数据资料。
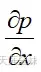
MNIST数据集是一个含有手写数字的大型数据集,包含0~9共10个数字,通常用于训练图像处理系统。
MNIST数据集包含60000个训练图像和10000个测试图像。
MNIST数据集共有4个文件,分别是训练集数据、训练集标签以及测试集数据、测试集标签。MNIST数据集的图像以字节的形式进行存储,每幅图像都为单通道图像,由28×28个像素点构成。
MNIST数据集的测试集样本图像如图所示:
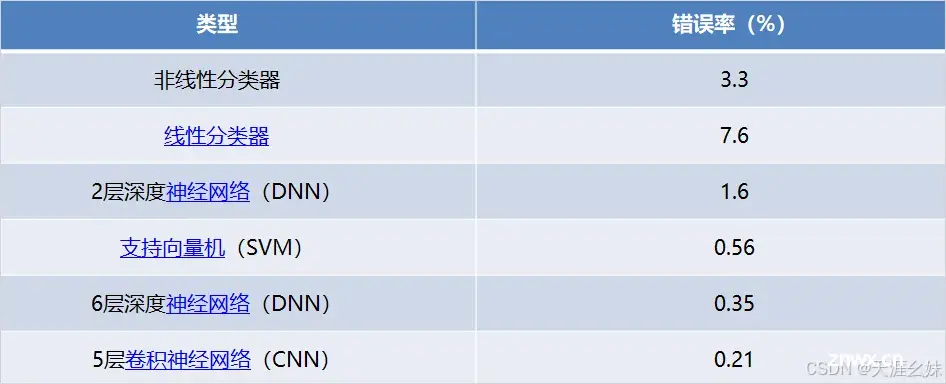
不同分类器使用MNIST数据集的错误率如表所示:

二、神经元常用函数
2.1 激活函数
1、sigmoid()函数
在之前的一段时间内,sigmoid()函数是非常常用的,因为它对神经元的激活有很好的解释,且它本身为单调连续,非常适合作为输出层。
缺陷:
第一,当输入稍微远离了坐标原点,函数的梯度就变得很小了,几乎为0,这会导致在反向传播过程中,梯度很小的时候接近0,神经网络无法更新参数,这个问题称为梯度饱和,也可以称为梯度弥散。
第二,sigmoid()函数的输出不是零中心的,这会影响梯度下降的运作。
2、tanh()函数
tanh()函数的数学公式为
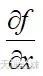
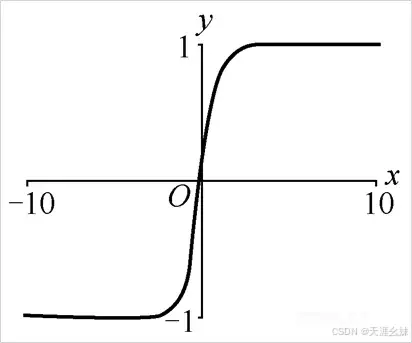
,tanh()函数图像如图所示。
tanh()函数的定义域是实数域 ,值域是(-1,1)。其输入如果是很大的负数,其值就会无限接近于-1。
输入如果是很大的正数,其值就会无限接近于1。
和sigmoid()函数一样,tanh()也存在梯度饱和问题,但是tanh()的输出是零中心的,所以实际使用更多一些。
3、ReLU函数
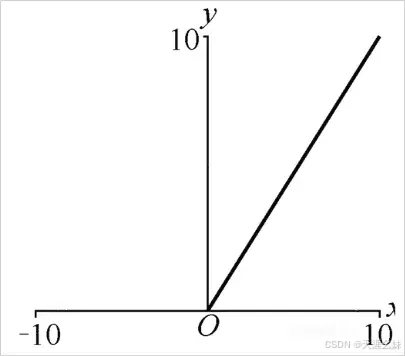
ReLU函数的数学公式为

,ReLU函数图像如图所示。
ReLU函数的定义域是实数 ,值域是[0, +∞] 。这个激活函数可以理解为一个关于0的阈值。
2.2 池化函数
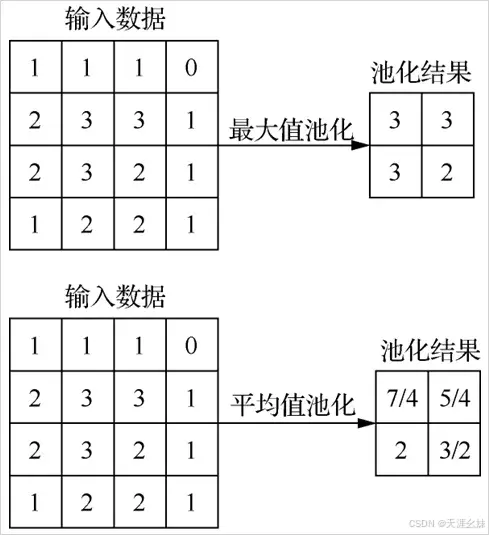
池化是用一个矩阵窗口在张量上进行扫描,通过取最大值或者平均值等方式来减少参数数量的方法。最大值池化和平均值池化的过程如图所示。
池化层主要对输入的图像进行降采样(Subsample),池化并不改变深度或维度,只改变大小。池化函数有平均值池化函数和最大值池化函数等。

1、平均值池化函数
TensorFlow函数:tf.nn.avg_pool(value,ksize,strides,padding,name=None),该函数计算的是池化区域的平均值。
value:需要池化的输入,一般池化层接在卷积层后面,这是一个四维的张量,4个维度为[batch,height,width,channels]。
ksize:池化窗口的大小,是一个四维向量,一般是[1,height,width,1]。
strides:和卷积类似,是窗口在每一个维度上滑动的步长,一般是[1,stride,stride,1]。
padding:和卷积类似,可以取“VALID”或“SAME”。
name:该池化的名称。
2、最大值池化函数
TensorFlow函数:tf.nn.max_pool(value,ksize,strides,padding,name=None),该函数计算的是池化区域的最大值。
在池化时一般选择最大值池化。
2.3 损失函数
1、hinge损失函数
hinge损失函数源自支持向量机,在支持向量机中,最终的目的是最大化分类间隔,减少错误分类的样本数目。
损失函数公式为
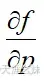
,其中,
, 是一个超参数,设置为1.0时,在绝大多数情况下都是安全的。
2、square损失函数
损失函数公式为
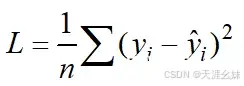
,大多用在线性回归中。
3、log损失函数
在使用似然函数最大化时,其形式是进行连乘,但是为了便于处理,一般会加上log,这样便可以将连乘转换为求和。
由于log函数是单调递增函数,因此不会改变优化结果。log类型的损失函数也是一种常见的损失函数。
4、交叉熵
如何判断输出的结果与期望结果有多接近呢?
交叉熵(Cross Entropy)是常用的方法之一。
交叉熵的公式为
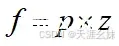
, 是分类问题的真实分布概率, 是分类问题的预测分布概率,也就是说,交叉熵的输入是概率,范围是[0,1]。
交叉熵得到的值越小,真实分布概率和预测分布概率越接近,预测的结果就越真实。
由于网络的输出是任意的,如ReLU函数的值域为 ,所以在进行交叉熵计算之前还需要将输出结果转换为概率分布。
softmax()函数就是一个常用的方法,它的公式为
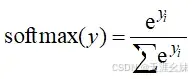
,该函数所有输出值的和为1,输入的负数会变成正数,然后外面嵌套 函数,就可以得到优化结果。
三、深度神经网络
深度神经网络(Deep Neural Networks,DNN)可以理解为有很多隐藏层的神经网络。
具有一层隐藏层的神经网络如图所示。
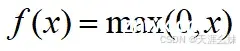
神经网络某个节点的计算公式是

,n为网络的第n层,
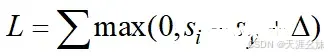
是权重矩阵,

是第一层的偏置矩阵,f()是激活函数,它会作用到每个元素。经过这些激活函数的转换后,由于每个节点不再是线性变换的,所以整个神经网络就成为非线性的了。
反向传播过程:如果有表达式
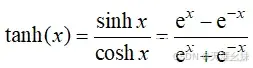
,现在需要求出

,先将这个复合函数的表达式分解为
和

,根据链式求导法则可知

,所以需要分别求出

和
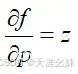
,可以求得
,
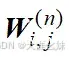
,故得到
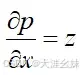
。前向传播与反向传播过程如图所示。
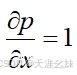
四、卷积神经网络介绍
卷积神经网络(Convolutional Neural Networks,CNN)是一类深度神经网络,最常用于分析视觉图像。
一个简单的卷积神经网络是由各种层按一定顺序排列的。
卷积神经网络主要由卷积层(Convolutional Layers)、池化层(Pooling Layers)、全连接层(Fully Connected Layers,FC Layers)构成。将这些层按一定的顺序排列,就可以搭建一个卷积神经网络。
4.1 LeNet-5模型及其实现
LeNet-5模型是由杨立昆(YannLeCun)教授于1998年在论文Gradient-Based Learning Applied to Document Recognition中提出的,是一种用于手写体字符识别的非常高效的卷积神经网络。
网络实现过程如图。
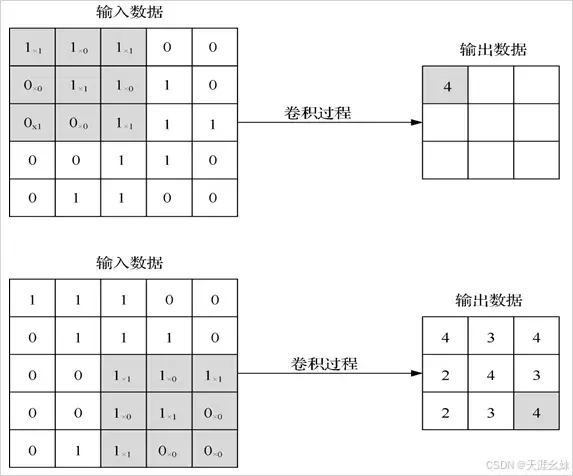
卷积层是一个将卷积运算和加法运算组合在一起的隐藏层,在图像识别里提到的卷积是二维卷积,即离散二维滤波器(也称作卷积核)与二维图像做卷积操作。
简单地讲是二维滤波器滑动到二维图像上的所有位置,并在每个位置上与该像素点及其领域像素点做内积,卷积运算过程如图所示:
1、LeNet-5实现的过程
(1) 输入层
(2)卷积层(第一层)
(3)池化层(第二层)
(4)卷积层(第三层)
(5)池化层(第四层)
(6)全连接层(第五层)
(7)全连接层(第六层)
(8)全连接层,输出层(第七层)
2、欠拟合
欠拟合(Under Fitting)是由于特征维度过少,模型过于简单,使神经网络没办法完全满足数据集的特征提取要求,体现在训练以及预测时表现不佳、成功率低。欠拟合解决方法如下。
(1)将模型复杂化。
(2)增加更多特征,使输入数据的特征更明显。
(3)调整超参数。
(4)减弱正则化约束或者去掉正则化约束。
3、过拟合
过拟合是指模型在训练集上表现很好,但在验证和测试阶段效果比较差,即模型的泛化能力很差。过拟合的解决方法如下。
(1)增加训练数据量。
(2)减少数据特征,去掉数据中非共性的特征。
(3)调整超参数。
(4)使用正则化约束或者增强正则化约束。
(5)降低模型的复杂度。
(6)使用Dropout。
(7)Early Stopping,即提前结束训练。
4、卷积神经网络的TensorFlow实现
通过TensorFlow框架实现一个类似于LeNet-5的神经网络,来解决MNIST数据集上的数字识别问题。
本网络与原LeNet-5的区别是:卷积核的个数不同;激活函数不同,
此处用的是ReLU,输出层选择softmax()函数,二者的整体过程是一致的。
案例1:在TensorFlow目录下新建文件,命名为LeNet-5.py,利用TensorFlow解决类似于LeNet-5在MNIST数据集上进行数字识别的问题,在PyCharm中编写以下代码。
<code># -×- coding: utf-8 -×-
# 载入MINIST数据需要的库
from tensorflow.examples.tutorials.mnist import input_data
# 保存模型需要的库
from tensorflow.python.framework.graph_util import convert_variables_to_constants
from tensorflow.python.framework import graph_util
# 导入其他库
import tensorflow as tf
import time
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'
# 获取MINIST数据
mnist = input_data.read_data_sets("./MNIST_data", one_hot=True)
# 占位符
# x是特征值,也就是像素
# 使用一个28×28=784列的数据来表示一个图像的构成
# 每一个点都是这个图像的一个特征
# 因为每一个点都会对图像的外观和表达的含义有影响,只是影响的大小不同而已
x = tf.placeholder("float", shape=[None, 784], name="Mul") # 输入28×28=784code>
# y_是真实数据[0,0,0,0,1,0,0,0,0],为4
y_ = tf.placeholder("float", shape=[None, 10], name="y_") # 输出code>
# 变量 784×10的矩阵
# W表示每一个特征值(像素点)影响结果的权重
# 这个值很重要,因为深度学习的过程就是发现特征
# 经过一系列训练,得出每一个特征值对结果影响的权重
W = tf.Variable(tf.zeros([784, 10]), name='x')code>
b = tf.Variable(tf.zeros([10]), 'y_')
# 权重
def weight_variable(shape):
# 生成的值服从具有指定平均值和标准偏差的正态分布
# 如果生成的值大于平均值的两个标准偏差的值,则丢弃重新选择
initial = tf.truncated_normal(shape, stddev=0.1) # 标准差为0.1
return tf.Variable(initial)
# 偏差
def bias_variable(shape):
initial = tf.constant(0.1, shape=shape)
return tf.Variable(initial)
# 卷积
def conv2d(x, W):
# 参数x指需要做卷积的输入图像,要求它是一个Tensor
# 具有[batch, in_height, in_width, in_channels]这样的shape
# 具体含义是[训练时一个batch的图像数量, 图像高度, 图像宽度, 图像通道数]
# 注意这是一个4维的Tensor,batch和in_channels在卷积层中通常设为1
# 参数W相当于CNN中的卷积核,要求它是一个Tensor
# 具有[filter_height, filter_width, in_channels, out_channels]这样的shape
# 具体含义是[卷积核的高度,卷积核的宽度,图像通道数,卷积核个数]
# 注意,第三维in_channels就是参数x的第四维
return tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding='VALID')code>
# 参数strides:卷积时在图像每一维的步长,这是一个一维的向量,长度为4
# 参数padding:string类型的量,只能是“VALID”,不补零
# 最大池化
def max_pool_2x2(x):
# x:input
# ksize:filter,滤波器大小为2×2
# strides:步长,2×2,表示filter窗口每次水平移动两格,每次垂直移动两格
# padding:填充方式,补零
return tf.nn.max_pool(x, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')code>
# 第一层卷积
# 权重+偏置+激活+池化
# patch为5×5;in_size为1,即图像的厚度,如果是彩色的,则为3;32个卷积核(滤波器)
W_conv1 = weight_variable([5, 5, 1, 32])
b_conv1 = bias_variable([32])
# 对数据进行重新排列,形成图像
x_image = tf.reshape(x, [-1, 28, 28, 1])
# print("x",x)
# print("x_image",x_image)
# ReLU操作,输出大小为28×28×32
h_conv1 = tf.nn.relu(conv2d(x_image, W_conv1) + b_conv1)
# Pooling操作,输出大小为14×14×32
h_pool1 = max_pool_2x2(h_conv1)
# 第二层卷积
# 权重+偏置+激活+池化
# patch为5×5;in_size为32,即图像的厚度;out_size是64,即输出的大小
W_conv2 = weight_variable([5, 5, 32, 64])
b_conv2 = bias_variable([64])
# ReLU操作,输出大小为14×14×64
h_conv2 = tf.nn.relu(conv2d(h_pool1, W_conv2) + b_conv2)
# Pooling操作,输出大小为7×7×64
h_pool2 = max_pool_2x2(h_conv2)
# 全连接一
W_fc1 = weight_variable([7 × 7 × 64, 1024])
b_fc1 = bias_variable([1024])
# 全连接二
W_fc2 = weight_variable([1024, 10])
b_fc2 = bias_variable([10])
# 输入数据变换
# 变换为m×n,列n为7×7×64
h_pool2_flat = tf.reshape(h_pool2, [-1, 7 × 7 × 64])
# 进行全连接操作
# tf.nn.relu()函数可将大于0的数保持不变,将小于0的数置为0
h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1)
# Dropout可防止过拟合,它一般用在全连接层,训练用,测试不用
# Dropout就是在不同的训练过程中随机扔掉一部分神经元
# Dropout可以让某个神经元的激活值以一定的概率p停止工作
# 参数keep_prob:设置神经元被选中的概率,在初始化时keep_prob是一个占位符
# TensorFlow在运行时设置keep_prob具体的值,如keep_prob: 0.5
keep_prob = tf.placeholder("float", name='rob')code>
h_fc1_drop = tf.nn.dropout(h_fc1, keep_prob)
# 用于训练的softmax()函数将所有数据归一化到0~1之间,大的数据特征更明显
y_conv = tf.nn.softmax(tf.matmul(h_fc1_drop, W_fc2) + b_fc2, name='res')code>
# 训练完成后,进行测试用的softmax()函数
y_conv2 = tf.nn.softmax(tf.matmul(h_fc1, W_fc2) + b_fc2, name="final_result")code>
# 交叉熵的计算,返回包含了损失值/误差的Tensor
# 熵是衡量事物混乱程度的一个值
cross_entropy = -tf.reduce_sum(y_ × tf.log(y_conv))
# 优化器,负责最小化交叉熵
train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy)
# tf.argmax():取出该数组最大值的下角标
correct_prediction = tf.equal(tf.argmax(y_conv, 1), tf.argmax(y_, 1))
# 计算准确率
accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))
# 创建会话
with tf.Session() as sess:
time_begin = time.time()
# 初始化所有变量
sess.run(tf.global_variables_initializer())
# print(sess.run(W_conv1))
# 保存输入/输出,可以在之后用
tf.add_to_collection('res', y_conv)
tf.add_to_collection('output', y_conv2)
tf.add_to_collection('x', x)
### 训练开始 ###
for i in range(10000):
# 取出MNIST数据集中的50个数据
batch = mnist.train.next_batch(50)
# run()可以看作输入相关值到函数中的占位符,然后计算出结果
# 这里将batch[0]给x,将batch[1]给y_
# 执行训练过程并传入真实数据
train_step.run(feed_dict={x: batch[0], y_: batch[1], keep_prob: 0.5})
if i % 100 == 0:
train_accuracy = accuracy.eval(feed_dict={x: batch[0], y_: batch[1], keep_prob: 1.0})
print("step %d, training accuracy %g" % (i, train_accuracy))
time_elapsed = time.time() - time_begin
print("训练所用时间:%d秒" % time_elapsed)
# 用saver 保存模型
saver = tf.train.Saver()
saver.save(sess, "model_data/model")
执行该程序,如果计算机安装的是CPU版本的TensorFlow,建议将训练步数调少,否则会训练非常久。
训练完成后的准确率如图所示。
生成的模型在TensorFlow目录下的model_data目录中,模型文件如图所示。

提示:
LeNet-5模型的结构比较清晰,即输入层→卷积层(池化层)→全连接层→输出层,但是有些网络中是没有池化层的。
4.2 AlexNet介绍
AlexNet模型是2012年大规模视觉识别挑战赛中的冠军模型,AlexNet将LeNet的思想发扬光大,把CNN的基本原理应用到了更深、更宽的网络结构中。
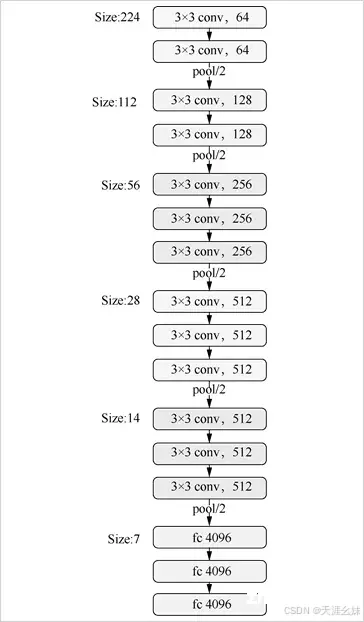
另外,AlexNet模型首次在CNN中采取了ReLU激活函数、Dropout防止过拟合、GPU加速训练等技术,16层的VGGNet网络结构如图所示。
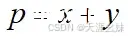
4.3 Inception模型及其实现
1、Inception模型介绍
Inception模型是通过串联+并联的方式将卷积层连接起来的。
Inception模型是对输入图像并行地执行多个卷积运算或池化操作,并将所有输出结果拼接为一个非常深的特征图,且不同大小卷积核的卷积运算可以得到图像中的不同信息,处理获取到的图像中的不同信息可以得到更好的图像特征。
Inception模型的主要成员包括:Inception v1、Inception v2、Inception v3、Inception v4和Inception-ResNet。
这里给出了Inception模块的一个单元结构示意图。
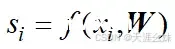
由于一个Inception模块要进行多次运算,所以需要耗费大量的计算资源。为了实现降维,降低运算成本,在3×3、5×5的卷积运算前,在最大值池化的运算后,加入1×1的卷积核。
如下为降维的Inception模块的一个单元结构示意图。
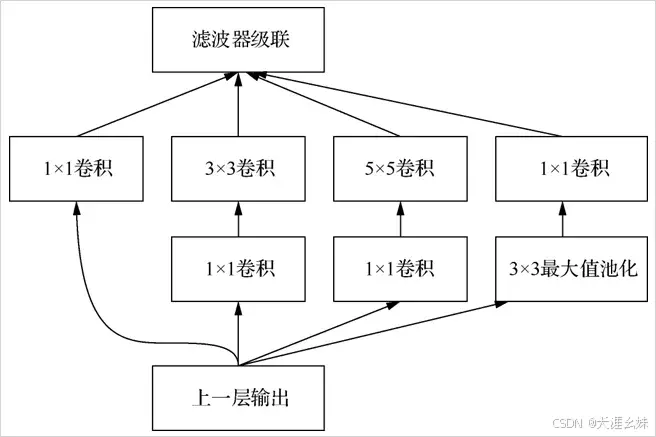
2、GoogLeNet实现的过程
这里以Inception模块构建的GoogLeNet(Inception v1)为例,描述GoogLeNet的实现过程。
(1)输入层:原始输入图像大小为224×224×3,为三通道RGB图像。
(2)卷积层:接收224×224×3的矩阵数据,与64个大小为7×7的卷积核(步长为2,padding为“SAME”)做运算,输出为112×112×64,经过3×3的最大值池化(步长为2),输出矩阵为56×56×64。
(3)卷积层:接收56×56×64的矩阵数据,与192个大小为3×3的卷积核(步长为1,padding为“SAME”)做运算,输出为56×56×192,经过3×3的最大值池化(步长为2),输出矩阵为28×28×192。
(4)Inception 3a层:接收28×28×192的矩阵数据,共4个分支,采用不同尺度的卷积核运算,4个分支步长都为1。
(5)之后的层:以后的层数都以此类推,GoogLeNet模型有9个堆叠的Inception模块,共有22层(如果包括池化层,则是27层)。
五、循环神经网络RNN
循环神经网络(Recurrent Neural Network, RNN)是一类以序列(sequence)数据为输入,在序列的演进方向进行递归(recursion)且所有节点(循环单元)按链式连接的递归神经网络(recursive neural network)。
时间序列数据是序列数据中最常见的一种。时间序列数据(Time Series Data)是在不同时间上收集到的数据,用于描述现象随时间变化的情况。这类数据反映了某一事物、现象等随时间的变化状态或程度。
在全连接的神经网络以及卷积神经网络中有输入层、隐藏层、输出层,层与层之间通过学习到的权重进行连接,在同一层中,节点与节点之间是不连接的。
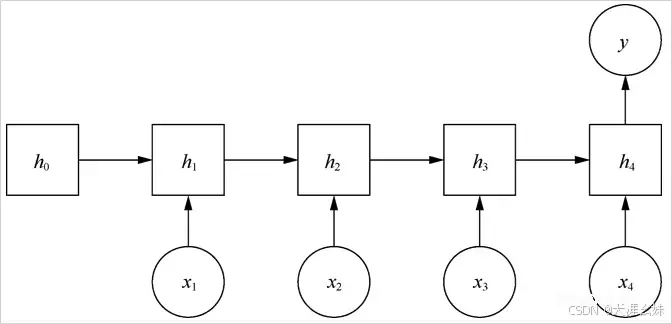
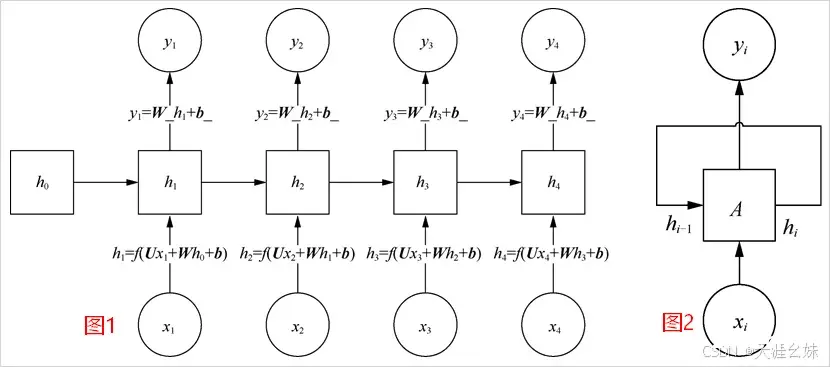
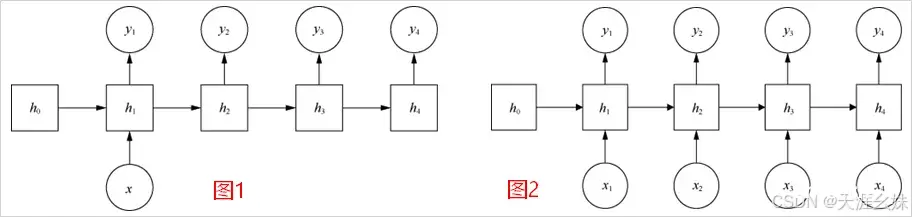
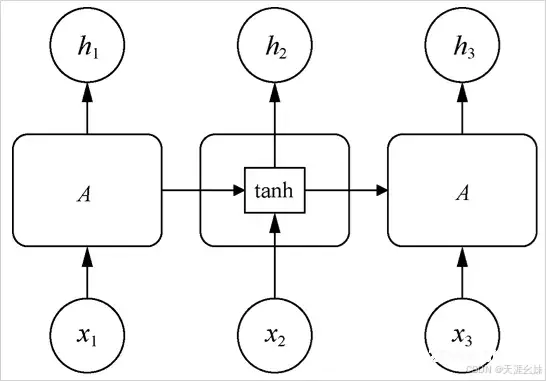
1、RNN基本结构
从RNN基本结构可以看出,RNN的输入和输出是等长的。图1中有4个序列,但实际上序列数是不定的,假设有不定个序列,可以组成RNN不展开表达样式,如图2所示,其中A为某特殊序列。

2、RNN结构分析
RNN常用的结构有3种,分别是Vector-to-Sequence结构、Sequence-to-Vector结构、Encoder-Decoder结构。
(1)Vector-to-Sequence结构
假设一个问题的输入是单独的值,输出是一个序列,则可以建立Vector-to-Sequence结构模型,将输入放到某一个序列进行计算(如图1所示),也可以将输入放到全部序列中进行计算(如图2所示)。
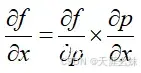
(2)Sequence-to-Vector结构
假设一个问题的输入是一个序列,输出是一个单独的值,一般会在最后一个序列上进行输出变换,可以建立Sequence-to-Vector结构,如图5所示。
(3)Encoder-Decoder结构
有时也会将Encoder-Decoder结构称为Sequence-to-Sequence结构,该结构的具体过程就是编码及解码。
首先将输入的数据编码成一个上下文向量c,这个过程称为Encoder,得到c后,用另一个RNN网络进行解码,这个过程称为Decoder。c作为新的RNN的h0时,结构如图5-21所示;c作为新的输入时,结构如图所示。
3、长短期记忆网络结构
RNN可以做到在时间序列上记忆,但是对于时间序列上较远的点,记起来比较困难,因为两个节点距离较远时,会涉及多次的雅可比矩阵相乘,导致梯度消失或者梯度膨胀,长短期记忆网络(Long Short-Term Memory,LSTM)结构可以很好地解决这个问题。
在标准的RNN结构中,会重复一些简单的结构,如tanh层,简化后的RNN标准模型如图所示。

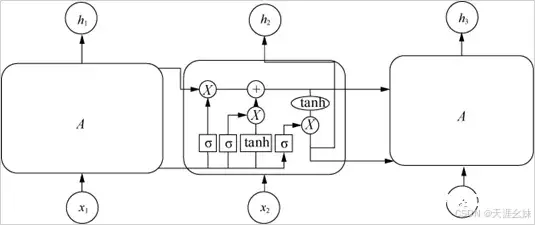
虽然LSTM与RNN的大体结构相同,但是LSTM在重复模块中拥有一个不同的结构,LSTM结构如图。

LSTM靠门结构有选择性地处理信息,每一个门包含一个sigmoid神经网络层和一个pointwise乘法操作。
LSTM共拥有3个门,分别是遗忘门、输入门和输出门,用来保护和控制状态。遗忘门将状态中的信息选择性地遗忘,输入门将新的信息选择性地记录下来,输出门确定输出什么值。
案例2:在TensorFlow目录下新建文件,命名为LSTM.py,利用TensorFlow解决类似于LSTM在MNIST数据集上进行数字识别的问题,在PyCharm中编写以下代码。
<code>import tensorflow as tf
from tensorflow.contrib import rnn
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'
# 导入MNIST数据集
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("./MNIST_data/", one_hot=True)
# 设置全局变量
learning_rate = 0.001
training_steps = 10000
batch_size = 128
display_step = 200
num_input = 28 # 输入向量的维度
timesteps = 28 # 循环层长度
num_hidden = 128 # 隐藏层的特征数
num_classes = 10 # 0~9
# tf Graph 输入
X = tf.placeholder("float", [None, timesteps, num_input])
Y = tf.placeholder("float", [None, num_classes])
# 定义权重和偏置
weights = {
'out': tf.Variable(tf.random_normal([num_hidden, num_classes]))
}
biases = {
'out': tf.Variable(tf.random_normal([num_classes]))
}
def RNN(x, weights, biases):
x = tf.unstack(x, timesteps, 1)
# 初始的biases=1,不希望遗忘任何信息
lstm_cell = rnn.BasicLSTMCell(num_hidden, forget_bias=1.0)
outputs, states = rnn.static_rnn(lstm_cell, x, dtype=tf.float32)
# 选择最后一个output与输出的全连接weights相乘,再加上biases
return tf.matmul(outputs[-1], weights['out']) + biases['out']
logits = RNN(X, weights, biases)
prediction = tf.nn.softmax(logits)
# 定义损失和优化
loss_op = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=logits, labels=Y))
optimizer = tf.train.GradientDescentOptimizer(learning_rate=learning_rate)
train_op = optimizer.minimize(loss_op)
correct_pred = tf.equal(tf.argmax(prediction, 1), tf.argmax(Y, 1))
accuracy = tf.reduce_mean(tf.cast(correct_pred, tf.float32))
init = tf.global_variables_initializer()
with tf.Session() as sess:
sess.run(init)
for step in range(1, training_steps+1):
# 随机抽出这一次迭代训练时用的数据
batch_x, batch_y = mnist.train.next_batch(batch_size)
# 对数据进行处理,使得其符合输入
batch_x = batch_x.reshape((batch_size, timesteps, num_input))
# 迭代
sess.run(train_op, feed_dict={X: batch_x, Y: batch_y})
if step % display_step == 0 or step == 1:
# 计算损失
loss, acc = sess.run([loss_op, accuracy], feed_dict={X: batch_x, Y: batch_y})
print("Step " + str(step) + ", Minibatch Loss= " + "{:.4f}".format(loss) + ", Training Accuracy= " + "{:.3f}".format(acc))
print("优化完成!")
# 计算128个测试的准确率
test_len = 128
test_data = mnist.test.images[:test_len].reshape((-1, timesteps, num_input))
test_label = mnist.test.labels[:test_len]
print("测试准确率:", sess.run(accuracy, feed_dict={X: test_data, Y: test_label}))
更多精彩内容请继续关注本站!
声明
本文内容仅代表作者观点,或转载于其他网站,本站不以此文作为商业用途
如有涉及侵权,请联系本站进行删除
转载本站原创文章,请注明来源及作者。