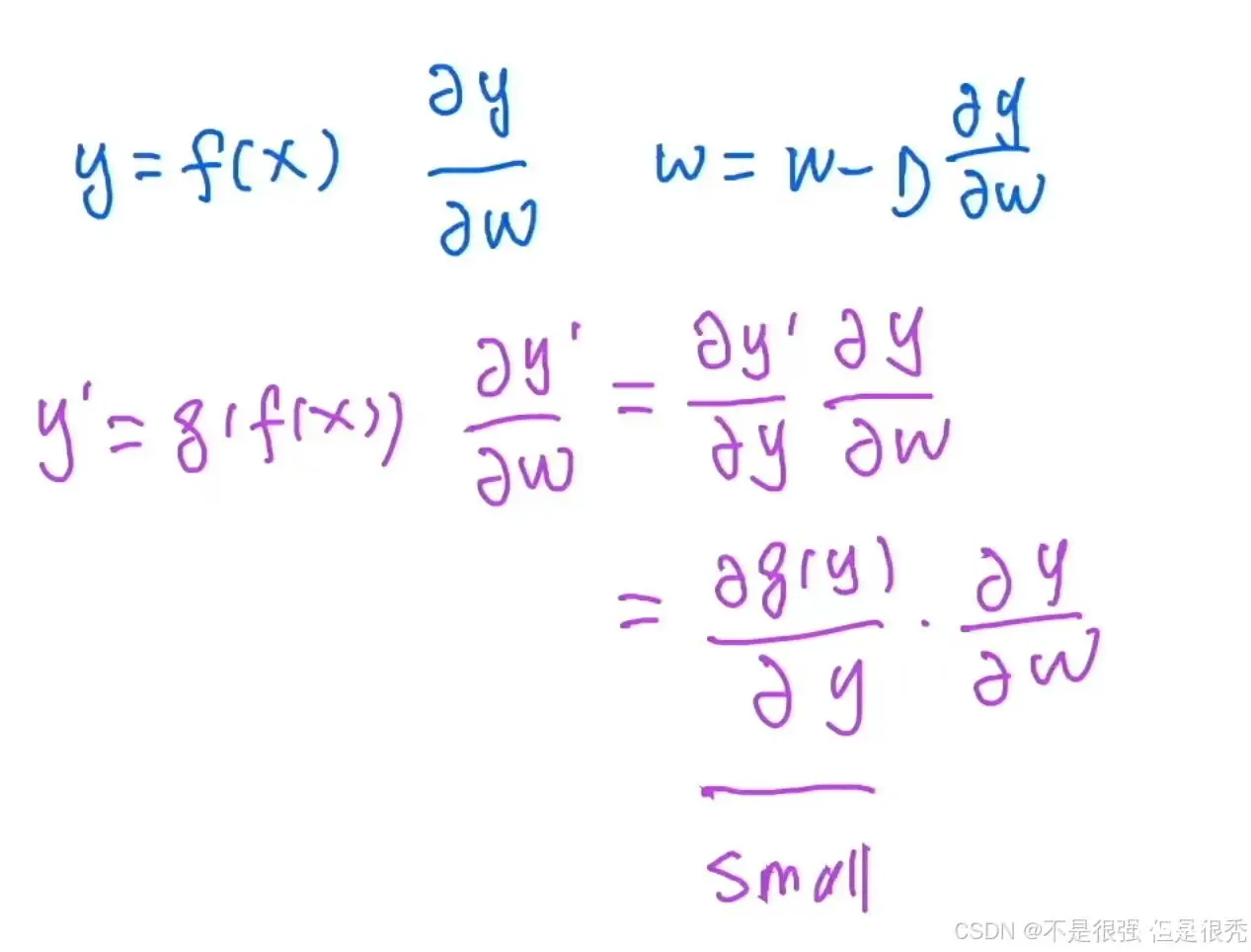目录

残差网络——ResNet

残差块思想

ResNet块细节

ResNet架构

总结

代码实现

残差块

两种 ResNet 块的情况 

ResNet 模型

QA

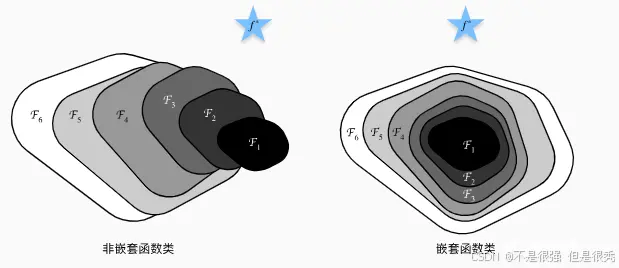
由上图发现，只有当较复杂的函数类包含较小的函数类时，才能确保提高它们的性能。

对于深度神经网络，如果我们能将新添加的层训练成恒等映射（identity function）f(x)=x，新模型和原模型将同样有效。 同时，由于新模型可能得出更优的解来拟合训练数据集，因此添加层似乎更容易降低训练误差。

针对这一问题，何恺明等人提出了残差网络（ResNet） 。它在2015年的 ImageNet 图像识别挑战赛夺魁，并深刻影响了后来的深度神经网络的设计。

残差网络——ResNet

残差网络的核心思想是：每个附加层都应该更容易地包含原始函数作为其元素之一。

于是，残差块（residual blocks）便诞生了，这个设计对如何建立深层神经网络产生了深远的影响。 凭借它，ResNet赢得了2015年ImageNet大规模视觉识别挑战赛。

残差块思想

残差块加入快速通道来得到f(x) = x + g(x) 的结构

如下图所示，假设我们的原始输入为x，而希望学出的理想映射为 f(x)（作为上方激活函数的输入）。

左图虚线框中的部分需要直接拟合出该映射 f(x)，而右图虚线框中的部分则需要拟合出残差映射 f(x)−x。残差映射在现实中往往更容易优化。

开头提到的恒等映射作为我们希望学出的理想映射 f(x)，我们只需将右图虚线框内上方的加权运算（如仿射）的权重和偏置参数设成 0，那么 f(x) 即为恒等映射。 实际中，当理想映射 f(x) 极接近于恒等映射时，残差映射也易于捕捉恒等映射的细微波动。

右图是 ResNet 的基础架构–残差块（residual block）。 在残差块中，输入可通过跨层数据线路更快地向前传播。

相当于ResNet觉得，你就算虚线框里面所有层都没学到东西，下一层还是可以接收到这层的上一层传递来的东西（残差连接）即一个简单的直接传递的小模型。这个想法从函数的角度来说，可以认为更大、更复杂的模型里面包含一个小模型。

ResNet块细节

ResNet 是从 VGG 过来的，所以采用的是 3x3Conv

以下是 ResNet 块的两个不同的实现

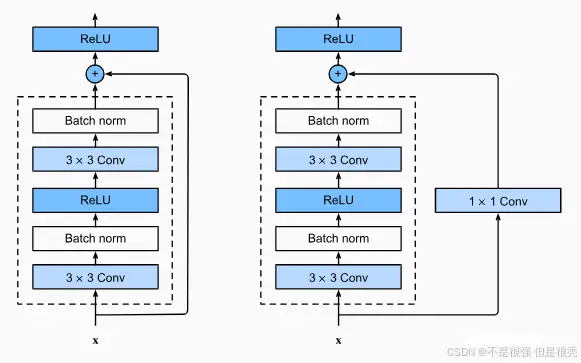
右边存在的意义是：如果虚线的block对通道做了变换，那直接的X加不回去了，所以需要用卷积来对x做一个通道数的变换用于相加 。

ResNet架构

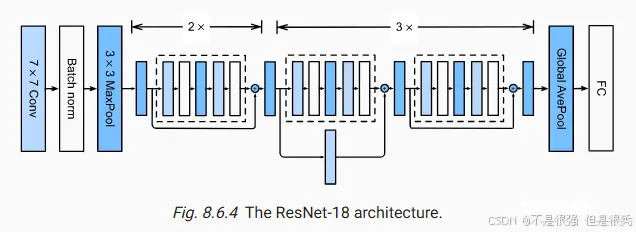
ResNet 最主要的思想就是单拎出来一条路让你可以把输入和输出加起来

抛开这个其他的你可以认为和 VGG 以及GoogLeNet 很像，也是由5个Stage拼成，只是把组合成网络的 Stage 替换成了 ResNet 块

一个高宽减半的 ResNet 块（步幅为2）（那个支线上有Conv的Block，用来把输入的通道数翻一倍）重复多个高宽不变的 ResNet 块 

总结

残差块使得很深的网络更加容易训练

甚至可以训练以前层的网络

残差网络对随后的深层神经网络设计产生了深远的影响，无论是卷积类网络还是全连接类网络 

学习嵌套函数（nested function）是训练神经网络的理想情况。在深层神经网络中，学习另一层作为恒等映射（identity function）较容易（尽管这是一个极端情况）。

残差映射可以更容易地学习同一函数，例如将权重层中的参数近似为零。

利用残差块（residual blocks）可以训练出一个有效的深层神经网络：输入可以通过层间的残余连接更快地向前传播。

代码实现

残差块

<code>import torch

from torch import nn

from torch.nn import functional as F

from d2l import torch as d2l

class Residual(nn.Module): #@save

def __init__(self, input_channels, num_channels,

use_1x1conv=False, strides=1):

super().__init__()

self.conv1 = nn.Conv2d(input_channels, num_channels,

kernel_size=3, padding=1, stride=strides)

self.conv2 = nn.Conv2d(num_channels, num_channels,

kernel_size=3, padding=1)

if use_1x1conv:

self.conv3 = nn.Conv2d(input_channels, num_channels,

kernel_size=1, stride=strides)

else:

self.conv3 = None

self.bn1 = nn.BatchNorm2d(num_channels)

self.bn2 = nn.BatchNorm2d(num_channels)

def forward(self, X):

Y = F.relu(self.bn1(self.conv1(X)))

Y = self.bn2(self.conv2(Y))

if self.conv3:

X = self.conv3(X)

Y += X

return F.relu(Y)

两种 ResNet 块的情况 

输入和输出形状一致

blk = Residual(3,3)

X = torch.rand(4, 3, 6, 6)

Y = blk(X)

Y.shape

# 输出

torch.Size([4, 3, 6, 6])

增加输出通道数的同时，减半输出的高和宽

blk = Residual(3, 6, use_1x1conv=True, strides= 2)

blk(X).shape

# 输出

torch.Size([4, 6, 3, 3])

ResNet 模型

ResNet 的前两层跟之前介绍的 GoogLeNet 中的一样：

在输出通道数为 64、步幅为 2 的 7×7 卷积层后，

接步幅为 2 的 3×3 的最大汇聚层。

不同之处在于 ResNet 每个卷积层后增加了批量规范化层。

b1 = nn.Sequential(nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),

nn.BatchNorm2d(64), nn.ReLU(),

nn.MaxPool2d(kernel_size=3, stride=2, padding=1))

GoogLeNet 在后面接了 4 个由 Inception 块组成的模块。ResNet 则使用 4 个由残差块组成的模块，

每个模块使用若干个同样输出通道数的残差块。

第一个模块的通道数同输入通道数一致。由于之前已经使用了步幅为 2 的最大汇聚层，所以无须减小高和宽。

之后的每个模块在第一个残差块里将上一个模块的通道数翻倍，并将高和宽减半。

def resnet_block(input_channels, num_channels, num_residuals,

first_block=False):

blk = []

for i in range(num_residuals):

if i == 0 and not first_block:

blk.append(Residual(input_channels, num_channels,

use_1x1conv=True, strides=2))

else:

blk.append(Residual(num_channels, num_channels))

return blk

b2 = nn.Sequential(*resnet_block(64, 64, 2, first_block=True))

b3 = nn.Sequential(*resnet_block(64, 128, 2))

b4 = nn.Sequential(*resnet_block(128, 256, 2))

b5 = nn.Sequential(*resnet_block(256, 512, 2))

net = nn.Sequential(b1, b2, b3, b4, b5,

nn.AdaptiveAvgPool2d((1,1)),

nn.Flatten(), nn.Linear(512, 10))

老规矩，不同模块的数据形状变化

X = torch.rand(size=(1, 1, 224, 224))

for layer in net:

X = layer(X)

print(layer.__class__.__name__,'output shape:\t', X.shape)

QA

残差概念体现在哪里？

可以理解成，因为 f(x) 是由 x 和 g(x) 相加得来的，x 又是由上一层网络训练的来的，可以被视为一个小网络的输出。所以整个 ResNet 就是先训练小网络，然后小网络 fit 不到的（小的差距）再由上面的层去补充。这就是残差（残留的差距）的概念。

 为什么 BN 需要定义两个，而 ReLU 不需要？

BN 是两个独立的层，每个层都有自己需要学的不同的参数，而 ReLU 没有什么学习性，所以公用一个层就可以

训练 ACC 是不是在不 overfitting 的情况下，永远大于测试 ACC？

不一定哦，后面会看到当你做了大量的数据噪音的时候，测试精度会高于训练精度，因为你测试的时候不会添加噪声。

为什么 ResNet 可以训练 100 层网络？ 

 假设 g(x) 是在 f(x) 之外新加的一个层，那对于梯度的计算公式根据链式求导法展开，多出来的第一项就是新套的那层的输入和输出求导。假设加的这个层的拟合能力比较强，这一项会很快的变得特别小。一个很小的值乘我们之前那一层的梯度，梯度就会变得比之前小很多。梯度变小之后可以选择增大学习率，但是很有可能增大学习率也没啥用。因为也不能增的太大，f 这一层比 g 更靠近数据，如果增加太大那 g 这一层会变得不稳定。这就是为什么之前模型变深之后会出现梯度消失的问题。

主要原因就是层数叠加，梯度是一直做乘法。回传的时候就会出现底部的梯度特别小。

而 ResNet 是怎么解决这个问题的呢？

因为 ResNet 的网络设计使得它的梯度计算是相加的，哪怕有哪一块比较小也没关系，哪怕当g(x)不存在的时候去拟合，也有 f(x) 的梯度存在。

大数 + 小数没问题，但是 大数*小数问题很大！