非极大值抑制详细原理(NMS含代码及详细注释)
爱笑的男孩。 2024-09-05 13:01:04 阅读 66

作者主页:爱笑的男孩。的博客_CSDN博客-深度学习,YOLO,活动领域博主爱笑的男孩。擅长深度学习,YOLO,活动,等方面的知识,爱笑的男孩。关注算法,python,计算机视觉,图像处理,深度学习,pytorch,神经网络,opencv领域.
https://blog.csdn.net/Code_and516?type=collect
个人介绍:打工人。
分享内容:机器学习、深度学习、python相关内容、日常BUG解决方法及Windows&Linux实践小技巧。
如发现文章有误,麻烦请指出,我会及时去纠正。有其他需要可以私信我或者发我邮箱:zhilong666@foxmail.com
目录
非极大值抑制原理
NMS源码含注释
需要的依赖包
nms算法
绘图
全部代码
效果图
非极大值抑制原理
非极大值抑制(Non-Maximum Suppression,NMS)是一种图像处理中的技术。它通常用于目标检测中,其主要作用是去除检测出来的冗余框,只保留最有可能包含目标物体的框,保留最优的检测结果。
在目标检测中,我们通常使用一个检测器来检测出可能存在的物体,并给出其位置和大小的预测框。然而,同一个物体可能会被多次检测出来,从而产生多个预测框。这时,我们就需要使用NMS来去除掉这些重叠的框,只保留最优的一个。
其基本原理是先在图像中找到所有可能包含目标物体的矩形区域,并按照它们的置信度进行排列。然后从置信度最高的矩形开始,遍历所有的矩形,如果发现当前的矩形与前面任意一个矩形的重叠面积大于一个阈值,则将当前矩形舍去。使得最终保留的预测框数量最少,但同时又能够保证检测的准确性和召回率。具体的实现方法包括以下几个步骤:
对于每个类别,按照预测框的置信度进行排序,将置信度最高的预测框作为基准。
从剩余的预测框中选择一个与基准框的重叠面积最大的框,如果其重叠面积大于一定的阈值,则将其删除。
对于剩余的预测框,重复步骤2,直到所有的重叠面积都小于阈值,或者没有被删除的框剩余为止。
通过这样的方式,NMS可以过滤掉所有与基准框重叠面积大于阈值的冗余框,从而实现检测结果的优化。值得注意的是,NMS的阈值通常需要根据具体的数据集和应用场景进行调整,以兼顾准确性和召回率。
总结来说,非极大值抑制原理是通过较高置信度的目标框作为基准,筛选出与其重叠度较低的目标框,从而去除掉冗余的目标框,提高目标检测的精度和效率。
NMS源码含注释
需要的依赖包
import numpy as np
import matplotlib.pyplot as plt
#安装
#pip install numpy==1.19.5 -i https://pypi.tuna.tsinghua.edu.cn/simple/
#pip install matplotlib==3.2.2 -i https://pypi.tuna.tsinghua.edu.cn/simple/
nms算法
<code>#nms 算法
def py_cpu_nms(dets, thresh):
#边界框的坐标
x1 = dets[:, 0]#所有行第一列
y1 = dets[:, 1]#所有行第二列
x2 = dets[:, 2]#所有行第三列
y2 = dets[:, 3]#所有行第四列
#计算边界框的面积
areas = (y2 - y1 + 1) * (x2 - x1 + 1) #(第四列 - 第二列 + 1) * (第三列 - 第一列 + 1)
#执行度,包围盒的信心分数
scores = dets[:, 4]#所有行第五列
keep = []#保留
#按边界框的置信度得分排序 尾部加上[::-1] 倒序的意思 如果没有[::-1] argsort返回的是从小到大的
index = scores.argsort()[::-1]#对所有行的第五列进行从大到小排序,返回索引值
#迭代边界框
while index.size > 0: # 6 > 0, 3 > 0, 2 > 0
i = index[0] # every time the first is the biggst, and add it directly每次第一个是最大的,直接加进去
keep.append(i)#保存
#计算并集上交点的纵坐标(IOU)
x11 = np.maximum(x1[i], x1[index[1:]]) # calculate the points of overlap计算重叠点
y11 = np.maximum(y1[i], y1[index[1:]]) # index[1:] 从下标为1的数开始,直到结束
x22 = np.minimum(x2[i], x2[index[1:]])
y22 = np.minimum(y2[i], y2[index[1:]])
#计算并集上的相交面积
w = np.maximum(0, x22 - x11 + 1) # the weights of overlap重叠权值、宽度
h = np.maximum(0, y22 - y11 + 1) # the height of overlap重叠高度
overlaps = w * h# 重叠部分、交集
#IoU:intersection-over-union的本质是搜索局部极大值,抑制非极大值元素。即两个边界框的交集部分除以它们的并集。
# 重叠部分 / (面积[i] + 面积[索引[1:]] - 重叠部分)
ious = overlaps / (areas[i] + areas[index[1:]] - overlaps)#重叠部分就是交集,iou = 交集 / 并集
print("ious", ious)
# ious <= 0.7
idx = np.where(ious <= thresh)[0]#判断阈值
print("idx", idx)
index = index[idx + 1] # because index start from 1 因为下标从1开始
return keep #返回保存的值
绘图
#画图函数
def plot_bbox(dets, c='k'):#c = 颜色 默认黑色code>
# 边界框的坐标
x1 = dets[:, 0] # 所有行第一列
y1 = dets[:, 1] # 所有行第二列
x2 = dets[:, 2] # 所有行第三列
y2 = dets[:, 3] # 所有行第四列
plt.plot([x1, x2], [y1, y1], c)#绘图
plt.plot([x1, x1], [y1, y2], c)#绘图
plt.plot([x1, x2], [y2, y2], c)#绘图
plt.plot([x2, x2], [y1, y2], c)#绘图
plt.title("nms")#标题
全部代码
#导入数组包
import numpy as np
import matplotlib.pyplot as plt#画图包
#画图函数
def plot_bbox(dets, c='k'):#c = 颜色 默认黑色code>
# 边界框的坐标
x1 = dets[:, 0] # 所有行第一列
y1 = dets[:, 1] # 所有行第二列
x2 = dets[:, 2] # 所有行第三列
y2 = dets[:, 3] # 所有行第四列
plt.plot([x1, x2], [y1, y1], c)#绘图
plt.plot([x1, x1], [y1, y2], c)#绘图
plt.plot([x1, x2], [y2, y2], c)#绘图
plt.plot([x2, x2], [y1, y2], c)#绘图
plt.title("nms")#标题
#nms 算法
def py_cpu_nms(dets, thresh):
#边界框的坐标
x1 = dets[:, 0]#所有行第一列
y1 = dets[:, 1]#所有行第二列
x2 = dets[:, 2]#所有行第三列
y2 = dets[:, 3]#所有行第四列
#计算边界框的面积
areas = (y2 - y1 + 1) * (x2 - x1 + 1) #(第四列 - 第二列 + 1) * (第三列 - 第一列 + 1)
#执行度,包围盒的信心分数
scores = dets[:, 4]#所有行第五列
keep = []#保留
#按边界框的置信度得分排序 尾部加上[::-1] 倒序的意思 如果没有[::-1] argsort返回的是从小到大的
index = scores.argsort()[::-1]#对所有行的第五列进行从大到小排序,返回索引值
#迭代边界框
while index.size > 0: # 6 > 0, 3 > 0, 2 > 0
i = index[0] # every time the first is the biggst, and add it directly每次第一个是最大的,直接加进去
keep.append(i)#保存
#计算并集上交点的纵坐标(IOU)
x11 = np.maximum(x1[i], x1[index[1:]]) # calculate the points of overlap计算重叠点
y11 = np.maximum(y1[i], y1[index[1:]]) # index[1:] 从下标为1的数开始,直到结束
x22 = np.minimum(x2[i], x2[index[1:]])
y22 = np.minimum(y2[i], y2[index[1:]])
#计算并集上的相交面积
w = np.maximum(0, x22 - x11 + 1) # the weights of overlap重叠权值、宽度
h = np.maximum(0, y22 - y11 + 1) # the height of overlap重叠高度
overlaps = w * h# 重叠部分、交集
#IoU:intersection-over-union的本质是搜索局部极大值,抑制非极大值元素。即两个边界框的交集部分除以它们的并集。
# 重叠部分 / (面积[i] + 面积[索引[1:]] - 重叠部分)
ious = overlaps / (areas[i] + areas[index[1:]] - overlaps)#重叠部分就是交集,iou = 交集 / 并集
print("ious", ious)
# ious <= 0.7
idx = np.where(ious <= thresh)[0]#判断阈值
print("idx", idx)
index = index[idx + 1] # because index start from 1 因为下标从1开始
return keep #返回保存的值
def main():
# 创建数组
boxes = np.array([[100, 100, 210, 210, 0.72],
[250, 250, 420, 420, 0.8],
[220, 220, 320, 330, 0.92],
[100, 100, 210, 210, 0.72],
[230, 240, 325, 330, 0.81],
[220, 230, 315, 340, 0.9]])
show(boxes)
def show(boxes):
plt.figure(1) # 画图窗口、图形
plt.subplot(1, 2, 1) # 子图
plot_bbox(boxes, 'k') # before nms 使用nms(非极大抑制)算法前
plt.subplot(1, 2, 2) # 子图
keep = py_cpu_nms(boxes, thresh=0.7) # nms(非极大抑制)算法
print(keep)
plot_bbox(boxes[keep], 'r') # after nms 使用nms(非极大抑制)算法后
plt.show() # 显示图像
if __name__ == '__main__':
main()
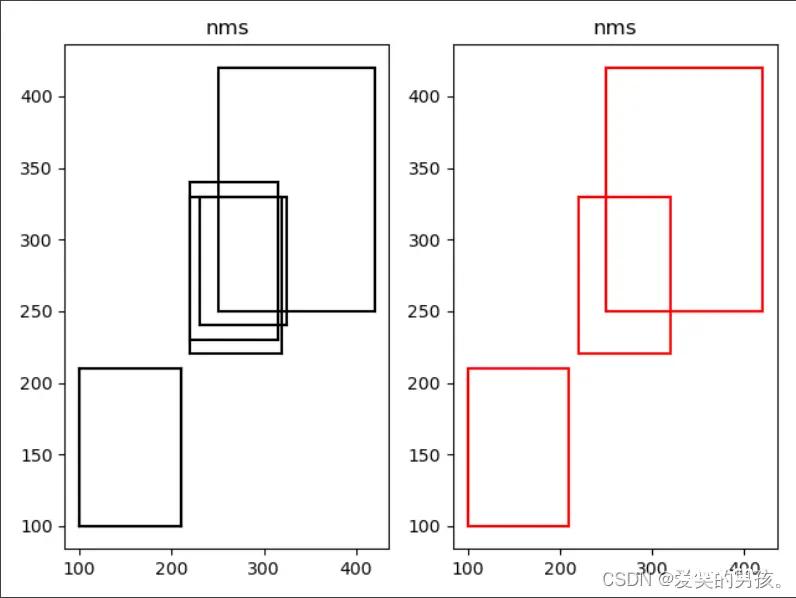
效果图
声明
本文内容仅代表作者观点,或转载于其他网站,本站不以此文作为商业用途
如有涉及侵权,请联系本站进行删除
转载本站原创文章,请注明来源及作者。
