​

大侠幸会，在下全网同名「算法金」 0 基础转 AI 上岸，多个算法赛 Top 「日更万日，让更多人享受智能乐趣」

今日 215/10000

为模型找到最好的超参数是机器学习实践中最困难的部分之一

1. 超参数调优的基本概念

机器学习模型中的参数通常分为两类：模型参数和超参数。模型参数是模型通过训练数据自动学习得来的，而超参数则是在训练过程开始前需要人为设置的参数。理解这两者的区别是进行有效模型调优的基础。

1.1 超参数与模型参数的区别

模型参数是在模型训练过程中通过优化算法学习得来的。例如，线性回归中的权重系数、神经网络中的权重和偏置都是模型参数。这些参数直接影响模型的预测能力，是模型从数据中提取到的信息。

超参数则是由用户在训练模型之前手动设定的参数，不能通过数据自动学习得来。例如，决策树的最大深度、支持向量机的核函数类型、神经网络的学习率和隐藏层数量等都是超参数。超参数的选择直接影响模型的性能和训练效率，因此需要进行仔细调优。

1.2 为什么超参数调优很重要

超参数调优的目的是找到最优的超参数组合，使模型在验证集上的表现最佳。合适的超参数能显著提升模型的性能，而不合适的超参数则可能导致模型的欠拟合或过拟合。

例如，在神经网络中，过高的学习率可能导致模型参数在训练过程中剧烈波动，无法收敛到一个稳定的值；过低的学习率则可能使模型收敛速度过慢，训练时间过长。同样，决策树中过大的树深度可能导致模型过拟合，过小的树深度则可能导致欠拟合。

超参数调优需要结合具体的问题、数据集和模型类型进行选择，通常包括以下几个步骤：

1. 定义要调优的超参数及其可能的取值范围
2. 选择调优策略（如网格搜索、随机搜索等）
3. 使用交叉验证或验证集评估模型性能
4. 根据评估结果选择最优的超参数组合

通过这些步骤，可以有效地提升模型的性能，使其在新数据上的预测更准确。

2. 网格搜索 (Grid Search)

2.1 基本原理

网格搜索是一种系统的超参数调优方法，通过穷举搜索预定义的超参数空间，找到最佳的超参数组合。具体来说，网格搜索会列出所有可能的超参数组合，然后对每个组合进行模型训练和评估，最后选择在验证集上表现最好的组合。

假设我们有两个超参数 𝛼 和 𝛽，每个超参数都有三个可能的取值。网格搜索会尝试所有可能的 (𝛼,𝛽) 组合

通过这种方法，可以保证找到在给定超参数空间内的最优组合。

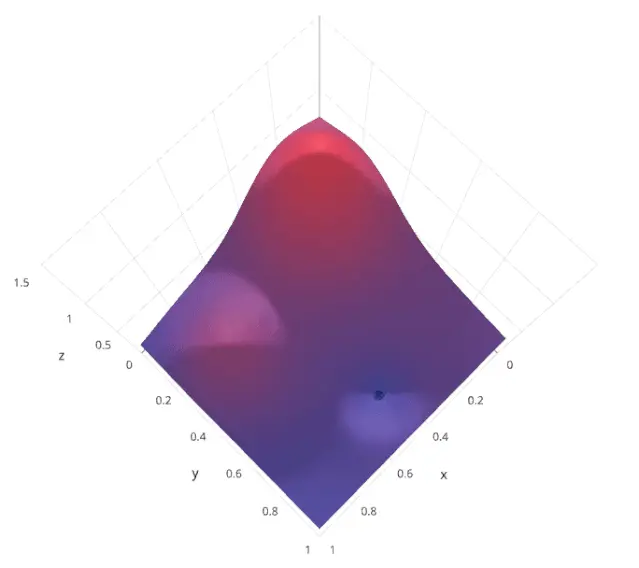
by Lavanya Gupta

2.2 优缺点分析

优点：

• 简单易理解：网格搜索方法直观且易于实现，不需要复杂的数学背景知识。
• 全面性：通过穷举搜索，可以确保找到预定义超参数空间内的全局最优解。

缺点：

• 计算成本高：随着超参数数量和取值范围的增加，组合数目会呈指数增长，导致计算成本急剧增加。
• 效率低：在很多情况下，部分超参数对模型性能影响较小，浪费了计算资源。

2.3 实践示例

以下是一个使用 Python 和 scikit-learn 库进行网格搜索的示例代码：

<code>from sklearn.model_selection import GridSearchCV

from sklearn.ensemble import RandomForestClassifier

# 定义模型和参数空间

model = RandomForestClassifier()

param_grid = {

'n_estimators': [10, 50, 100],

'max_depth': [None, 10, 20],

'min_samples_split': [2, 5, 10]

}

# 进行网格搜索

grid_search = GridSearchCV(estimator=model, param_grid=param_grid, cv=5, scoring='accuracy')code>

grid_search.fit(X_train, y_train)

# 输出最佳参数和得分

print("Best parameters found: ", grid_search.best_params_)

print("Best cross-validation score: ", grid_search.best_score_)

在这个示例中，我们对随机森林模型的三个超参数进行了网格搜索，找到了在验证集上表现最好的超参数组合。通过这种方法，我们可以显著提升模型的性能。

3. 随机搜索 (Random Search)

3.1 基本原理

随机搜索是一种超参数调优方法，通过在预定义的超参数空间内随机采样多个超参数组合，对每个组合进行模型训练和评估，找到表现最佳的超参数组合。与网格搜索不同，随机搜索不是穷举所有可能的组合，而是随机选择一部分组合进行评估。

假设我们有两个超参数 𝛼 和 𝛽，每个超参数都有多个可能的取值。随机搜索会在这些取值中随机采样若干个 (𝛼,𝛽) 组合，评估每个组合的模型性能，然后选择最优的组合。

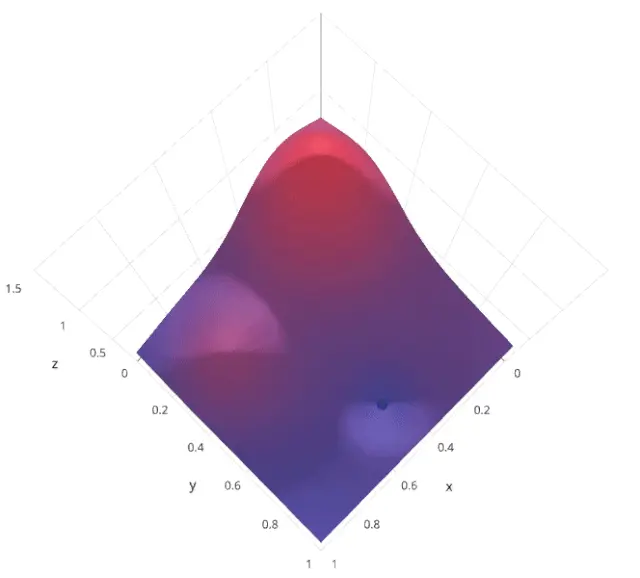
3.2 优缺点分析

优点：

• 计算成本低：随机搜索只评估部分超参数组合，计算成本比网格搜索低得多。
• 效率高：在高维超参数空间中，随机搜索通常能更快找到接近最优的超参数组合。

缺点：

• 不确定性：由于随机搜索的随机性，不同次运行可能会得到不同的结果。
• 覆盖不全面：随机搜索可能会遗漏一些表现较好的超参数组合。

3.3 实践示例

以下是一个使用 Python 和 scikit-learn 库进行随机搜索的示例代码：

<code>from sklearn.model_selection import RandomizedSearchCV

from sklearn.ensemble import RandomForestClassifier

from scipy.stats import randint

# 定义模型和参数空间

model = RandomForestClassifier()

param_dist = {

'n_estimators': randint(10, 100),

'max_depth': [None, 10, 20],

'min_samples_split': randint(2, 11)

}

# 进行随机搜索

random_search = RandomizedSearchCV(estimator=model, param_distributions=param_dist, n_iter=50, cv=5, scoring='accuracy')code>

random_search.fit(X_train, y_train)

# 输出最佳参数和得分

print("Best parameters found: ", random_search.best_params_)

print("Best cross-validation score: ", random_search.best_score_)

在这个示例中，我们对随机森林模型的三个超参数进行了随机搜索，通过随机采样的方式找到在验证集上表现最好的超参数组合。随机搜索可以在计算资源有限的情况下，快速找到接近最优的超参数组合。

4. 贝叶斯优化 (Bayesian Optimization)

4.1 基本原理

贝叶斯优化是一种智能化的超参数调优方法，通过构建一个代理模型来近似目标函数，并根据代理模型选择最优的超参数组合。具体来说，贝叶斯优化使用高斯过程或其他回归模型作为代理模型，逐步探索和利用目标函数的信息，以找到最优解。

贝叶斯优化的工作流程包括以下步骤：

1. 初始化：选择一些初始的超参数组合，计算并记录其目标函数值（如验证集上的性能）。
2. 构建代理模型：根据已评估的超参数组合和目标函数值，构建一个代理模型（如高斯过程回归）。
3. 选择下一个评估点：使用代理模型选择下一个最有希望提升目标函数值的超参数组合，通常通过最大化期望改进（EI）或其他采集函数来选择。
4. 评估目标函数：对选定的超参数组合进行模型训练和评估，记录其目标函数值。
5. 更新代理模型：将新的超参数组合和目标函数值加入训练数据，更新代理模型。
6. 重复步骤 3-5，直到满足停止条件（如评估次数达到上限或目标函数值不再显著提升）。

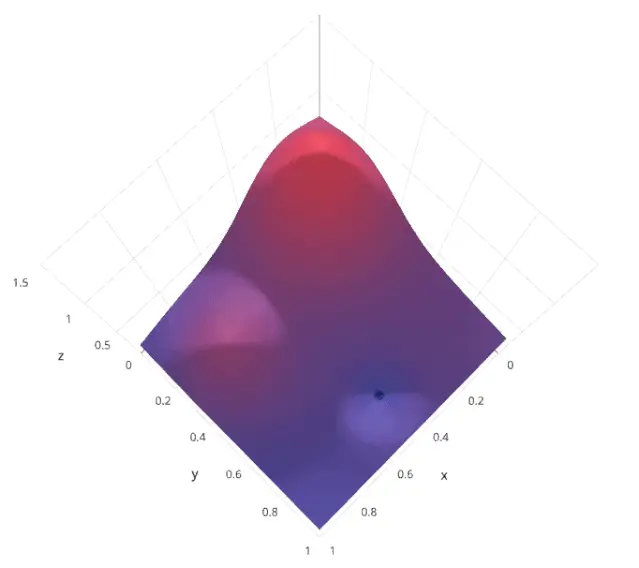
4.2 优缺点分析

优点：

• 效率高：贝叶斯优化能够智能地选择超参数组合，通常需要较少的评估次数即可找到接近最优的超参数。
• 适应性强：能够处理高维和复杂的超参数空间。

缺点：

• 实现复杂：相比网格搜索和随机搜索，贝叶斯优化的实现和调试更为复杂。
• 计算开销大：构建和更新代理模型（如高斯过程回归）在计算上可能比较昂贵。

4.3 实践示例

以下是一个使用 Python 和 scikit-optimize 库进行贝叶斯优化的示例代码：

<code>from skopt import BayesSearchCV

from sklearn.ensemble import RandomForestClassifier

# 定义模型和参数空间

model = RandomForestClassifier()

param_space = {

'n_estimators': (10, 100),

'max_depth': [None, 10, 20],

'min_samples_split': (2, 10)

}

# 进行贝叶斯优化

bayes_search = BayesSearchCV(estimator=model, search_spaces=param_space, n_iter=50, cv=5, scoring='accuracy')code>

bayes_search.fit(X_train, y_train)

# 输出最佳参数和得分

print("Best parameters found: ", bayes_search.best_params_)

print("Best cross-validation score: ", bayes_search.best_score_)

在这个示例中，我们对随机森林模型的三个超参数进行了贝叶斯优化。贝叶斯优化通过智能的采集函数选择超参数组合，能够高效地找到在验证集上表现最好的超参数组合。这种方法特别适用于复杂的超参数空间和计算资源有限的场景。

5. 遗传算法 (Genetic Algorithms)

5.1 基本原理

遗传算法是一种基于自然选择和遗传机制的优化算法，模仿生物进化过程来寻找最优解。它通过对一组候选解（即个体）进行选择、交叉和变异操作，不断生成新的解，最终找到最优的超参数组合。

遗传算法的工作流程包括以下步骤：

1. 初始化种群：随机生成一组初始的超参数组合（即种群中的个体）。
2. 适应度评估：对每个个体进行模型训练和评估，计算其适应度值（如验证集上的性能）。
3. 选择：根据适应度值选择出部分优质个体作为父代，通常使用轮盘赌选择、锦标赛选择等方法。
4. 交叉：对选定的父代进行交叉操作，生成新的个体（子代），交叉操作可以是单点交叉、多点交叉等。
5. 变异：对部分个体进行变异操作，随机改变其某些超参数值，以增加种群的多样性。
6. 生成新种群：将子代个体加入种群，并替换部分适应度较低的个体。
7. 重复步骤 2-6，直到满足停止条件（如达到最大迭代次数或适应度值不再显著提升）。

5.2 优缺点分析

优点：

• 全局搜索能力强：遗传算法通过模拟生物进化过程，能够较好地避免局部最优解，具有较强的全局搜索能力。
• 适用范围广：能够处理复杂的非线性优化问题，适用于高维和离散的超参数空间。

缺点：

• 计算成本高：每一代都需要对大量个体进行评估，计算成本较高。
• 参数设置复杂：遗传算法本身也有多个参数需要调优，如种群大小、交叉概率和变异概率等。

5.3 实践示例

以下是一个使用 Python 和 DEAP 库进行遗传算法超参数调优的示例代码：

import random

import numpy as np

from deap import base, creator, tools, algorithms

from sklearn.ensemble import RandomForestClassifier

from sklearn.model_selection import cross_val_score

# 定义适应度函数

def evaluate(individual):

n_estimators, max_depth, min_samples_split = individual

model = RandomForestClassifier(n_estimators=int(n_estimators),

max_depth=int(max_depth),

min_samples_split=int(min_samples_split))

return np.mean(cross_val_score(model, X_train, y_train, cv=5, scoring='accuracy')),code>

# 初始化遗传算法参数

toolbox = base.Toolbox()

toolbox.register("attr_int", random.randint, 10, 100)

toolbox.register("attr_none", random.choice, [None, 10, 20])

toolbox.register("attr_sample", random.randint, 2, 10)

toolbox.register("individual", tools.initCycle, creator.Individual, (toolbox.attr_int, toolbox.attr_none, toolbox.attr_sample), n=1)

toolbox.register("population", tools.initRepeat, list, toolbox.individual)

toolbox.register("mate", tools.cxTwoPoint)

toolbox.register("mutate", tools.mutUniformInt, low=[10, None, 2], up=[100, 20, 10], indpb=0.2)

toolbox.register("select", tools.selTournament, tournsize=3)

toolbox.register("evaluate", evaluate)

# 运行遗传算法

population = toolbox.population(n=50)

ngen = 20

cxpb = 0.5

mutpb = 0.2

algorithms.eaSimple(population, toolbox, cxpb, mutpb, ngen, verbose=True)

# 输出最佳参数和得分

best_individual = tools.selBest(population, k=1)[0]

print("Best parameters found: ", best_individual)

print("Best cross-validation score: ", evaluate(best_individual)[0])

在这个示例中，我们对随机森林模型的三个超参数进行了遗传算法优化。遗传算法通过模拟自然选择和遗传机制，能够高效地找到在验证集上表现最好的超参数组合。这种方法适用于需要探索复杂超参数空间的场景。

6. 模型特异化的调优策略

不同的模型类型有不同的特性，因此在进行超参数调优时，需要针对每种模型的特性选择合适的调优策略。以下是决策树模型、神经网络模型和支持向量机模型的调优策略。

6.1 决策树模型的调优

决策树模型的主要超参数包括最大深度（max_depth）、最小样本分割数（min_samples_split）和最小叶节点样本数（min_samples_leaf）等。这些超参数直接影响树的复杂度和泛化能力。

• 最大深度（max_depth）：控制树的最大深度，防止过拟合。较大的深度可能导致模型过拟合，而较小的深度可能导致欠拟合。
• 最小样本分割数（min_samples_split）：控制一个节点分裂需要的最小样本数。较大的值可以防止过拟合。
• 最小叶节点样本数（min_samples_leaf）：控制叶节点上最少的样本数，避免生成样本量过少的叶节点，从而防止过拟合。

调优策略通常是通过网格搜索或随机搜索来找到最佳参数组合。以下是一个示例：

from sklearn.model_selection import GridSearchCV

from sklearn.tree import DecisionTreeClassifier

model = DecisionTreeClassifier()

param_grid = {

'max_depth': [None, 10, 20, 30],

'min_samples_split': [2, 5, 10],

'min_samples_leaf': [1, 2, 4]

}

grid_search = GridSearchCV(estimator=model, param_grid=param_grid, cv=5, scoring='accuracy')code>

grid_search.fit(X_train, y_train)

print("Best parameters found: ", grid_search.best_params_)

print("Best cross-validation score: ", grid_search.best_score_)

6.2 神经网络模型的调优

神经网络模型的超参数包括层数和每层的神经元数量、学习率（learning_rate）、批次大小（batch_size）和训练轮数（epochs）等。这些超参数决定了模型的容量和训练效率。

• 层数和神经元数量：控制模型的容量，较多的层数和神经元数量可以增加模型的表达能力，但也可能导致过拟合。
• 学习率（learning_rate）：控制权重更新的步长，较大的学习率可能导致训练不稳定，而较小的学习率可能使训练过慢。
• 批次大小（batch_size）：控制每次更新模型参数时使用的样本数，较大的批次大小可以使训练更加稳定，但会增加内存开销。
• 训练轮数（epochs）：控制整个训练集被使用的次数，适当的训练轮数可以确保模型充分学习，但过多的训练轮数可能导致过拟合。

调优策略可以使用随机搜索或贝叶斯优化来找到最佳参数组合。以下是一个示例：

from keras.models import Sequential

from keras.layers import Dense

from keras.wrappers.scikit_learn import KerasClassifier

from sklearn.model_selection import RandomizedSearchCV

def create_model(neurons=1, learning_rate=0.01):

model = Sequential()

model.add(Dense(neurons, input_dim=X_train.shape[1], activation='relu'))code>

model.add(Dense(1, activation='sigmoid'))code>

model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['accuracy'])code>

return model

model = KerasClassifier(build_fn=create_model, epochs=100, batch_size=10, verbose=0)

param_dist = {

'neurons': [10, 20, 30, 40, 50],

'learning_rate': [0.001, 0.01, 0.1]

}

random_search = RandomizedSearchCV(estimator=model, param_distributions=param_dist, n_iter=10, cv=5, scoring='accuracy')code>

random_search.fit(X_train, y_train)

print("Best parameters found: ", random_search.best_params_)

print("Best cross-validation score: ", random_search.best_score_)

6.3 支持向量机的调优

支持向量机（SVM）的主要超参数包括惩罚参数（C）、核函数类型（kernel）和核函数的参数（如 RBF 核的 gamma 值）等。这些超参数决定了模型的边界和泛化能力。

• 惩罚参数（C）：控制误分类样本的惩罚力度，较大的值会尝试正确分类所有训练样本，但可能导致过拟合，较小的值会允许更多误分类，但能增加模型的泛化能力。
• 核函数类型（kernel）：如线性核、RBF 核、多项式核等，不同的核函数适用于不同的数据分布。
• 核函数的参数（如 gamma）：控制样本影响范围，较大的 gamma 值会使每个样本的影响范围较小，模型更复杂，较小的 gamma 值会使影响范围更大，模型更简单。

调优策略通常通过网格搜索或随机搜索找到最佳参数组合。以下是一个示例：

from sklearn.model_selection import GridSearchCV

from sklearn.svm import SVC

model = SVC()

param_grid = {

'C': [0.1, 1, 10, 100],

'kernel': ['linear', 'rbf', 'poly'],

'gamma': [0.001, 0.01, 0.1, 1]

}

grid_search = GridSearchCV(estimator=model, param_grid=param_grid, cv=5, scoring='accuracy')code>

grid_search.fit(X_train, y_train)

print("Best parameters found: ", grid_search.best_params_)

print("Best cross-validation score: ", grid_search.best_score_)

通过针对不同模型类型的特异化调优策略，可以显著提升模型的性能，使其更好地适应具体问题。

7. 超参数优化库

使用专门的超参数优化库，可以更高效地进行超参数调优。这些库提供了多种优化方法和工具，方便用户快速找到最优的超参数组合。以下介绍三个常用的超参数优化库：Hyperopt、Optuna 和其他流行库。

7.1 Hyperopt

Hyperopt 是一个开源的 Python 库，用于高效地进行超参数优化。它支持随机搜索、TPE（Tree-structured Parzen Estimator）和基于贝叶斯优化的方法。Hyperopt 的主要优点是简单易用，并且能够处理大规模搜索空间。

以下是一个使用 Hyperopt 进行超参数优化的示例：

from hyperopt import fmin, tpe, hp, Trials

from sklearn.ensemble import RandomForestClassifier

from sklearn.model_selection import cross_val_score

# 定义搜索空间

space = {

'n_estimators': hp.choice('n_estimators', range(10, 101)),

'max_depth': hp.choice('max_depth', [None, 10, 20, 30]),

'min_samples_split': hp.choice('min_samples_split', range(2, 11))

}

# 定义目标函数

def objective(params):

model = RandomForestClassifier(**params)

score = cross_val_score(model, X_train, y_train, cv=5, scoring='accuracy').mean()code>

return -score

# 进行优化

trials = Trials()

best = fmin(fn=objective, space=space, algo=tpe.suggest, max_evals=50, trials=trials)

print("Best parameters found: ", best)

7.2 Optuna

Optuna 是一个高效且灵活的超参数优化库，支持网格搜索、随机搜索和贝叶斯优化等方法。Optuna 的特点是其动态采样和早停功能，可以显著加快优化过程。

以下是一个使用 Optuna 进行超参数优化的示例：

import optuna

from sklearn.ensemble import RandomForestClassifier

from sklearn.model_selection import cross_val_score

# 定义目标函数

def objective(trial):

n_estimators = trial.suggest_int('n_estimators', 10, 100)

max_depth = trial.suggest_categorical('max_depth', [None, 10, 20, 30])

min_samples_split = trial.suggest_int('min_samples_split', 2, 10)

model = RandomForestClassifier(n_estimators=n_estimators, max_depth=max_depth, min_samples_split=min_samples_split)

score = cross_val_score(model, X_train, y_train, cv=5, scoring='accuracy').mean()code>

return score

# 进行优化

study = optuna.create_study(direction='maximize')code>

study.optimize(objective, n_trials=50)

print("Best parameters found: ", study.best_params)

print("Best cross-validation score: ", study.best_value)

7.3 其他流行库介绍

除了 Hyperopt 和 Optuna，还有一些其他流行的超参数优化库，包括：

• Scikit-Optimize（skopt）：提供贝叶斯优化、随机搜索和网格搜索等方法，易于与 scikit-learn 集成。
• Spearmint：专注于贝叶斯优化，适用于复杂的高维搜索空间。
• Ray Tune：支持大规模分布式超参数优化，适用于需要高并发和大规模计算的场景。

通过使用这些优化库，用户可以更高效地进行超参数调优，提升模型性能。

8. 实践中的超参数调优技巧

在实际应用中，超参数调优不仅是选择合适的方法和库，还需要一些技巧来提升调优效率和效果。以下介绍一些在实践中常用的调优技巧，包括如何选择合适的调优方法、调优不同类型的模型，以及常见的调优陷阱与解决方案。

8.1 如何选择合适的调优方法

选择合适的超参数调优方法取决于多个因素，包括问题的复杂度、数据集大小、可用计算资源等。以下是一些指导原则：

• 问题复杂度和计算资源：对于简单的问题和有限的计算资源，网格搜索和随机搜索是较好的选择。对于复杂的问题和充足的计算资源，贝叶斯优化和遗传算法可能更有效。
• 数据集大小：对于大数据集，分布式调优方法（如 Ray Tune）可以有效利用多台机器的计算能力，提高调优效率。
• 模型类型：不同模型对超参数的敏感性不同，需要针对具体模型选择合适的调优方法。例如，神经网络通常适合使用随机搜索或贝叶斯优化，而树模型（如随机森林、梯度提升树）适合使用网格搜索或随机搜索。

8.2 实例：调优不同类型的模型

以下是调优不同类型模型的一些实例：

• 线性回归模型：调优超参数包括正则化参数（如 L1 和 L2 正则化系数）。可以使用网格搜索或随机搜索。

from sklearn.linear_model import Ridge

from sklearn.model_selection import GridSearchCV

model = Ridge()

param_grid = {'alpha': [0.1, 1, 10, 100]}

grid_search = GridSearchCV(estimator=model, param_grid=param_grid, cv=5, scoring='neg_mean_squared_error')code>

grid_search.fit(X_train, y_train)

print("Best parameters found: ", grid_search.best_params_)

print("Best cross-validation score: ", grid_search.best_score_)

• 决策树模型：调优超参数包括最大深度、最小样本分割数和最小叶节点样本数。可以使用网格搜索或随机搜索。

from sklearn.tree import DecisionTreeRegressor

from sklearn.model_selection import RandomizedSearchCV

model = DecisionTreeRegressor()

param_dist = {'max_depth': [None, 10, 20, 30], 'min_samples_split': [2, 5, 10], 'min_samples_leaf': [1, 2, 4]}

random_search = RandomizedSearchCV(estimator=model, param_distributions=param_dist, n_iter=50, cv=5, scoring='neg_mean_squared_error')code>

random_search.fit(X_train, y_train)

print("Best parameters found: ", random_search.best_params_)

print("Best cross-validation score: ", random_search.best_score_)

• 神经网络模型：调优超参数包括层数、神经元数量、学习率、批次大小和训练轮数。可以使用随机搜索或贝叶斯优化。

from keras.models import Sequential

from keras.layers import Dense

from keras.wrappers.scikit_learn import KerasRegressor

from sklearn.model_selection import RandomizedSearchCV

def create_model(neurons=1, learning_rate=0.01):

model = Sequential()

model.add(Dense(neurons, input_dim=X_train.shape[1], activation='relu'))code>

model.add(Dense(1))

model.compile(optimizer='adam', loss='mean_squared_error')code>

return model

model = KerasRegressor(build_fn=create_model, epochs=100, batch_size=10, verbose=0)

param_dist = {'neurons': [10, 20, 30, 40, 50], 'learning_rate': [0.001, 0.01, 0.1]}

random_search = RandomizedSearchCV(estimator=model, param_distributions=param_dist, n_iter=10, cv=5, scoring='neg_mean_squared_error')code>

random_search.fit(X_train, y_train)

print("Best parameters found: ", random_search.best_params_)

print("Best cross-validation score: ", random_search.best_score_)

8.3 常见的调优陷阱与解决方案

在进行超参数调优时，可能会遇到一些常见的陷阱和问题，以下是几种常见陷阱及其解决方案：

• 过拟合：在训练集上表现很好，但在验证集上表现差。解决方案是增加正则化或减少模型复杂度。
• 欠拟合：在训练集和验证集上都表现差。解决方案是增加模型复杂度或调整超参数。
• 高维搜索空间：超参数维度太多，导致调优效率低。解决方案是使用贝叶斯优化或遗传算法来高效搜索。
• 计算资源不足：计算资源有限，无法进行大量评估。解决方案是使用随机搜索或分布式调优方法。

通过掌握这些技巧，可以更高效地进行超参数调优，提升模型性能，避免常见问题。

9. 高级调优技术

在超参数调优领域，有一些更为高级的技术可以进一步提升调优效果和效率。这些技术包括多目标优化、异步并行优化和集成学习中的调优。掌握这些高级技术可以帮助我们在复杂的模型和大规模数据集上进行更精细的调优。

9.1 多目标优化

多目标优化是一种同时优化多个目标函数的方法。通常在机器学习中，我们不仅希望提高模型的准确性，还希望控制模型的复杂度、减少训练时间等。多目标优化可以帮助我们在这些目标之间找到最佳平衡。

• 帕累托最优解：多目标优化的结果通常是一个帕累托前沿（Pareto Front），其中每个解在一个目标上没有其他解更优，同时在另一个目标上也没有更劣。
• 应用：在神经网络中，我们可能希望同时最小化训练误差和模型参数数量。多目标优化可以找到在这两个目标上均表现较好的解。

示例代码：

import optuna

def objective(trial):

n_layers = trial.suggest_int('n_layers', 1, 3)

dropout_rate = trial.suggest_float('dropout_rate', 0.0, 0.5)

lr = trial.suggest_loguniform('lr', 1e-5, 1e-1)

# 模型定义和训练

# ...

accuracy = 0.9 # 假设的准确性结果

complexity = n_layers * 1000 # 假设的复杂度结果

return accuracy, complexity

study = optuna.create_study(directions=['maximize', 'minimize'])

study.optimize(objective, n_trials=50)

for trial in study.best_trials:

print(trial.values, trial.params)

9.2 异步并行优化

异步并行优化是一种在多台机器或多线程上并行进行超参数调优的方法，可以显著加快调优速度。异步并行优化允许多个调优任务同时进行，而不需要等待所有任务完成才能开始新的任务。

• 分布式计算：在大规模数据集和复杂模型中，异步并行优化可以利用多台机器或多个 GPU 并行处理，提高调优效率。
• 早停策略：结合早停策略，可以在发现某个超参数组合表现不佳时提前停止该任务，节省计算资源。

示例代码：

import ray

from ray import tune

def train_model(config):

# 模型定义和训练

# ...

tune.report(mean_accuracy=accuracy)

ray.init()

analysis = tune.run(

train_model,

config={

"n_estimators": tune.randint(10, 100),

"max_depth": tune.choice([None, 10, 20, 30]),

"min_samples_split": tune.randint(2, 11)

},

num_samples=50,

resources_per_trial={"cpu": 1, "gpu": 0}

)

print("Best hyperparameters found were: ", analysis.best_config)

9.3 集成学习中的调优

集成学习通过结合多个基模型的预测结果来提升整体模型的性能。在集成学习中，超参数调优同样重要，可以通过调优基模型和集成方法的超参数来提高集成模型的表现。

• 基模型调优：对每个基模型进行独立的超参数调优，以找到最优的基模型组合。
• 集成方法调优：调优集成方法的超参数，如随机森林中的树数量、梯度提升中的学习率和弱学习器数量等。

示例代码：

from sklearn.ensemble import RandomForestClassifier, GradientBoostingClassifier

from sklearn.model_selection import GridSearchCV

# 基模型调优

rf_param_grid = {'n_estimators': [10, 50, 100], 'max_depth': [None, 10, 20]}

rf_grid_search = GridSearchCV(estimator=RandomForestClassifier(), param_grid=rf_param_grid, cv=5)

rf_grid_search.fit(X_train, y_train)

gb_param_grid = {'n_estimators': [10, 50, 100], 'learning_rate': [0.01, 0.1, 0.2]}

gb_grid_search = GridSearchCV(estimator=GradientBoostingClassifier(), param_grid=gb_param_grid, cv=5)

gb_grid_search.fit(X_train, y_train)

# 集成方法调优

best_rf = rf_grid_search.best_estimator_

best_gb = gb_grid_search.best_estimator_

ensemble_model = VotingClassifier(estimators=[('rf', best_rf), ('gb', best_gb)], voting='soft')code>

ensemble_model.fit(X_train, y_train)

print("Ensemble model score: ", ensemble_model.score(X_test, y_test))

通过掌握这些高级调优技术，可以更高效地提升模型性能，解决复杂的优化问题。在实际应用中，选择合适的调优方法和技巧是关键。

[ 抱个拳，总个结 ]

在这篇文章中，我们详细介绍了超参数调优的基本概念和几种常用的方法。以下是一些关键要点的简要回顾：

• 超参数与模型参数的区别：超参数是由用户手动设定的，不能通过训练数据自动学习得来。它们直接影响模型的性能和训练效率。
• 网格搜索：通过穷举搜索预定义的超参数空间，找到最佳的超参数组合。优点是全面性，缺点是计算成本高。
• 随机搜索：通过在超参数空间内随机采样，找到表现最佳的超参数组合。优点是计算成本低，效率高，缺点是结果具有不确定性。
• 贝叶斯优化：通过构建代理模型来近似目标函数，并根据代理模型选择最优的超参数组合。优点是效率高，适应性强，缺点是实现复杂。
• 遗传算法：模仿生物进化过程，通过选择、交叉和变异操作，不断生成新的超参数组合，找到最优解。优点是全局搜索能力强，适用范围广，缺点是计算成本高，参数设置复杂。
• 模型特异化的调优策略：针对不同模型（如决策树、神经网络、支持向量机）有不同的调优策略。
• 超参数优化库：介绍了 Hyperopt、Optuna 和其他流行库，使用这些库可以更高效地进行超参数调优。
• 实践中的超参数调优技巧：包括如何选择合适的调优方法、调优不同类型的模型，以及常见的调优陷阱与解决方案。
• 高级调优技术：包括多目标优化、异步并行优化和集成学习中的调优，这些技术可以进一步提升调优效果和效率。

通过掌握这些超参数调优的方法和技巧，大侠们可以更高效地提升模型性能，解决复杂的优化问题。希望这篇文章能为大家提供有价值的参考，助力于实践中的超参数调优工作。

- 科研为国分忧，创新与民造福 -

日更时间紧任务急，难免有疏漏之处，还请大侠海涵内容仅供学习交流之用，部分素材来自网络，侵联删

[ 算法金，碎碎念 ]

全网同名，日更万日，让更多人享受智能乐趣

如果觉得内容有价值，烦请大侠多多 分享、在看、点赞，助力算法金又猛又持久、很黄很 BL 的日更下去；

同时邀请大侠 关注、星标 算法金，围观日更万日，助你功力大增、笑傲江湖