Fast Planner规划算法（一）—— Fast Planner前端

慕羽★ 2024-08-15 10:03:01 阅读 70

本系列文章用于回顾学习记录Fast-Planner规划算法的相关内容，【本系列博客写于2023年9月，共包含四篇文章，现在进行补发第一篇，其余几篇文章将在近期补发】

一、Fast Planner前端

Fast Planner的轨迹规划部分一共分为三个模块，前端采用Hybrid A* 算法生成比较粗糙的路径\轨迹，然后采用后端对前端生成的路径进行更加细致的处理和优化。

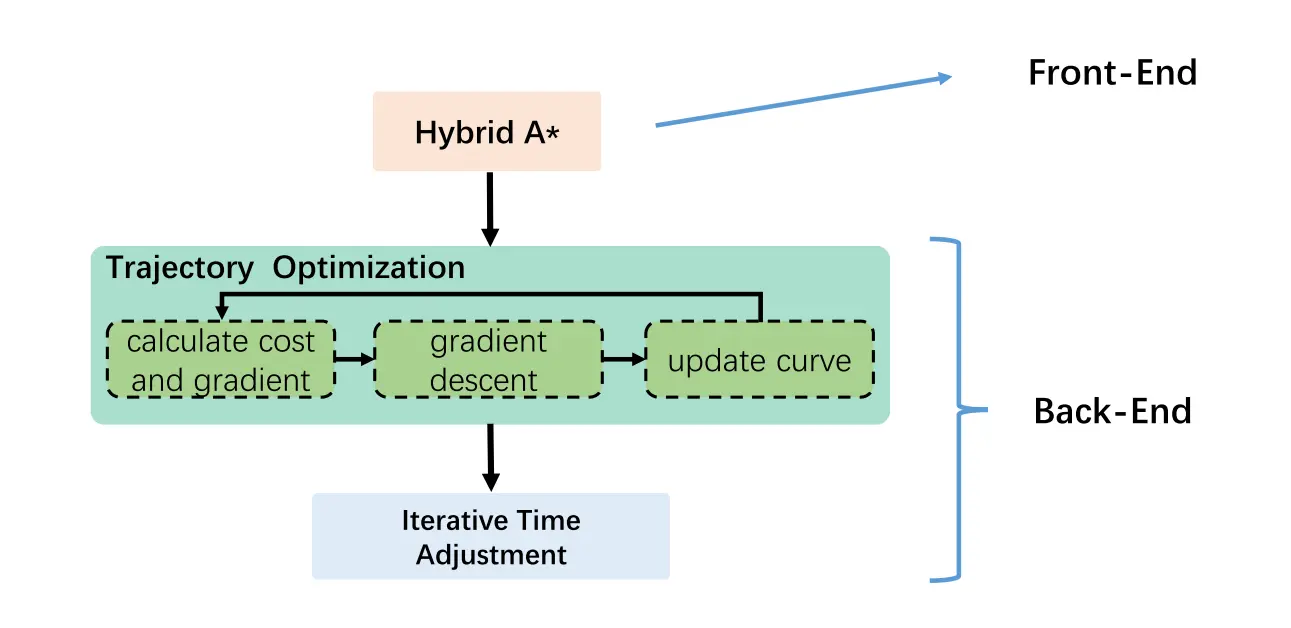
在这里插入图片描述

本部分内容对前端进行介绍，Hybrid A* 算法的原理在前面的文章中已经介绍过了，这里主要介绍在Fast Planner中具体使用的一些流程和细节。

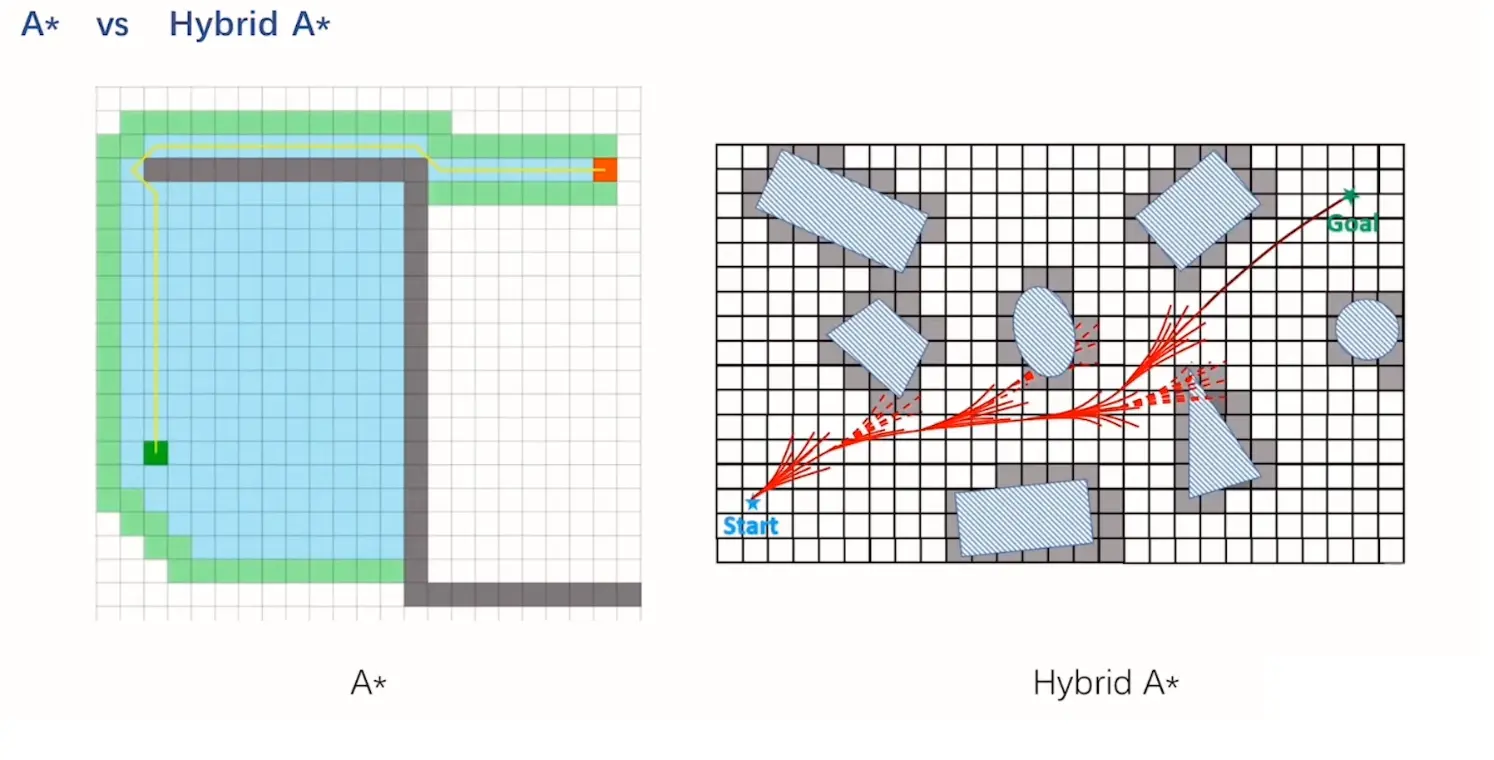
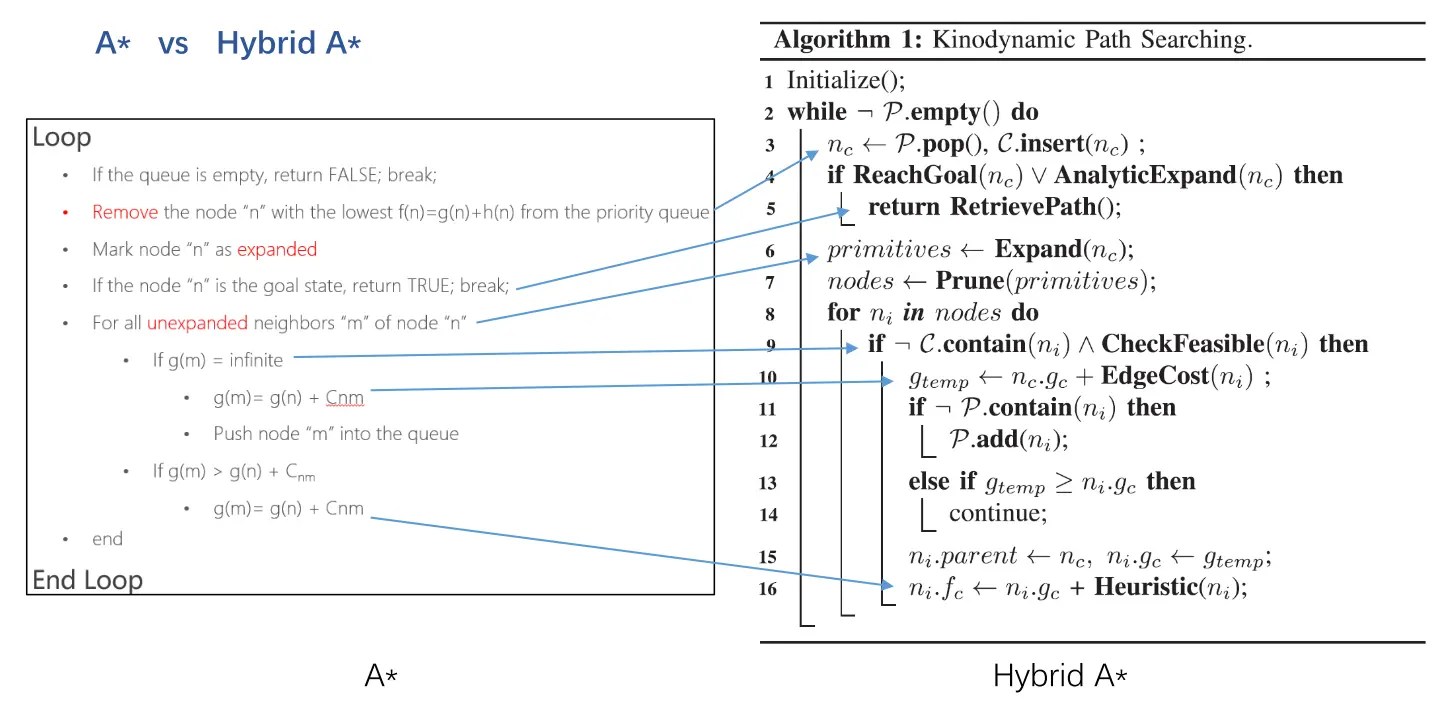
在这里插入图片描述

Fast Planner中 Hybrid A* 算法的主要流程如下：

在每轮循环中，首先会从优先队列中拿出新的节点

n_c

nc，并判断该节点是否为终点以及从该节点能不能直接生成到终点的路径（比如采用Reeds sheep算法），若是，则规划结束返回路径，若不是则继续进行本轮循环

在该新节点

n_c

nc处向外拓展生成一些小的轨迹，这些小轨迹称为primitive，它们的末端就是拓展出来的节点，然后进行剪枝操作，如果有多个节点落在同一个栅格中，仅保留一个，讲这些新拓展出来的节点存放在nodes中。

然后对nodes中的每个节点的质量进行评估（伪代码8-16行），对于每个节点，首先检查其是否已经在已经拓展过的闭集合中以及是否是可行节点(在边界范围内、不与障碍物碰撞等)，

若在闭集合或不是可行节点，则结束对这个节点的评估，继续进行下一个节点的评估。若不在闭集合中且为可行节点，则继续进行该节点的评估，计算该节点的g值，即其父节点

n_c

nc的g值加上该节点对应的小轨迹的代价值。然后判断该节点是否在待拓展的开集合中，若不在，则将其加入到开集合中，记录该节点的g值以及父节点，并计算该节点的f值，该节点的评估结束，若已经在开集合中了，则判断该节点上面算出的新g值是否大于原有的g值，若是则不需要进行处理（该节点原有的方案更优），继续评估下一个节点，若不是，则说明该节点的现有方案更优，将该节点的父节点更新为

n_c

nc，g值更新为新的g值，并更新计算该节点的总代价f值。本节点评估结束，继续评估下一个节点。

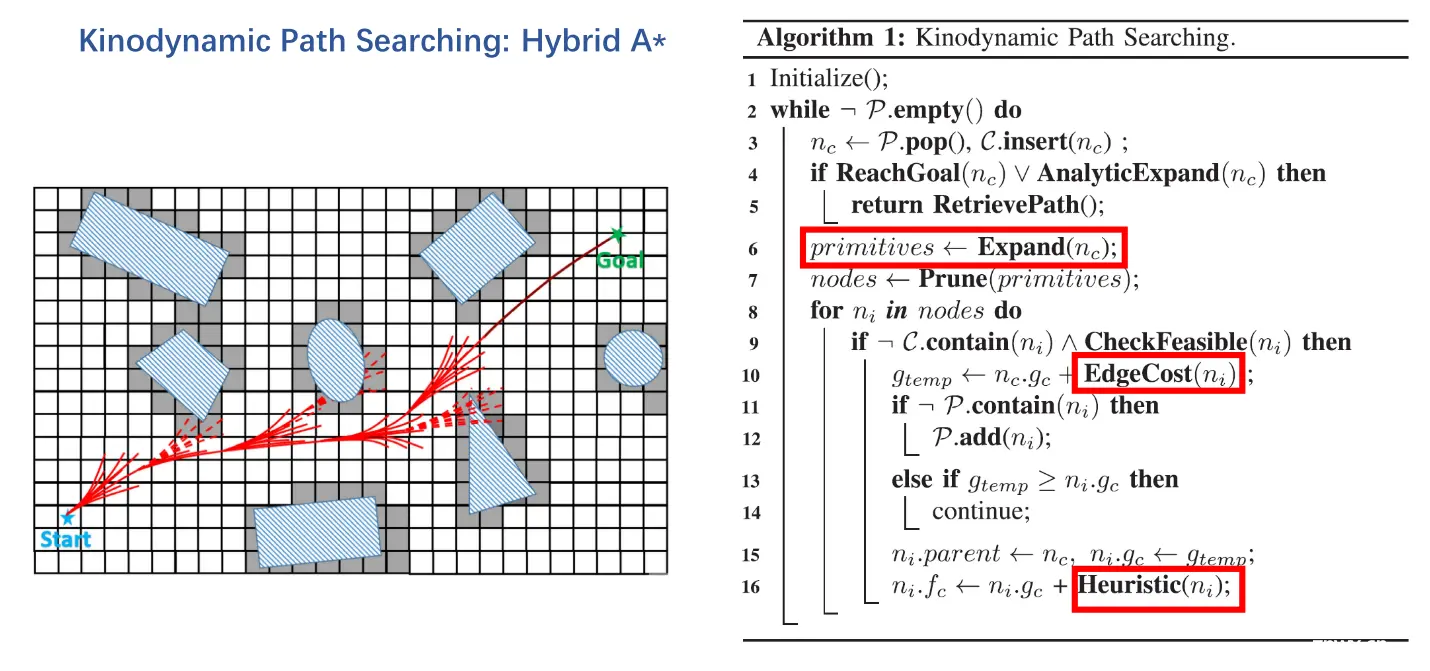
在这里插入图片描述

下面来详细看一下上面流程中的一些具体细节：

【注：Hybrid A * 算法每个具体执行过程的实现都有很多种方法，在前面的文章中，我们给出了 zhm_real/MotionPlanning运动规划库中的实现方法及细节，这里给出Fast Planner中的具体实现细节】

（1）、如何由节点

n_c

nc拓展生成小轨迹primitive——对应Expend函数

将x，y、z轴的轨迹用三个独立的多项式来表示，比如用二次多项式

(

)

p_x(t)=a_0+a_1t+a_2t^2

px(t)=a0+a1t+a2t2，自变量是时间t，则状态量和控制输入量可表示成以下的形式

(

)

[

(

)

(

)

(

−

)

(

)

]

⊂

(

)

(

)

(

)

∈

[

−

]

⊂

\begin{aligned}&\mathbf{x}(t):=\boxed{\left[\mathbf{p}(t)^{\mathrm{T}}, \mathbf{\dot p}(t)^{\mathrm{T}},...,\mathbf{p}^{(n-1)}(t)^{\mathrm{T}}\right]^{\mathrm{T}}}\subset\mathbb{R}^{3n}\\&\mathbf{u}(t):=\mathbf{p}^{(n)}(t)\in\mathcal{U}:=[-u_{max},u_{max}]^3\subset\mathbb{R}^3\end{aligned}

x(t):=[p(t)T,p˙(t)T,...,p(n−1)(t)T]T⊂R3nu(t):=p(n)(t)∈U:=[−umax,umax]3⊂R3

然后，我们就可以写出状态空间方程，

[

⋯

⋮

⋱

⋮

⋯

]

[

⋮

]

\begin{gathered}\dot{\mathbf{x}}=\mathbf{A}\mathbf{x}+\mathbf{B}\mathbf{u}\\\mathbf{A}=\begin{bmatrix}0&\mathbf{I}_3&\mathbf{0}&\cdots&\mathbf{0}\\\mathbf{0}&\mathbf{0}&\mathbf{I}_3&\cdots&\mathbf{0}\\\varvdots&\varvdots&\varvdots&\ddots&\varvdots\\\mathbf{0}&\cdots&\cdots&\mathbf{0}&\mathbf{I}_3\\\mathbf{0}&\cdots&\cdots&\mathbf{0}&\mathbf{0}\end{bmatrix},\mathbf{B}=\begin{bmatrix}\mathbf{0}\\\mathbf{0}\\\varvdots\\\mathbf{0}\\\mathbf{I}_3\end{bmatrix}\end{gathered}

x˙=Ax+BuA=

00⋮00I30⋮⋯⋯0I3⋮⋯⋯⋯⋯⋱0000⋮I30

,B=

00⋮0I3

这样，我们给定一个初始状态和一段时间内的控制输入里以后，就可以利用下式计算整条小轨迹上任意时刻的状态

(

)

(

)

∫

(

−

)

(

)

initial state

control input

\begin{aligned}\mathbf{x}(t)=e^{\mathbf{A}t}&\color{red}{\boxed{\mathbf{x}(0)}}+\color{black}\int_0^te^{\mathbf{A}(t-\tau)}\mathbf{B}&\color{red}{\boxed{\mathbf{u}(\tau)}}\color{black} d\tau\\&\color{red}{\text{initial state}}&\color{red}{\text{control input}}\end{aligned}

x(t)=eAtx(0)+∫0teA(t−τ)Binitial stateu(τ)dτcontrol input

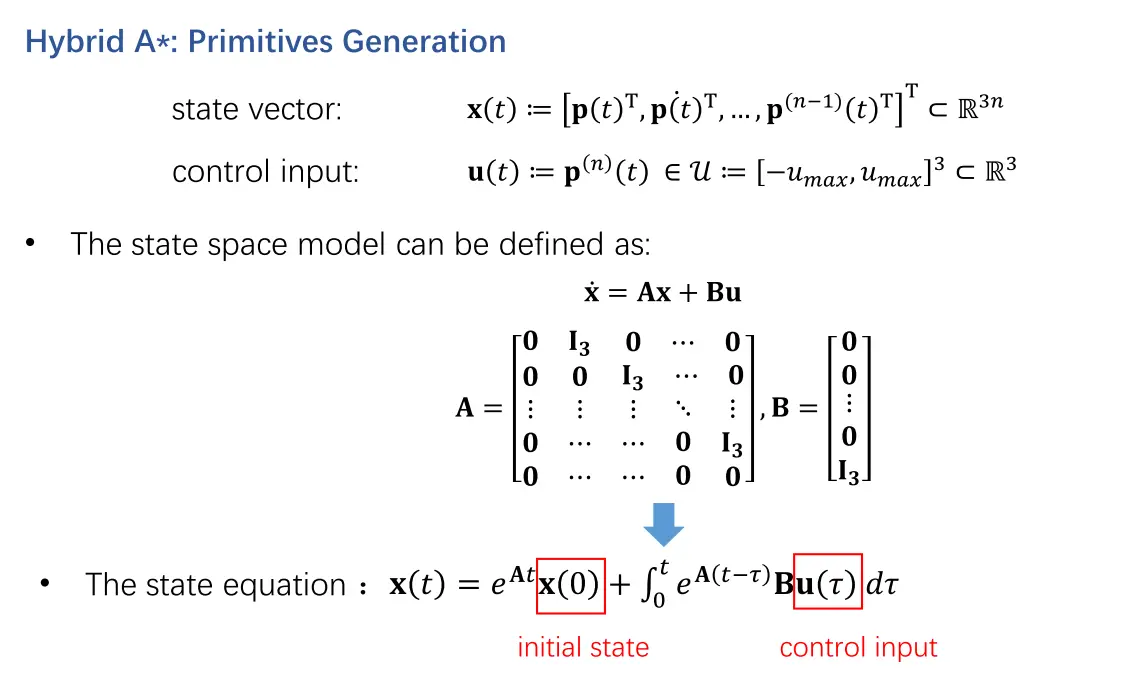
在这里插入图片描述

实际使用时，会对控制量在上下界范围内进行平均的离散采样，得到多组控制输入量，从而得到多条小轨迹

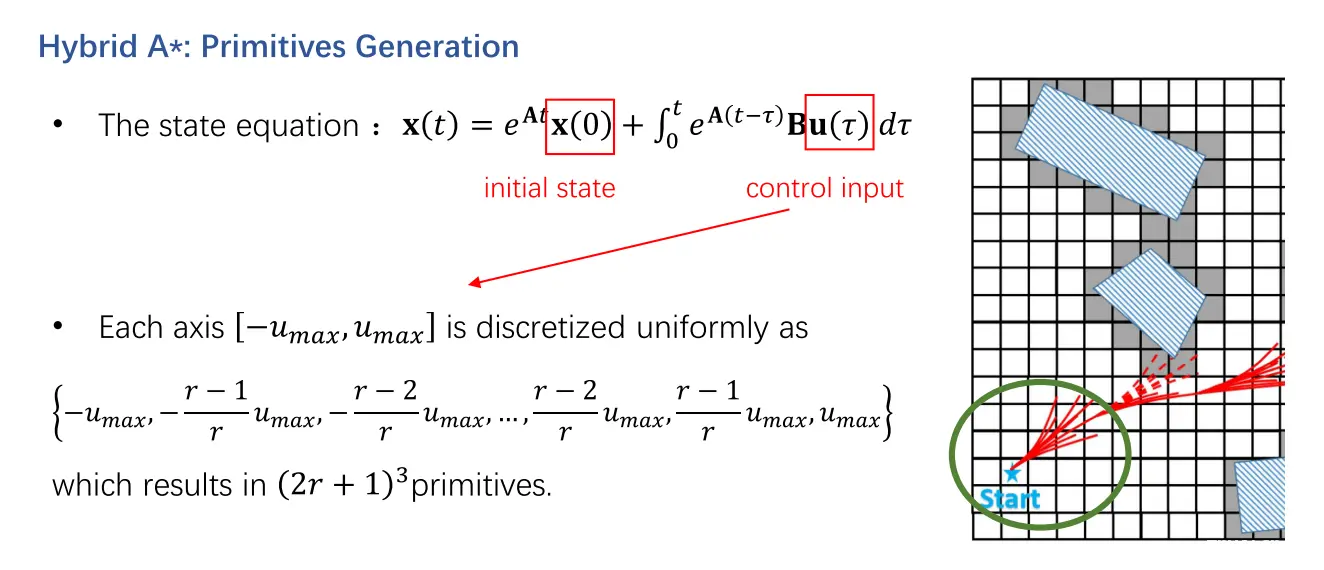
在这里插入图片描述

在Fast-Planner中，n取值为2，即状态选取为位置和速度，输入为加速度

在这里插入图片描述

（2）、如何计算每段小轨迹的代价值——对应EdgeCost函数

对于一条小轨迹，在Fast-Planner中我们比较在意的是这条轨迹的执行时间和控制量，所以定义如下的代价函数（不同的需求和实际应用场景，可以选择不同的代价函数）

(

)

∫

∥

(

)

∥

T(T)=\int_{0}^{T}\|\mathbf{u}(t)\|^{2}dt+\rho T

T(T)=∫0T∥u(t)∥2dt+ρT

其中

T表示这一段小轨迹的时间，

u是控制量，

\rho

ρ表示对时间惩罚项的权重参数，对于一条小轨迹而言，在0~T时间内它的控制输入是固定的常量，每条小轨迹的总时间T也是固定的，所以，我们并不需要计算上面的积分，它等效于使用下式来计算小轨迹的代价值，

\tau

τ即为小轨迹的持续时间

(

∥

)

e_{c}=(\|\mathbf{u}_{d}\|^{2}+\rho)\tau

ec=(∥ud∥2+ρ)τ

然后，我们把从起点开始的到当前节点的所有小轨迹的代价加起来，就得到了，从起点到当前节点的代价值，也就是该节点的g值，如下所示：

∑

(

∥

(

)

∥

)

g_c=\sum_{j=1}^J\left(\left\|(\mathbf{u}_d)_j\right\|^2+\rho\right)\tau

gc=j=1∑J(∥(ud)j∥2+ρ)τ

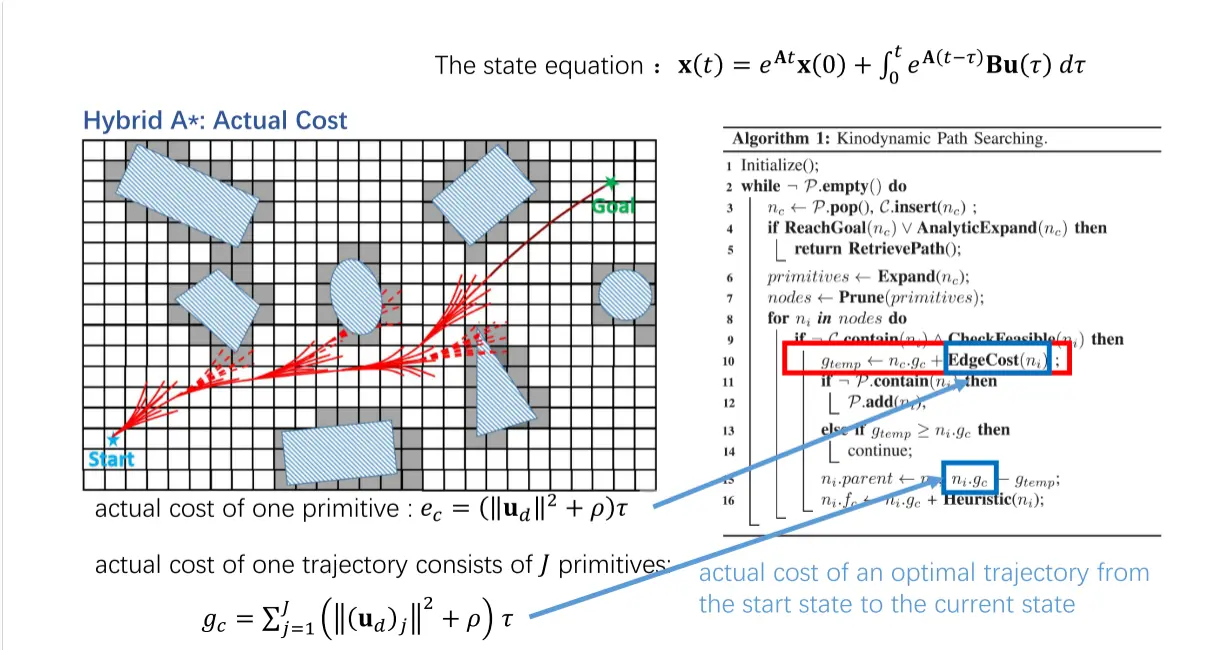
在这里插入图片描述

（3）、如何评估一个节点的启发代价值——对应Heuristic函数

基于庞特里亚金最小原理设计了一条三阶的多项式轨迹，从当前状态出发，终止于目标点，轨迹的总时长已知，给定当前点和目标点的位置和速度，如下所示：

(

)

(

)

(

)

(

)

(

)

\begin{aligned}p(t)&=a_3t^3+a_2t^2+a_1t+a_0\\p(0)&=p_{\mu c},\quad p(\dot{0})=v_{\mu c}\\p(T)&=p_{\mu g},\quad p(\dot{T})=v_{\mu g}\end{aligned}

p(t)p(0)p(T)=a3t3+a2t2+a1t+a0=pμc,p(0˙)=vμc=pμg,p(T˙)=vμg

因此，可以得到该多项式系数满足下式：

[

]

[

]

[

]

\begin{bmatrix}0&0&0&1\\0&0&1&0\\T^3&T^2&T&1\\3T^2&2T&1&0\end{bmatrix}\begin{bmatrix}a_3\\a_2\\a_1\\a_0\end{bmatrix}=\begin{bmatrix}p_{\mu c}\\v_{\mu c}\\p_{\mu g}\\v_{\mu g}\end{bmatrix}

00T33T200T22T01T11010

a3a2a1a0

pμcvμcpμgvμg

然后，基于庞特里亚金最小原理，得到最优的轨迹表达式如下：

∗

(

)

[

]

[

−

]

[

−

]

\begin{aligned}p_\mu^*(t)&=\frac{1}{6}\alpha_\mu t^3+\frac{1}{2}\beta_\mu t^2+v_{\mu c}t+p_{\mu c}\\\\\begin{bmatrix}\alpha_\mu\\\beta_\mu\end{bmatrix}&=\frac{1}{T^3}\begin{bmatrix}-12&6T\\6T&-2T^2\end{bmatrix}\begin{bmatrix}p_{\mu g}-p_{\mu c}-v_{\mu c}T\\v_{\mu g}-v_{\mu c}\end{bmatrix}\end{aligned}

pμ∗(t)[αμβμ]=61αμt3+21βμt2+vμct+pμc=T31[−126T6T−2T2][pμg−pμc−vμcTvμg−vμc]

得到上面的位置轨迹后，求两阶导数可以得到加速度轨迹，在取位置和速度为状态量时，加速度也即控制输入：

∗

(

)

(

)

[

(

)

(

)

(

)

]

\begin{aligned}&a_\mu^*(t)=\alpha_\mu t+\beta_\mu\\\\&\mathbf{u}(t):=[a_x(t),a_y(t),a_z(t)]^\mathrm{T}\end{aligned}

aμ∗(t)=αμt+βμu(t):=[ax(t),ay(t),az(t)]T

得到了这样一条轨迹后，就可以利用上面介绍的求小轨迹的代价的方式，求出这条轨迹的代价，作为考虑运动学但不考虑障碍物的启发式代价函数。

∗

(

)

∫

∥

(

)

∥

∑

∈

{

}

(

)

\begin{aligned} \mathcal{T}^{*}(T)& =\int_{0}^{l}\|\mathbf{u}(t)\|^{2}dt+\rho T \\ &=\sum_{\mu\in\{x,y,z\}}\left(\frac{1}{3}{\alpha_{\mu}}^{2}T^{3}+\frac{1}{2}\alpha_{\mu}\beta_{\mu}T^{2}+{\beta_{\mu}}^{2}T\right)+\rho T \end{aligned}

T∗(T)=∫0l∥u(t)∥2dt+ρT=μ∈{ x,y,z}∑(31αμ2T3+21αμβμT2+βμ2T)+ρT

上面，我们假设时间T是人为给定的、已知的，但是很明显，我们并不清楚，从当前点到目标点合适的T应该如何选择。所以，我们可以将上式对T进行求导等于0，即

∂

∗

(

)

∂

\frac{\partial\mathcal{T}^*(T)}{\partial T}=0

∂T∂T∗(T)=0，来求取最合适的

T_h

Th，进而得到代价值

在这里插入图片描述