文章目录

1. 源码分析2. 调整红黑树的结构搭建map、set3. 红黑树的迭代器3.1 普通迭代器3.2 const迭代器3.3 map的operator[ ]

4. 完整代码4.1 RBTree4.2 MyMap4.3 MySet

对于map与set，它们一个是KV模型，一个是K模型，那我们要写两个红黑树吗？

我们来看一下源码

1. 源码分析

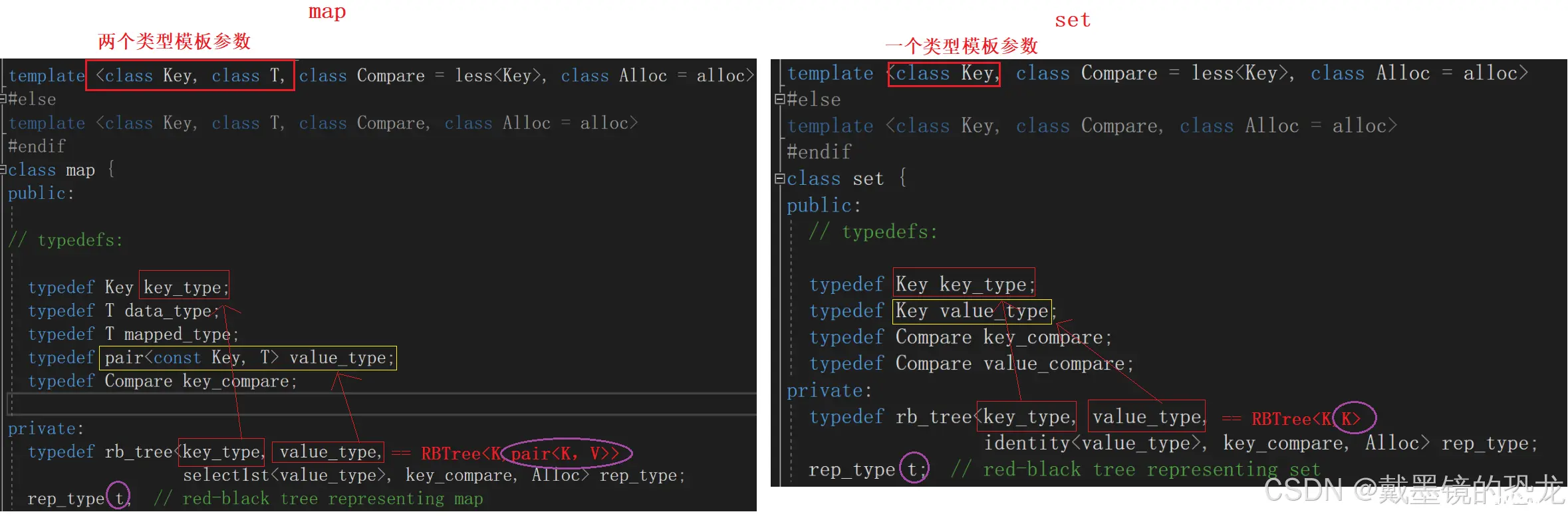
我很疑惑为什么它们两个都传了两个参数给底层的红黑树，那再看一下红黑树的源码

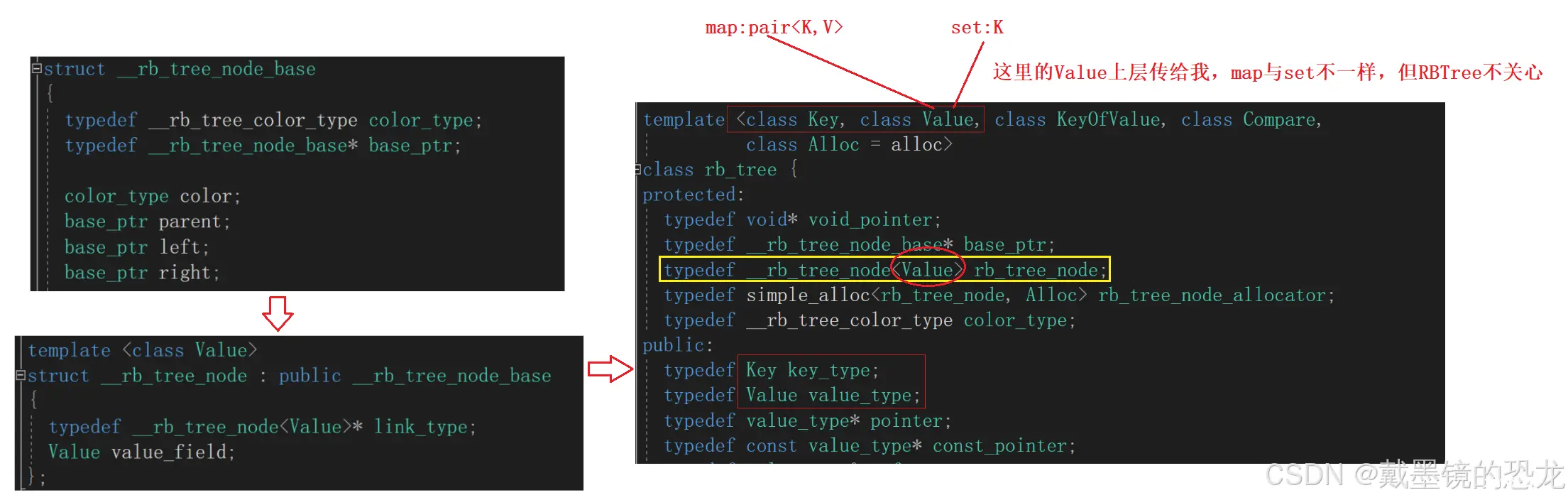
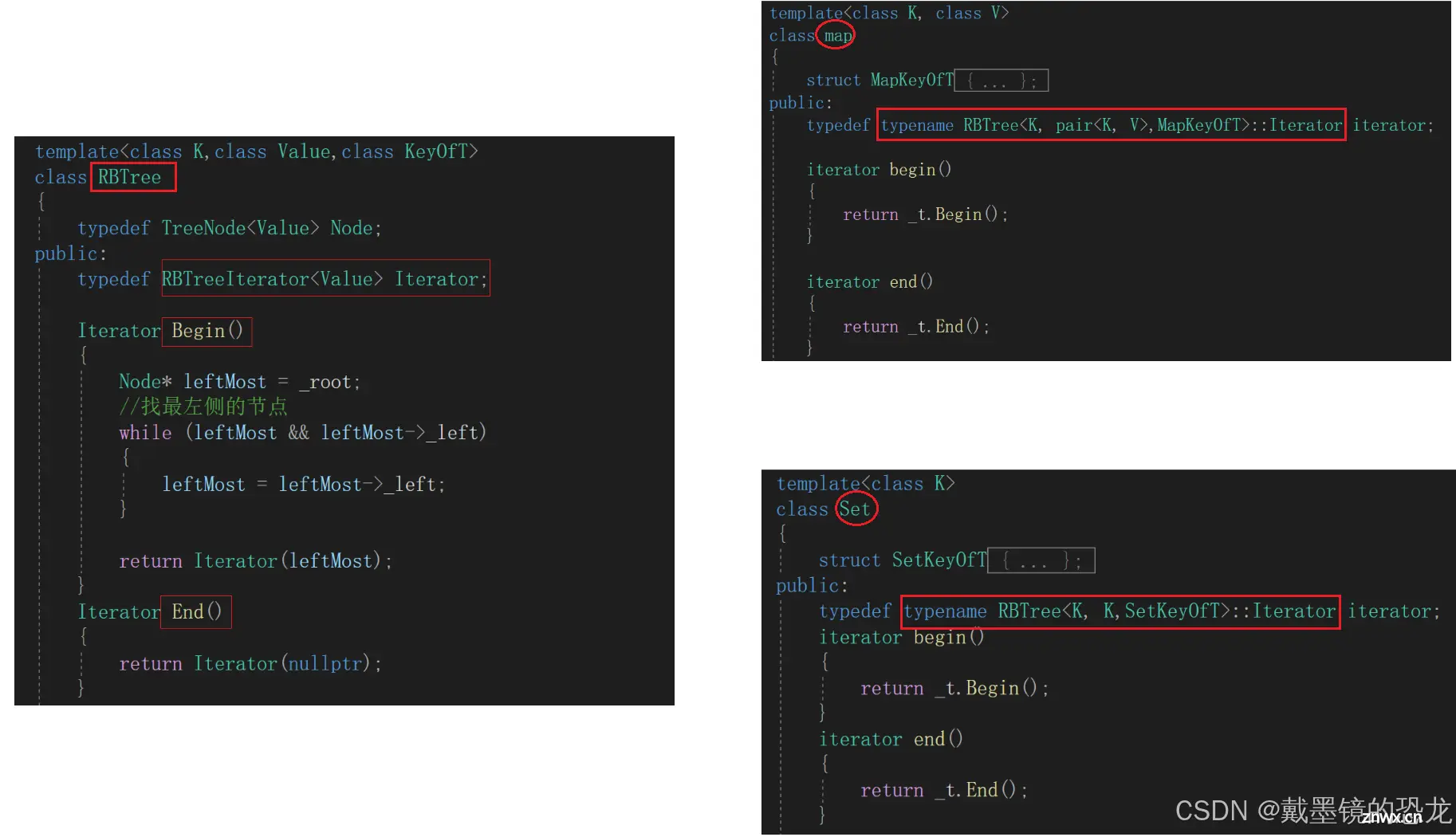
我们可以发现，红黑树在底层不知道你传给它的是什么，为了兼容map与set它搞了两个参数。

但是搞了两个参数后，第一个模板参数Key是不是有点多余呢？

对于set而言，两个K确实是有点多余；对于map来说，pair里面也有K，好像也有点多余如果只留第二个模板参数，_rb_tree_node< Value >，为set时 Value为K；为 map时 Value为pair<K,V>，好像也没问题。对于插入操作，set是k，map是pair还挺好；但是对于查找操作时，set使用Value没问题；map查找时也要使用Value，但map的Value是一个pair(有K，V)，那我既然知道了K和V，我还查找什么呢？所以第一个模板参数不多于，反而是必须

但还有一个问题，在插入操作时，涉及数据比较大小。但是map的Value是一个pair，还得取里面的key；set的Value就是key，此时就比较麻烦。pair默认的比较规则是first比完second比，不符合我们的预期。因此我们还要给红黑树传递一个仿函数，以便获取key。

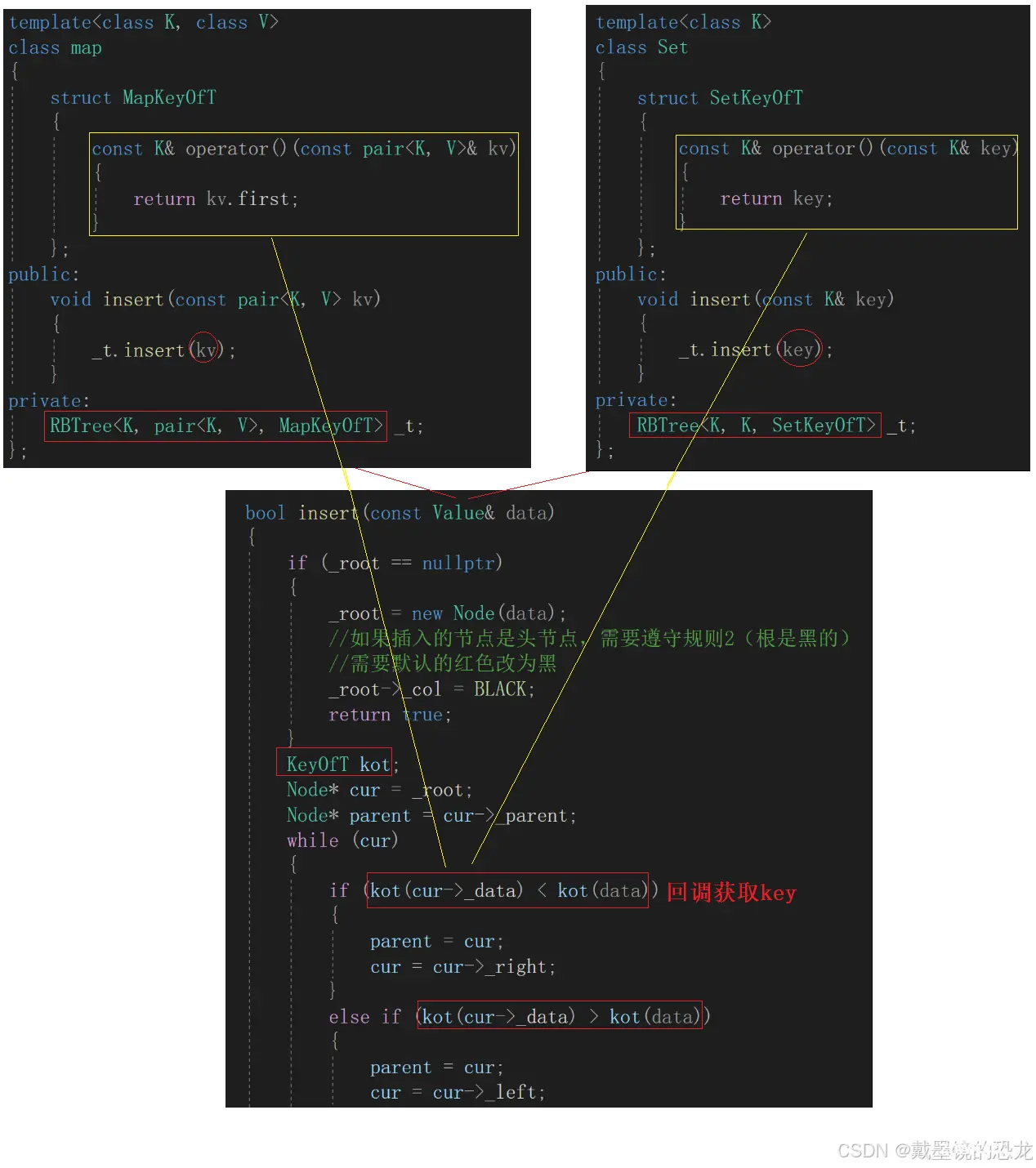
2. 调整红黑树的结构搭建map、set

那我们之前实现的红黑树的结构就得做一下调整了

除了上面呈现出来的模板参数以外，还可以传递自定义的比较规则模板Compare。

下面是map与set的基本框架

原来红黑树中涉及数据比较大小的地方，都得回调传递过来的KeyOfT获取Key后再比较

3. 红黑树的迭代器

3.1 普通迭代器

红黑树的迭代器无非也就是包含一个节点的指针，然后重载指针的各种操作即可。

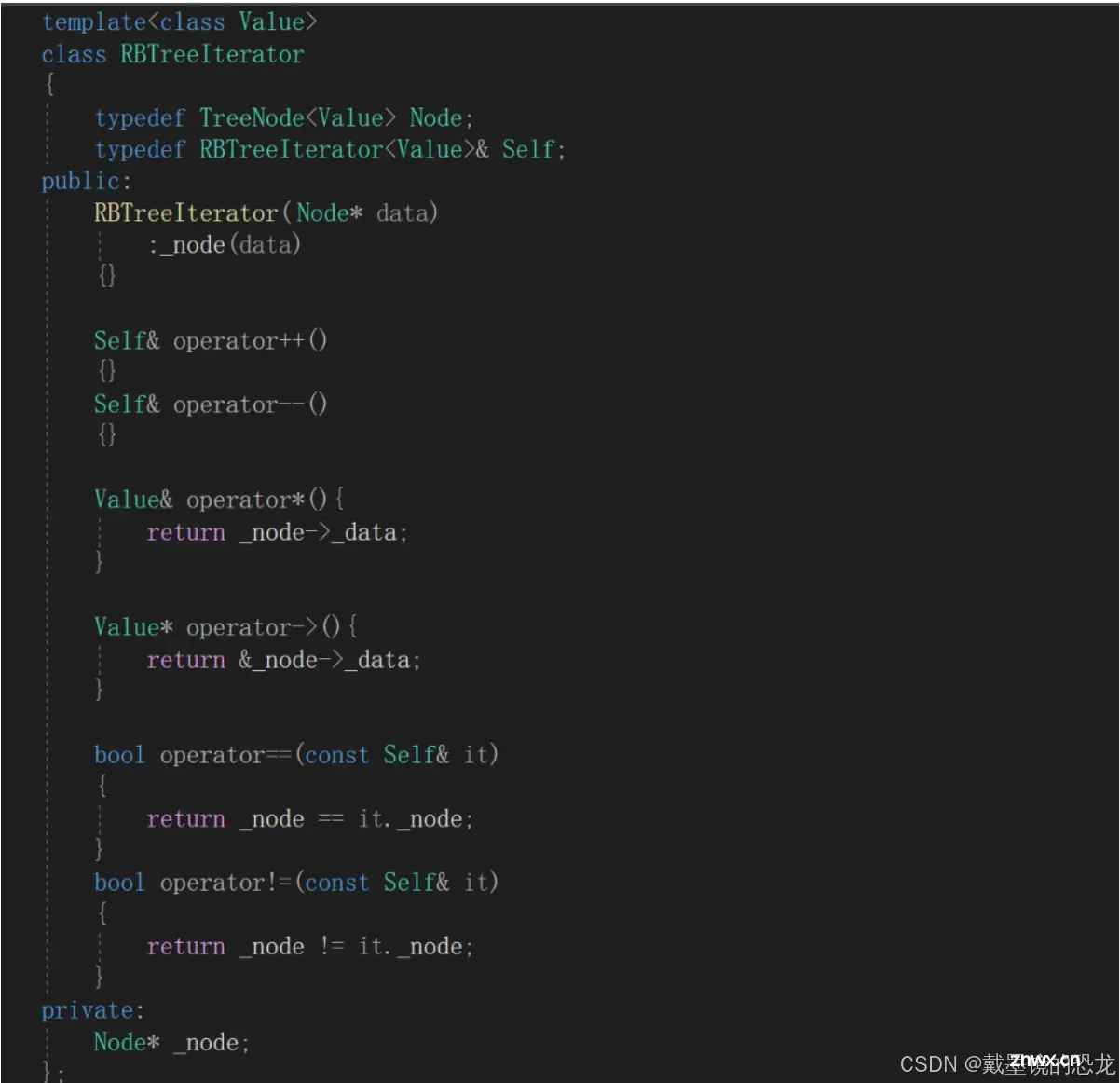
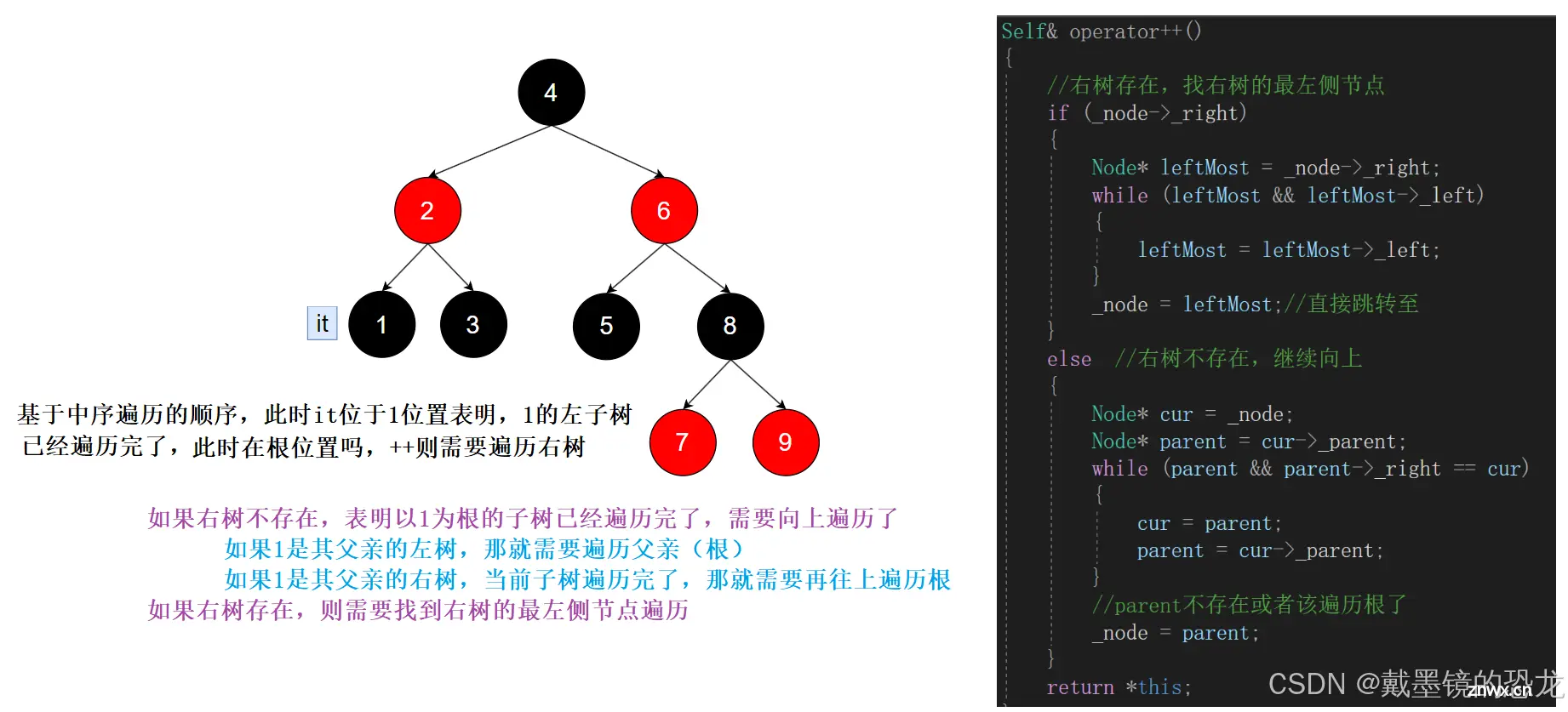
一般迭代器的实现都是按照中序遍历，遍历完是有序的。所以红黑树迭代器的begin()，应该是树最左侧的节点；对于迭代器的end()，我们就按照NULL来处理。

那红黑树迭代器的++与- -操作是如何实现的呢？

对于++操作：

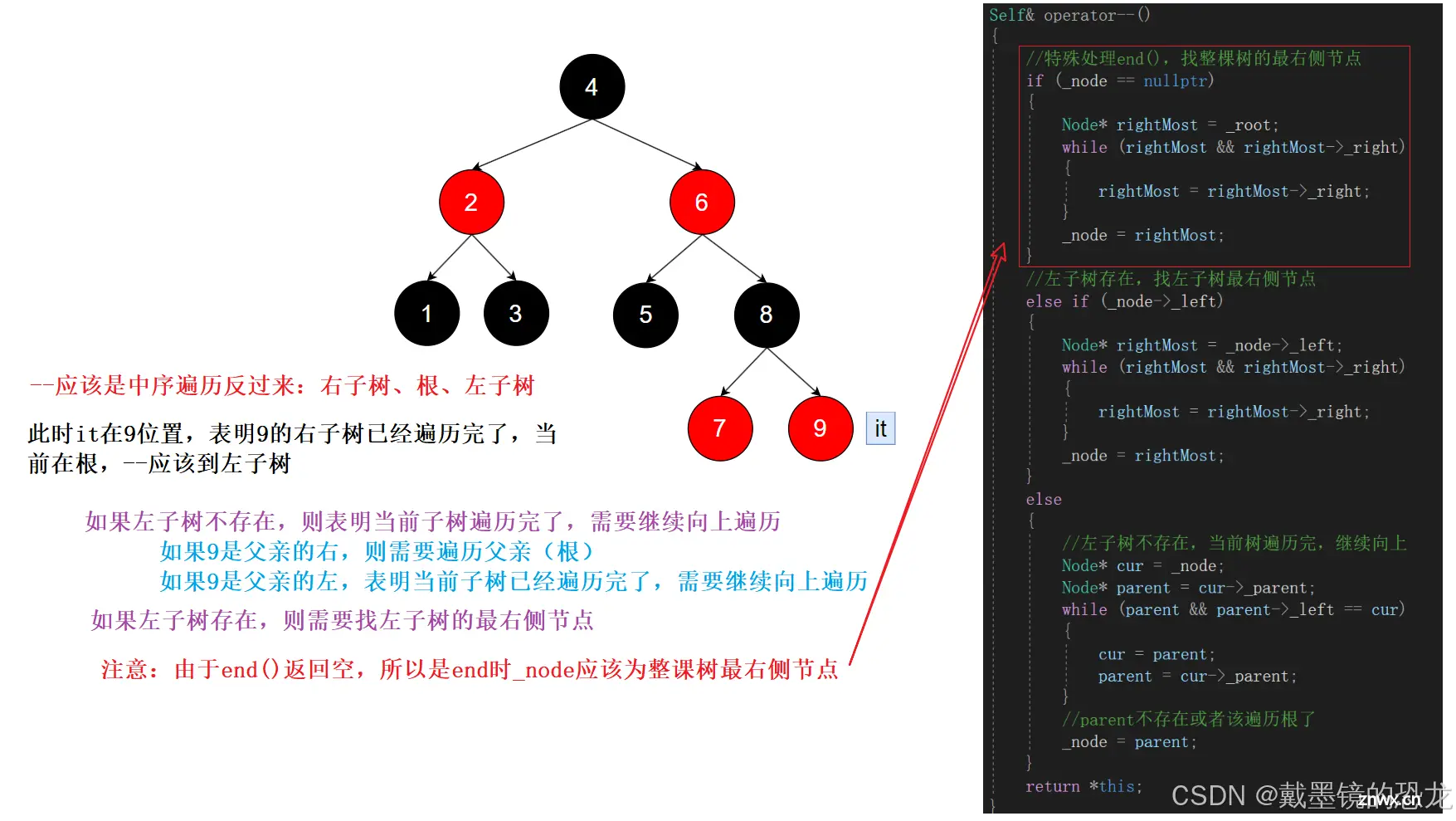
对于- -操作：为了方便_node == nullptr时找树最右侧的节点，我们再给迭代器加一个指针root记录树的根。

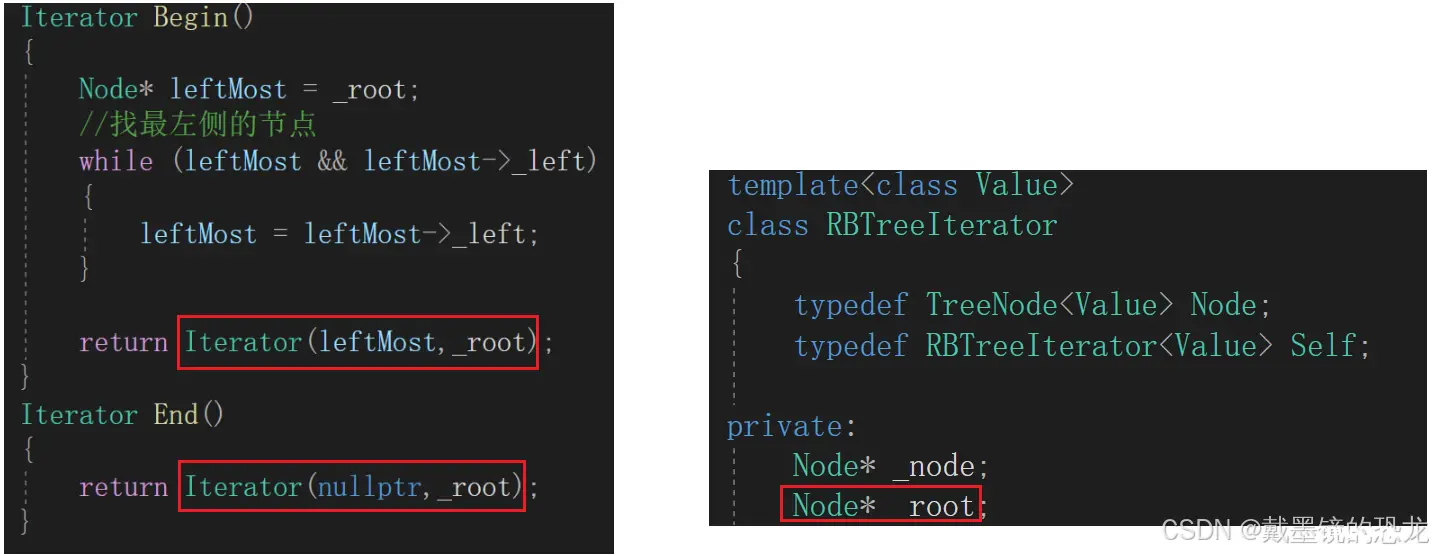
<code>template<class Value>

class RBTreeIterator

{ -- -->

typedef TreeNode<Value> Node;

typedef RBTreeIterator<Value> Self;

private:

Node* _node;

Node* _root;

public:

RBTreeIterator(Node* data,Node* root)

:_node(data)

,_root(root)

{ }

Self& operator++()

{

//右树存在，找右树的最左侧节点

if (_node->_right)

{

Node* leftMost = _node->_right;

while (leftMost && leftMost->_left)

{

leftMost = leftMost->_left;

}

_node = leftMost;//直接跳转至

}

else //右树不存在，继续向上

{

Node* cur = _node;

Node* parent = cur->_parent;

while (parent && parent->_right == cur)

{

cur = parent;

parent = cur->_parent;

}

//parent不存在或者该遍历根了

_node = parent;

}

return *this;

}

Self& operator--()

{

//特殊处理end()，找整棵树的最右侧节点

if (_node == nullptr)

{

Node* rightMost = _root;

while (rightMost && rightMost->_right)

{

rightMost = rightMost->_right;

}

_node = rightMost;

}

//左子树存在，找左子树最右侧节点

else if (_node->_left)

{

Node* rightMost = _node->_left;

while (rightMost && rightMost->_right)

{

rightMost = rightMost->_right;

}

_node = rightMost;

}

else

{

//左子树不存在，当前树遍历完，继续向上

Node* cur = _node;

Node* parent = cur->_parent;

while (parent && parent->_left == cur)

{

cur = parent;

parent = cur->_parent;

}

//parent不存在或者该遍历根了

_node = parent;

}

return *this;

}

Value& operator*(){

return _node->_data;

}

Value* operator->(){

return &_node->_data;

}

bool operator==(const Self& it)

{

return _node == it._node;

}

bool operator!=(const Self& it)

{

return _node != it._node;

}

};

3.2 const迭代器

对于const迭代器而言，无非就是数据不能被修改，那也就是针对迭代器的operator* 与operator->了。

那就先改造底层的迭代器

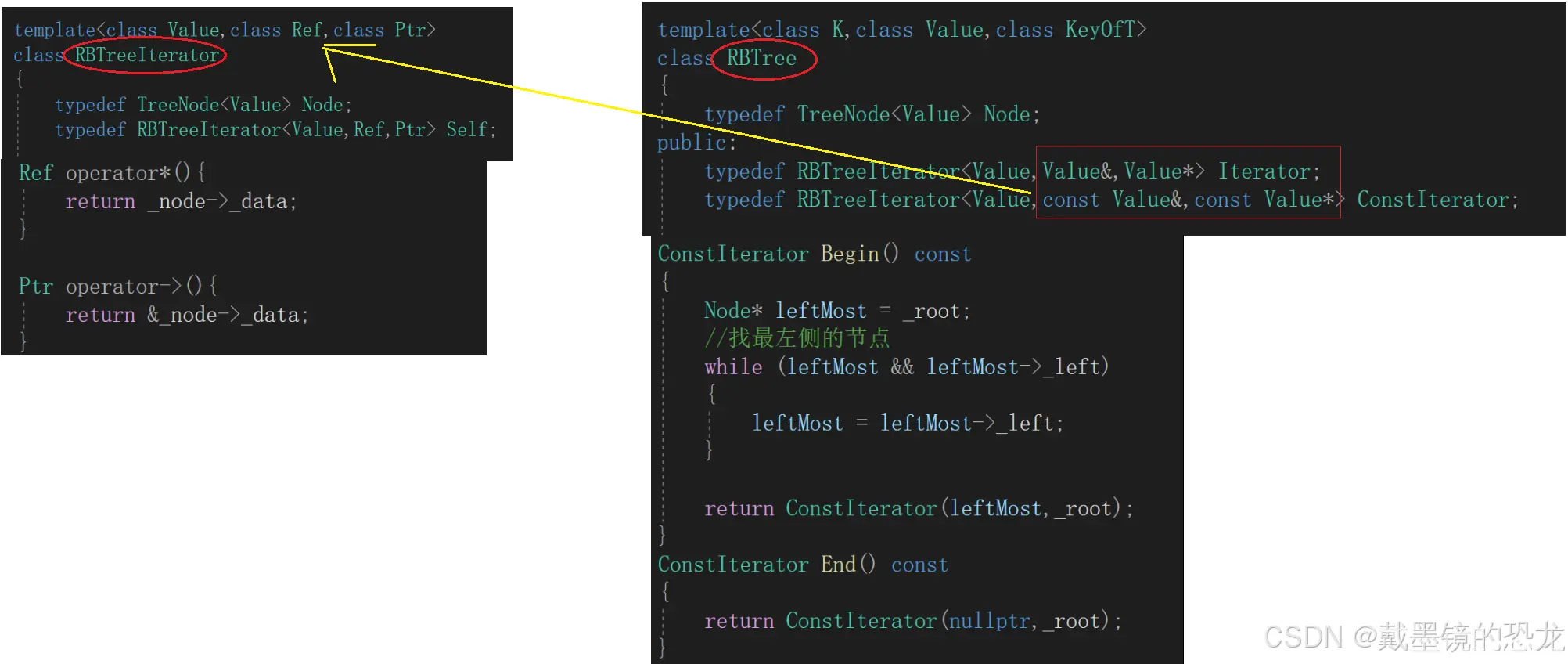
然后map与set在上层封一下就行了

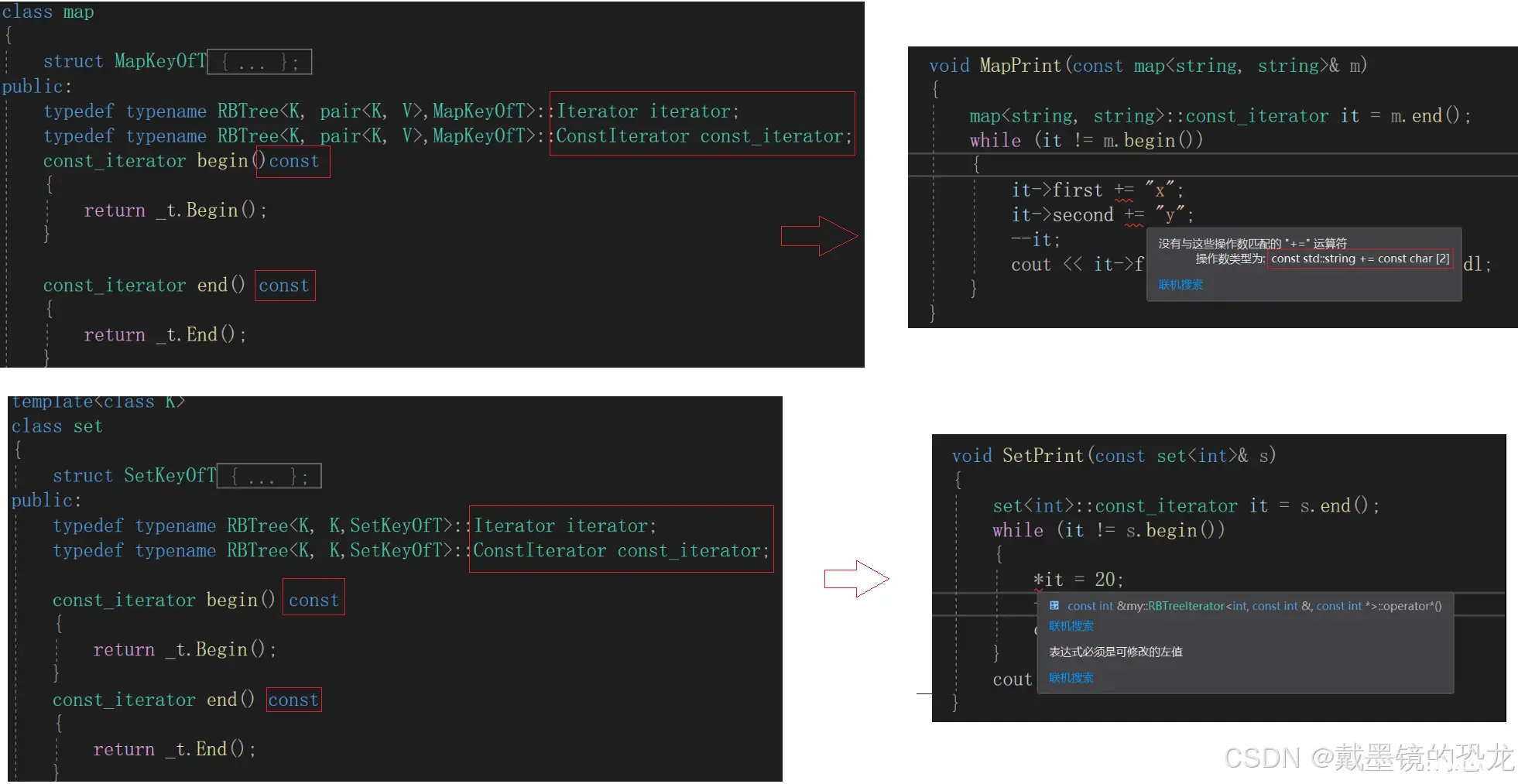
通过上面的我们可以看到，使用const迭代器以后确实都不能修改了；但是普通迭代器存在一个问题：

所以上层在传递给下层时，我们可以将k设置为const

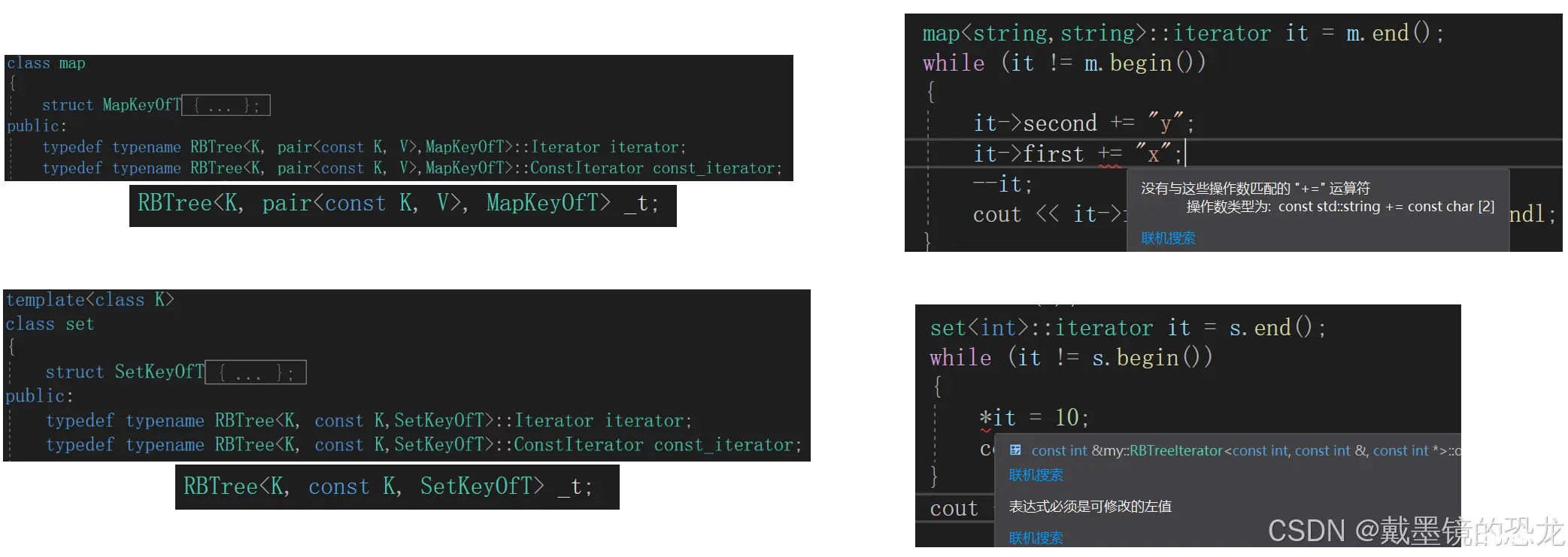
到这里我们的迭代器就完美了。

3.3 map的operator[ ]

我们都知道map重载的[ ]既可以充当插入，也可以充当修改。那么在底层它用的就是insert。（点击可看map的使用）

那我们就需要改变一下insert的返回值了。

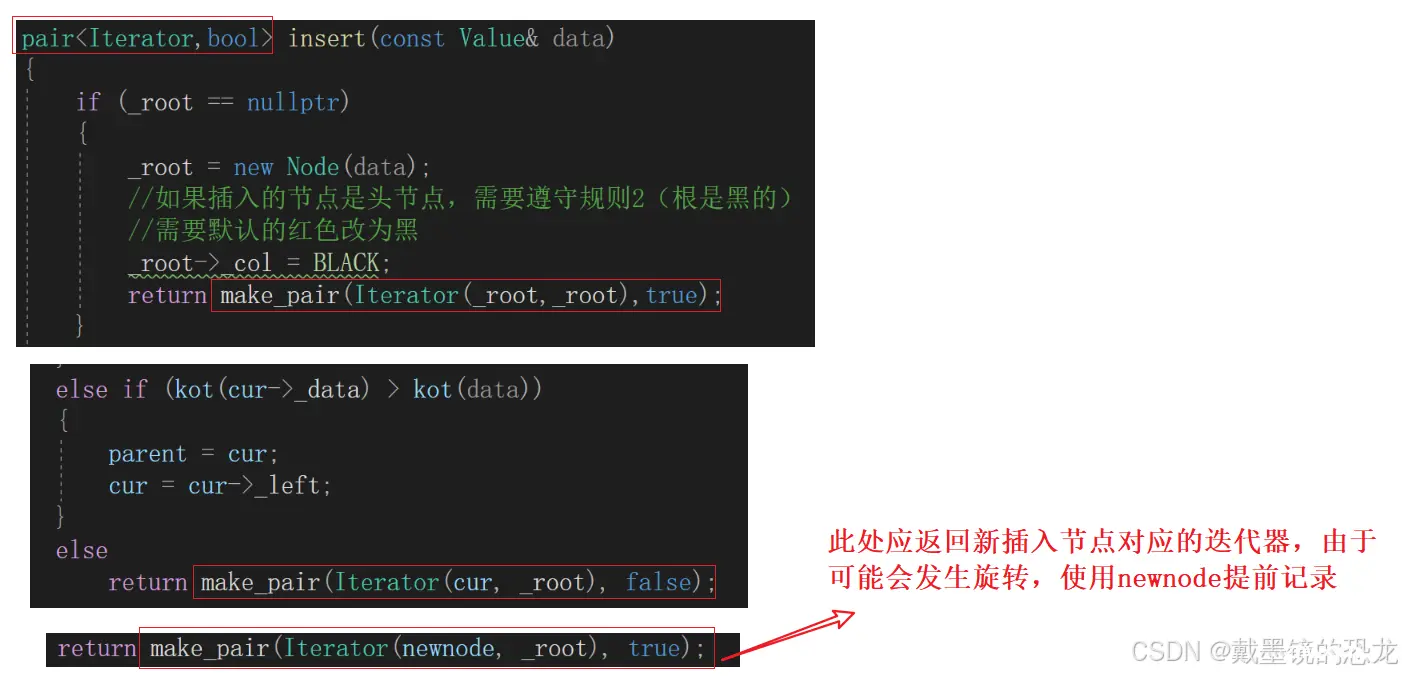
到这里我们map与set的封装就结束了。

4. 完整代码

4.1 RBTree

<code>#pragma once

namespace my

{ -- -->

//颜色

enum Color

{

RED = 0,

BLACK

};

template<class Value>

struct TreeNode

{

Value _data;

TreeNode<Value>* _left;

TreeNode<Value>* _right;

TreeNode<Value>* _parent;//前驱节点

Color _col;

TreeNode(const Value& data)

: _data(data)

, _left(nullptr)

, _right(nullptr)

, _parent(nullptr)

, _col(RED)//默认新节点为红色的

{ }

};

template<class Value,class Ref,class Ptr>

class RBTreeIterator

{

typedef TreeNode<Value> Node;

typedef RBTreeIterator<Value,Ref,Ptr> Self;

private:

Node* _node;

Node* _root;

public:

RBTreeIterator(Node* data,Node* root)

:_node(data)

,_root(root)

{ }

Self& operator++()

{

//右树存在，找右树的最左侧节点

if (_node->_right)

{

Node* leftMost = _node->_right;

while (leftMost && leftMost->_left)

{

leftMost = leftMost->_left;

}

_node = leftMost;//直接跳转至

}

else //右树不存在，继续向上

{

Node* cur = _node;

Node* parent = cur->_parent;

while (parent && parent->_right == cur)

{

cur = parent;

parent = cur->_parent;

}

//parent不存在或者该遍历根了

_node = parent;

}

return *this;

}

Self& operator--()

{

//特殊处理end()，找整棵树的最右侧节点

if (_node == nullptr)

{

Node* rightMost = _root;

while (rightMost && rightMost->_right)

{

rightMost = rightMost->_right;

}

_node = rightMost;

}

//左子树存在，找左子树最右侧节点

else if (_node->_left)

{

Node* rightMost = _node->_left;

while (rightMost && rightMost->_right)

{

rightMost = rightMost->_right;

}

_node = rightMost;

}

else

{

//左子树不存在，当前树遍历完，继续向上

Node* cur = _node;

Node* parent = cur->_parent;

while (parent && parent->_left == cur)

{

cur = parent;

parent = cur->_parent;

}

//parent不存在或者该遍历根了

_node = parent;

}

return *this;

}

Ref operator*(){

return _node->_data;

}

Ptr operator->(){

return &_node->_data;

}

bool operator==(const Self& it)

{

return _node == it._node;

}

bool operator!=(const Self& it)

{

return _node != it._node;

}

};

template<class K,class Value,class KeyOfT>

class RBTree

{

typedef TreeNode<Value> Node;

public:

typedef RBTreeIterator<Value,Value&,Value*> Iterator;

typedef RBTreeIterator<Value,const Value&,const Value*> ConstIterator;

Iterator Begin()

{

Node* leftMost = _root;

//找最左侧的节点

while (leftMost && leftMost->_left)

{

leftMost = leftMost->_left;

}

return Iterator(leftMost,_root);

}

Iterator End()

{

return Iterator(nullptr,_root);

}

ConstIterator Begin() const

{

Node* leftMost = _root;

//找最左侧的节点

while (leftMost && leftMost->_left)

{

leftMost = leftMost->_left;

}

return ConstIterator(leftMost,_root);

}

ConstIterator End() const

{

return ConstIterator(nullptr,_root);

}

RBTree() = default;

RBTree(const RBTree<K, Value,KeyOfT>& tree)

{

this->_root = Copy(tree._root);

}

//类里面直接写类名，无需传递模板参数也可。

RBTree& operator=(RBTree tree)

{

swap(this->_root, tree._root);//现代写法

return *this;

}

~RBTree()

{

Destroy(_root);

}

pair<Iterator,bool> insert(const Value& data)

{

if (_root == nullptr)

{

_root = new Node(data);

//如果插入的节点是头节点，需要遵守规则2（根是黑的）

//需要默认的红色改为黑

_root->_col = BLACK;

return make_pair(Iterator(_root,_root),true);

}

KeyOfT kot;

Node* cur = _root;

Node* parent = cur->_parent;

while (cur)

{

if (kot(cur->_data) < kot(data))

{

parent = cur;

cur = cur->_right;

}

else if (kot(cur->_data) > kot(data))

{

parent = cur;

cur = cur->_left;

}

else

return make_pair(Iterator(cur, _root), false);

}

//孩子连父亲

cur = new Node(data);

Node* newnode = cur;

cur->_parent = parent;

//父亲连孩子

if (kot(parent->_data) < kot(data))

parent->_right = cur;

else

parent->_left = cur;

//检查是否违反红黑树的规则

//如果父亲存在且为红，则违反规则

while (parent && parent->_col == RED)

{

Node* grandfather = parent->_parent;

if (grandfather->_left == parent)

{

//根据爷爷节点找叔叔

Node* uncle = grandfather->_right;

//如果叔叔存在且为红,仅需要变色

if (uncle && uncle->_col == RED)

{

parent->_col = BLACK;

uncle->_col = BLACK;

grandfather->_col = RED;

//然后继续向上调整

cur = grandfather;

parent = cur->_parent;

}

//如果叔叔不存在 或者存在且为黑，需要旋转+变色

else

{

//判断单旋(直树)还是双旋(弯树)

//单旋

if (parent->_left == cur)

{

// g

// p u

//c

RotateR(grandfather);

parent->_col = BLACK;

grandfather->_col = RED;

}

//双旋

else

{

// g

// p u

// c

RotateL(parent);

RotateR(grandfather);

cur->_col = BLACK;

grandfather->_col = RED;

}

break;//旋转后已经符合规则，无需再调整了

}

}

//grandfather->_right == parent

else

{

Node* uncle = grandfather->_left;

//如果叔叔存在且为红,仅需要变色

if (uncle && uncle->_col == RED)

{

parent->_col = BLACK;

uncle->_col = BLACK;

grandfather->_col = RED;

//继续调整

cur = grandfather;

parent = cur->_parent;

}

//如果叔叔不存在 或者存在且为黑，需要旋转+变色

else

{

// g

// u p

// c

if (parent->_right == cur)

{

RotateL(grandfather);

parent->_col = BLACK;

grandfather->_col = RED;

}

// g

// u p

// c

else

{

RotateR(parent);

RotateL(grandfather);

cur->_col = BLACK;

grandfather->_col = RED;

}

break;

}

}

}

//父亲不存在，或者父亲为黑时，无需判断，直接将根变黑

_root->_col = BLACK;

return make_pair(Iterator(newnode, _root), true);

}

Iterator* find(const K& key)

{

Node* cur = _root;

KeyOfT kot;

while (cur)

{

if ( kot(cur->_data)< key)

cur = cur->_right;

else if (kot(cur->_data) > key)

cur = cur->_left;

else

return Iterator(cur,_root);

}

return End();

}

void InOrder()

{

_InOrder(_root);

cout << endl;

}

bool IsRBTree()

{

Node* root = _root;

if (root == nullptr)//空树也是

return true;

if (root->_col == RED)

{

cout << "根节点为红色，违反规则" << endl;

return false;

}

//先统计最左侧路径上有多少黑节点作为标准

Node* cur = root;

int blackNum = 0;

while (cur)

{

if (cur->_col == BLACK)

blackNum++;

cur = cur->_left;

}

//k用来记录路径中黑节点的个数

int k = 0;

//在依据标准黑节点的个数，比较其它路径

return _IsRBTree(root, blackNum, k);

}

int Size()

{

return _Size(_root);

}

int Height()

{

return _Height(_root);

}

private:

int _Height(Node* root)

{

if (root == nullptr)

return 0;

int leftH = _Height(root->_left);

int rightH = _Height(root->_right);

return leftH > rightH ? leftH + 1 : rightH + 1;

}

int _Size(Node* root)

{

if (root == nullptr)

return 0;

return 1 + _Size(root->_left) + _Size(root->_right);

}

bool _IsRBTree(Node* root, int blackNum, int k)

{

//一条路径走完，比较黑节点的个数

if (root == nullptr)

{

if (blackNum != k)

{

cout << "路径黑节点个数不相等，违反规则" << endl;

return false;

}

return true;

}

Node* parent = root->_parent;

if (parent && root->_col == RED && parent->_col == RED)

{

cout << "存在连续的红节点，违反规则" << endl;

return false;

}

//统计黑节点

if (root->_col == BLACK)

k++;

//统计完根，在依次统计左右子树

return _IsRBTree(root->_left, blackNum, k)

&& _IsRBTree(root->_right, blackNum, k);

}

void RotateR(Node* parent)

{

Node* SubL = parent->_left;

Node* SubLR = SubL->_right;

//降级连兵

parent->_left = SubLR;

if (SubLR)

SubLR->_parent = parent;

Node* parentParent = parent->_parent;

//升级连将

SubL->_right = parent;

parent->_parent = SubL;

//将连将

SubL->_parent = parentParent;

if (parentParent == nullptr)

{

_root = SubL;

}

else

{

if (parentParent->_left == parent)

parentParent->_left = SubL;

else

parentParent->_right = SubL;

}

}

void RotateL(Node* parent)

{

Node* SubR = parent->_right;

Node* SubRL = SubR->_left;

//降级连兵

parent->_right = SubRL;

if (SubRL)

SubRL->_parent = parent;

Node* parentParent = parent->_parent;

//升级连将

SubR->_left = parent;

parent->_parent = SubR;

//将连将

SubR->_parent = parentParent;

if (parentParent == nullptr)

_root = SubR;

else

{

if (parentParent->_left == parent)

parentParent->_left = SubR;

else

parentParent->_right = SubR;

}

}

void Destroy(Node* root)

{

if (root == nullptr)

return;

Destroy(root->_left);

Destroy(root->_right);

delete root;

}

Node* Copy(Node* root)

{

if (root == nullptr)

return nullptr;

_root->_left = Copy(root->_left);

_root->_right = Copy(root->_right);

return _root;

}

void _InOrder(Node* root)

{

if (root == nullptr)

return;

_InOrder(root->_left);

cout << root->_kv.first << " ";

_InOrder(root->_right);

}

Node* _root;

};

}

4.2 MyMap

#pragma once

#include"RBTree.h"

namespace my

{

template<class K, class V>

class map

{

struct MapKeyOfT

{

const K& operator()(const pair<K, V>& kv)

{

return kv.first;

}

};

public:

typedef typename RBTree<K, pair<const K, V>,MapKeyOfT>::Iterator iterator;

typedef typename RBTree<K, pair<const K, V>,MapKeyOfT>::ConstIterator const_iterator;

const_iterator begin()const

{

return _t.Begin();

}

const_iterator end() const

{

return _t.End();

}

iterator begin()

{

return _t.Begin();

}

iterator end()

{

return _t.End();

}

pair<iterator, bool> insert(const pair<K, V> kv)

{

return _t.insert(kv);

}

bool find(const K& key)

{

return _t.find(key);

}

V& operator[](const K& key)

{

pair<iterator, bool> ret = insert(make_pair(key,V()));

//如果key存在，则返回其对应的value

//如果key不存在，则插入它，其value为类型的默认值

return ret.first->second;

}

private:

RBTree<K, pair<const K, V>, MapKeyOfT> _t;

};

//void MapPrint(const map<string, string>& m)

//{

//map<string, string>::const_iterator it = m.end();

//while (it != m.begin())

//{

//it->first += "x";

//it->second += "y";

//--it;

//cout << it->first << " " << it->second << endl;

//}

//}

void testmap()

{

map<string, string> m;

m.insert({ "right","右"});

m.insert({ "up","上"});

m.insert({ "down","下"});

m.insert({ "left","左"});

m["left"] = "修改左";

m["offer"] = "新增";

//cout << m.find(3) << endl;

//for (auto& e : m)

//{

//cout << e.first << " " << e.second << endl;

//}

//MapPrint(m);

map<string,string>::iterator it = m.end();

while (it != m.begin())

{

//it->second += "y";

//it->first += "x";

--it;

cout << it->first << " " << it->second << endl;

}

cout << endl;

}

}

4.3 MySet

#pragma once

#include"RBTree.h"

namespace my

{

template<class K>

class set

{

struct SetKeyOfT

{

const K& operator()(const K& key)

{

return key;

}

};

public:

typedef typename RBTree<K, const K,SetKeyOfT>::Iterator iterator;

typedef typename RBTree<K, const K,SetKeyOfT>::ConstIterator const_iterator;

const_iterator begin() const

{

return _t.Begin();

}

const_iterator end() const

{

return _t.End();

}

iterator begin()

{

return _t.Begin();

}

iterator end()

{

return _t.End();

}

pair<iterator, bool> insert(const K& key)

{

return _t.insert(key);

}

bool find(const K& key)

{

return _t.find(key);

}

private:

RBTree<K, const K, SetKeyOfT> _t;

};

//void SetPrint(const set<int>& s)

//{

//set<int>::const_iterator it = s.end();

//while (it != s.begin())

//{

////*it = 20;

//--it;

//cout << *it << " ";

//}

//cout << endl;

//}

void testset()

{

set<int> s;

pair<set<int>::iterator,bool> ret = s.insert(5);

cout << *(ret.first) << endl;//查看insert的返回值

s.insert(2);

s.insert(8);

s.insert(15);

s.insert(2);

s.insert(9);

set<int>::iterator it = s.end();

while (it != s.begin())

{

//*it = 10;

--it;

cout << *it <<" ";

}

cout << endl;

//SetPrint(s);

}

}