定义

堆是一棵完全二叉树。分为大顶堆和小顶堆

大顶推：所有节点都大于等于它的两个子节点

小顶堆：所有节点都小于等于它的两个子节点

伪代码

推排序步骤，以升序排列为例，用大顶堆。（降序排列，用小顶堆）

1. 构建大顶推
2. 把堆顶元素和堆尾元素交换，此时堆尾元素是最大的，堆的大小减一
3. 堆顶元素下沉到指定位置
4. 重复2-3步，直到堆的大小为1

关键在于如何构建一个大顶堆（对节点进行下沉）:

从最后一个非叶子节点开始；

逐个检查每个节点，如果一个节点的值小于其子节点的值，我们就将它与较大的子节点交换位置；

交换后，这个交换后的节点可能导致不满足堆的特性，因此还需要继续下沉（Heapify)

举个例子

需要注意的是：对于一个完全二叉树

它的最后一个非叶节点下标是 <code>Math.floor(len/2) - 1,len是二叉树的节点个数

下标为i的节点，它的左子节点是2*i+1, 右子节点是2*i+2

比如说对于[5,2,7,3,6,1,4]

最后一个非叶子节点下标是Math.floor(len/2) - 1=2, 也就是说最后一个非叶子节点是7, 构建最大堆的过程如下：

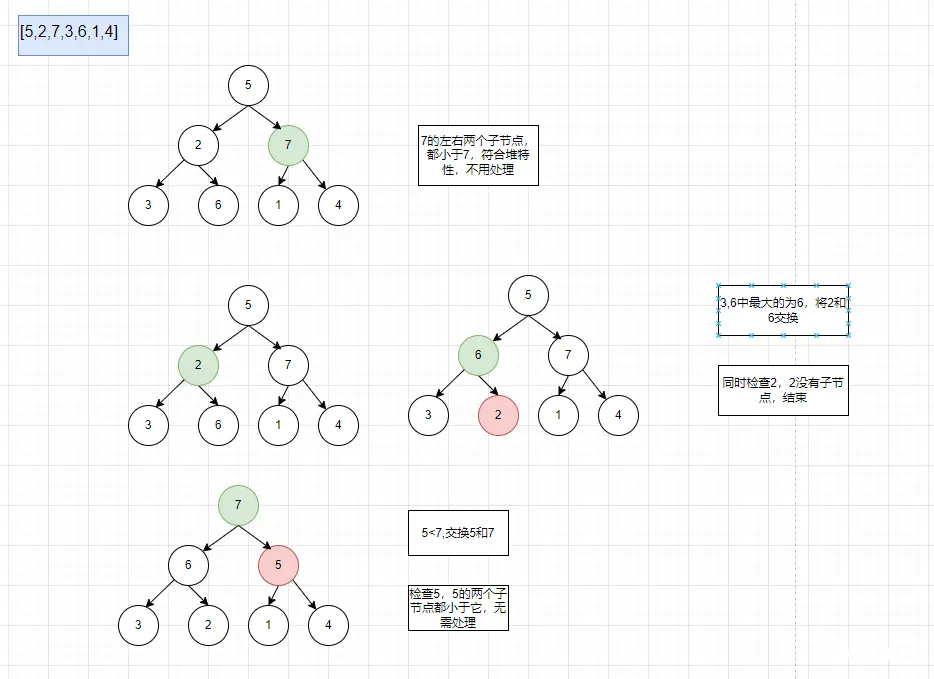
时间复杂度

O(nlogn)

实现

<code>function heapSort(arr) {

// 构建最大堆

let n = arr.length;

for(let i = Math.floor(n/2 - 1); i>=0;i--) {

heapify(arr, n, i) // 把下标为i的节点放到合适的位置上

}

while(n>1) {

// 交换堆顶元素和堆尾元素

[arr[0], arr[n-1]] = [arr[n-1], arr[0]]

// 堆的个数减一

n--

// 把堆顶元素放到合适的位置

heapify(arr, n, 0)

}

}

function heapify(arr, n, i) {

let largestIndex = i

let leftIndex = 2 * i + 1

let rightIndex = 2 * i + 2

if(leftIndex < n && arr[leftIndex] > arr[largestIndex]) {

largestIndex = leftIndex

}

if(rightIndex < n && arr[rightIndex] > arr[largestIndex]) {

largestIndex = rightIndex

}

if(largestIndex!==i) {

[arr[i], arr[largestIndex]] = [arr[largestIndex], arr[i]]

heapify(arr, n, largestIndex)

}

}