文章目录

一、Matlab 是什么？1.1Matlab工作环境1.1Matlab常用命令1.1Matlab快捷键

二、Matlab计算介绍2.1数值计算

三、matlab中size()函数的用法四、MATLAB中ones()函数的用法五、矩阵相乘和矩阵点乘六、matlab之将控制权给予键盘函数keyboard6.1功能6.2语法6.3示例

七、MatLab中linspace作用7.1函数简介7.2应用举例

八、Matlab基本函数-length函数九、matlab中axis square与axis equal区别十、【MATLAB】进阶绘图 ( Pie Chart 饼图 | pie 函数 | 三维饼图 | pie3 函数 )10.1pie 函数10.2pie3 函数10.3饼图示例

十一、matlab中ut=[t,ones(size(t))]十二、用于专门学科的特殊矩阵12.1魔方矩阵(方阵、magic函数)12.2范德蒙矩阵(方阵、vander函数)12.3希尔伯特矩阵(方阵、hilb函数)12.4伴随矩阵(方阵、compan函数)12.5帕斯卡矩阵(方阵、pascal函数)

十三、MATLAB中：冒号用法13.1 x(:, :, : )13.2 x(1, : )13.3 x(:, : )

十四、matlab中的findstr与strfind函数14.1 findstr(s1,s2)14.2 strfind(s1,s2)

十五、Matlab rand（）函数用法十六、MATLAB中squeeze函数的作用十七、Matlab之魔方阵magic十八、Matlab的concur、repmat、kron、reshape函数介绍18.1 concur18.2 repmat函数18.3 kron函数18.4 reshape18.5补充：矩阵向量化

十九、Matlab之logspace二十、matlab的format指令二十一、matlab 中disp()常见用法二十二、Matlab mapminmax函数使用及原理二十三、matlab 中num2str函数的使用二十四、matlab遗传算法gatbx工具箱介绍及安装说明二十五、matlab的svm算法调试总结

---

一、Matlab 是什么？

MATLAB是矩阵实验室（Matrix Laboratory）之意。是由美国mathworks公司发布的主要面对科学计算、可视化以及交互式程序设计的高科技计算环境。

现在的Matlab要包括MATLAB和Simulink两大部分。

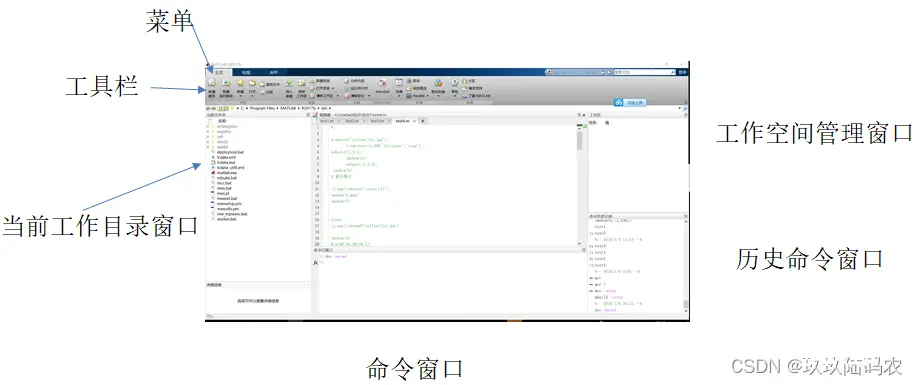
1.1Matlab工作环境

1.1Matlab常用命令

1.1Matlab快捷键

二、Matlab计算介绍

2.1数值计算

MATLAB的数值计算 —— matlab 具有出色的数值计算能力，占据世界上数值计算软件的主导地位

数值运算的功能

创建矩阵矩阵运算多项式运算线性方程组数值统计线性插值函数优化微分方程的数值解

三、matlab中size()函数的用法

size（）：获取矩阵的行数和列数

（1）s=size(A),

<code> 当只有一个输出参数时，返回一个行向量，该行向量的第一个元素时矩阵的行数，第二个元素是矩阵的列数。

（2）[r,c]=size(A),

当有两个输出参数时，size函数将矩阵的行数返回到第一个输出变量r，将矩阵的列数返回到第二个输出变量c。

（3）size(A,n)如果在size函数的输入参数中再添加一项n，并用1或2为n赋值，则 size将返回矩阵的行数或列数。其中r=size(A,1)该语句返回的时矩阵A的行数， c=size(A,2) 该语句返回的时矩阵A的列数。

另外，length()=max(size()).

四、MATLAB中ones()函数的用法

ones 创建全部为 1 的数组

语法：

X = ones

X = ones(n)

X = ones(sz1,…,szN)

X = ones(sz)

X = ones(___,typename)

X = ones(___,‘like’,p)

注解：

X = ones 返回标量 1。

X = ones(n) 返回一个 n×n 的全 1 矩阵。

X = ones(sz1,…,szN) 返回由 1 组成的 sz1×…×szN 数组，其中 sz1,…,szN 指示每个维度的大小。例如，ones(2,3,4) 返回由 1 组成的 2×3 ×4数组。

X = ones(sz) 返回一个由 1 组成的数组，其中大小向量 sz 定义 size(X)。例如，ones([2,3]) 返回由 1 组成的 2×3 数组。

X = ones(___,typename) 在上述语法的基础上进一步指定 X 的数据类型（类）。例如，ones(5,‘int8’) 返回 8 位整数组成的 5×5 矩阵。

X = ones(___,‘like’,p) 指定 X 具有与数值变量 p 相同的数据类型、稀疏性和复/实性（实数或复数）。

其中参数：

n - 方阵的大小 整数值

sz - 输出大小 由整数值组成的行向量

typename - 输出类 ‘double’ （默认） | ‘single’ | ‘logical’ | ‘int8’ | ‘uint8’ | …

p - 原型 变量

五、矩阵相乘和矩阵点乘

矩阵相乘也就是矩阵的乘法操作要求左矩阵的列和右矩阵的行数要一致起来

A=[1 1 1;2 2 2] B=[3 3;4 4;5 5;]

MATLAB 语句：A*B

矩阵的点乘则要求矩阵必须维数相等，即MxN维矩阵乘以MxN维矩阵

A=[1 1 1;2 2 2] B=[3 3 3;4 4 4]

MATLAB语句：A.*B

各元素逐一相乘，A和B可以调换顺序。

六、matlab之将控制权给予键盘函数keyboard

6.1功能

将控制权给予键盘

6.2语法

keyboard 暂停执行正在运行的程序，并将控制权交给键盘。

将 keyboard 函数放入程序中您希望 MATLAB® 暂停的位置。

当程序暂停时，命令行窗口中的提示符将更改为 K>>，指示 MATLAB 处于调试模式。

然后查看或更改变量的值，以查看新值是否产生预期的结果。

keyboard 函数对调试函数很有用。

6.3示例

使用 keyboard 命令暂停执行程序，并在继续之前修改变量。

创建文件 buggy.m，其中包含以下语句。

function z = buggy(x)

n = length(x);

keyboard

z = (1:n)./x;

运行 buggy.m。MATLAB 将在第 3 行（keyboard 命令所在的位置）暂停。

buggy(5)

将变量 x 乘以 2 并继续运行程序。MATLAB 将使用新的 x 值执行程序的其余部分。

x = x * 2

dbcont

要终止调试模式并继续执行，请使用 dbcont 命令。

要终止调试模式并退出文件而不完成执行，请使用 dbquit 命令。

七、MatLab中linspace作用

linspace是Matlab中的均分计算指令，用于产生x1,x2之间的N点行线性的矢量。

7.1函数简介

用法：linspace(x1,x2,N)

功能：linspace是Matlab中的均分计算指令，用于产生x1,x2之间的N点行线性的矢量。其中x1、x2、N分别为起始值、终止值、元素个数。若默认N，默认点数为100。

在matlab的命令窗口下输入help linspace或者doc linspace可以获得该函数的帮助信息。

相关函数： logspace

用法：x=logspace(a, b, n)

功能：logspace(a, b, n)生成一个(1xn)数组，数据的第一个元素值为a，最后一个元素为b，n是总采样点数。需要注意的是，此时产生的数组元素在10^a 到10^b上并不是均匀分布的，而形成一个对数曲线。

7.2应用举例

例一：

在matlab的命令窗口输入：X=linspace(1,100)

将产生从1到100步长为1的 数组。类似于在命令窗口中输入：

X=[1:1:100]

例二：

在命令窗口中输入：

X=linspace(5,100,20)

将输出：

X =

5 10 15 20 25 30 35 40 45 50 55 60 65 70 75 80 85 90 95 100

这和X=[5:5:100]的效果是一样的。

linspace是Matlab中的均分计算指令，用于产生x1,x2之间的N点行线性的矢量。

八、Matlab基本函数-length函数

1、length函数：计算向量或矩阵的长度

2、用法说明

y = length(x) 函数计算指定向量或矩阵的长度y。如果参数变量x是向量，则返回其长度；如果参数变量是非空矩阵，则length(x)与max(size(x))等价

3、举例说明

>> x = 'youhaidong'

x =

youhaidong

>> y = length(x)

y =

10

>> x = rand(6,6)

x =

0.8147 0.2785 0.9572 0.7922 0.6787 0.7060

0.9058 0.5469 0.4854 0.9595 0.7577 0.0318

0.1270 0.9575 0.8003 0.6557 0.7431 0.2769

0.9134 0.9649 0.1419 0.0357 0.3922 0.0462

0.6324 0.1576 0.4218 0.8491 0.6555 0.0971

0.0975 0.9706 0.9157 0.9340 0.1712 0.8235

>> y = length(x)

y =

6

九、matlab中axis square与axis equal区别

axis square 当前坐标系图形设置为方形

axis equal 将横轴纵轴的定标系数设成相同值 ,即单位长度相同，

也就是说axis square刻度范围不一定一样，但是一定是方形的。

axis equal刻度是等长的，但也不一定是方形的。

用两个简单例子，解释一下

【1】首先是axis square

x=1:0.1:10;

y=x;

plot(y);

axis square;

程序运行结果为，可以发现，该图横纵坐标的刻度范围不同，单位刻度不同，一个是1一个是20，但是整体是一个方形

【2】而axis equal

figure;

x=1:0.1:10;

y=x;

plot(y);

axis equal;

结果为，可以发现，横纵坐标的单位刻度是相同的，都是10，但整体并不是方形

十、【MATLAB】进阶绘图 ( Pie Chart 饼图 | pie 函数 | 三维饼图 | pie3 函数 )

10.1pie 函数

pie 函数 , 传入一个向量作为参数 , 即可在饼图中绘制对应元素的值 , 绘制时根据数值自动分配百分比 ;

% 饼图的数值列表

x = [1, 2, 5, 4, 8];

% 绘制饼图 , 绘制时根据数值自动分配百分比

pie(x);

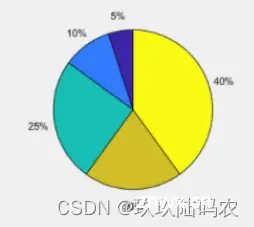
饼图还可以拆分部分扇形独立出来 , 效果如下 ;

使用向量表示哪些部分独立出来 , [ 0 , 0 , 1 , 0 , 1 ] [0, 0, 1, 0, 1][0,0,1,0,1] , 1 11 表示独立出来 , 0 00 表示默认 ;

<code>% 饼图的数值列表

x = [1, 2, 5, 4, 8];

% 绘制饼图 , 绘制时根据数值自动分配百分比

% 后面跟着 有 x 相同个数的向量 ,

% 0 元素代表默认

% 1 元素代表分离出来

pie(x, [0, 0, 1, 0, 1]);

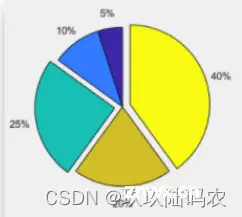
10.2pie3 函数

pie3 函数与 pie 函数用法相同 , 只是绘制的是三维饼图 ;

<code>% 饼图的数值列表

x = [1, 2, 5, 4, 8];

% 绘制 3D 饼图 , 绘制时根据数值自动分配百分比

% 后面跟着 有 x 相同个数的向量 ,

% 0 元素代表默认

% 1 元素代表分离出来

pie3(x, [0, 0, 1, 0, 1]);

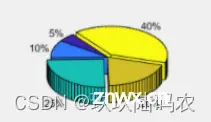
10.3饼图示例

代码示例 :

<code>% 饼图的数值列表

x = [1, 2, 5, 4, 8];

% 绘制第一张图像

subplot(1, 3, 1);

% 绘制饼图 , 绘制时根据数值自动分配百分比

pie(x);

% 绘制第二张图像

subplot(1, 3, 2);

% 绘制饼图 , 绘制时根据数值自动分配百分比

% 后面跟着 有 x 相同个数的向量 ,

% 0 元素代表默认

% 1 元素代表分离出来

pie(x, [0, 0, 1, 0, 1]);

% 绘制第三张图像

subplot(1, 3, 3);

% 绘制 3D 饼图 , 绘制时根据数值自动分配百分比

% 后面跟着 有 x 相同个数的向量 ,

% 0 元素代表默认

% 1 元素代表分离出来

pie3(x, [0, 0, 1, 0, 1]);

绘图结果 :

十一、matlab中ut=[t,ones(size(t))]

ones(size(t))就是产生形状跟t一样的矩阵,但是矩阵的元素全是1

[t,ones(size(t))]就是将t与1写成一行.

比如t=[1;2;3;4];

那么ones(size(t))=[1;1;1;1];

两个合在一起就变成

1 1

2 1

3 1

4 1

相当于在原来t的后面加上一列.这一列全是t.

zeros函数：产生全0矩阵，即零矩阵。

ones函数：产生全1矩阵，即幺矩阵。

eye函数：产生对角线为1的矩阵。当矩阵是方阵时，得到一个单位矩阵。

rand函数：产生（0,1）区间均匀分布的随机矩阵。

randn函数：产生均值为0，方差为1的标准正态分布随机矩阵。

十二、用于专门学科的特殊矩阵

magic函数、vander函数、hilb函数、compan函数、pascal函数。

12.1魔方矩阵(方阵、magic函数)

<code>

>> M=magic(3)

M =

8 1 6

3 5 7

4 9 2

n阶魔方阵由1,2,3…,n共n2个整数组成，且每行、每列以及主、副对角线上各n个元素之和都相等。

n阶魔方阵每行每列元素的和为(1+2+3+…+n2) / n= (n+n3)/2。

Matlab中 magic(n) 只产生一个特定的魔方阵,实际上当n大于2时可能有多个魔方阵存在。

>> M=magic(3);

>> x=sum(M(1,:))

x =

15

>> y=sum(M(:,1))

y =

15

12.2范德蒙矩阵(方阵、vander函数)

在Matlab中，函数 vander(V) 生成以向量V为基础的范德蒙矩阵。

<code>>> A=vander(1:5)

A =

1 1 1 1 1

16 8 4 2 1

81 27 9 3 1

256 64 16 4 1

625 125 25 5 1

12.3希尔伯特矩阵(方阵、hilb函数)

<code>

>> H=hilb(4)

H =

1.0000 0.5000 0.3333 0.2500

0.5000 0.3333 0.2500 0.2000

0.3333 0.2500 0.2000 0.1667

0.2500 0.2000 0.1667 0.1429

format函数：控制输出格式。

format rat ：使用分数来表示数值

>> format rat

>> H=hilb(4)

H =

1 1/2 1/3 1/4

1/2 1/3 1/4 1/5

1/3 1/4 1/5 1/6

1/4 1/5 1/6 1/7

12.4伴随矩阵(方阵、compan函数)

Matlab生成伴随矩阵的函数是 compan()，其中p是一个多项式的系数向量，高次幂系数排在前，低次幂系数排在后。

<code>>> p=[1,-2,-5,6]; //对应 a3 a2 a1 a0，是一个3阶方阵

>> A=compan(p)

A =

2 5 -6

1 0 0

0 1 0

12.5帕斯卡矩阵(方阵、pascal函数)

<code>>> P=pascal(5)

P =

1 1 1 1 1

1 2 3 4 5

1 3 6 10 15

1 4 10 20 35

1 5 15 35 70

>> inv(P) //求矩阵P的逆矩阵

ans =

5.0000 -10.0000 10.0000 -5.0000 1.0000

-10.0000 30.0000 -35.0000 19.0000 -4.0000

10.0000 -35.0000 46.0000 -27.0000 6.0000

-5.0000 19.0000 -27.0000 17.0000 -4.0000

1.0000 -4.0000 6.0000 -4.0000 1.0000

十三、MATLAB中：冒号用法

13.1 x(:, :, : )

x(i,j,k)的含义是第k层矩阵的第i行第j列元素;

x(:,:,1)则表示第1层矩阵。

比如：创建多维数组

A = [1 2 3; 4 5 6; 7 8 9]

A(:,:,2) = [10 11 12; 13 14 15; 16 17 18]

那么，A就是

A =

A(:,:,1) =

1 2 3

4 5 6

7 8 9

A(:,:,2) =

10 11 12

13 14 15

16 17 18

A(:,1,1)

ans =

1

4

7

13.2 x(1, : )

y=x(1,:)，把x这个矩阵的第一行所有列赋给y。

注，冒号相当于所有。

13.3 x(:, : )

例如，在matlab中，a(:, 1:3)=[]表示将数组a的第1到第3列删除。

第一个冒号( : )表示取数组a的所有行；

1:3表示取数组a的第1到第3列。

十四、matlab中的findstr与strfind函数

matlab中这两个字符串查找的函数findstr(), strfind()表明上看起来用法相似，效果也相似。

14.1 findstr(s1,s2)

在较长的字符串中查找较短的字符串出现的次数，并返回其位置，因此无论s1,s2哪个为长字符串，位置在前在后都没有关系。

例：

s = 'Find the starting indices of the shorter string.';

findstr(s, 'the')

ans =

6 30

findstr('the', s)

ans =

6 30

14.2 strfind(s1,s2)

or strfind(s1,pattern),因此其意思在s1中搜索pattern，

例：

S = 'Find the starting indices of the pattern string';

strfind(S, 'in')

ans =

2 15 19 45

strfind(S, 'In')

ans =

[]

十五、Matlab rand（）函数用法

rand函数产生由在(0, 1)之间均匀分布的随机数组成的数组。

本人遇到的是matlab中的rand（a,b）语句，为了清楚这个语句的用法，这里我们随便输入a，b，例如1和4

回车之后结果为如图所示4个数字，可以看到这4个数均为1以内，且为1行4列

同样地，若我们输入rand(2,4)，则会得到一个2行4列的在1以内的随机矩阵

若想要得到一个3行3列的随机方阵，我们输入rand(3)即可

rand(size(A)) 返回一个和A有相同尺寸的随机矩阵。例如我们随便输入一个A矩阵，然后输入这个语句之后即可得到相同行列的一个随机矩阵

十六、MATLAB中squeeze函数的作用

订阅专栏

squeeze： 除去size为1的维度

B = squeeze(A)

描述：

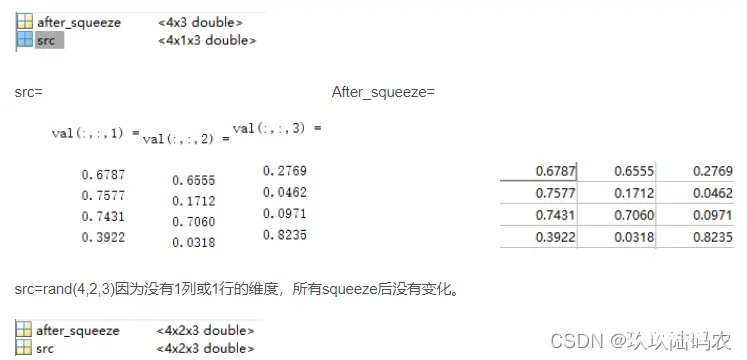
B = squeeze(A)， B与A有相同 元素,但所有只有一行或一列的维度（a singleton dimension）被去除掉了。二维阵列不受squeeze影响;

例如：

src=rand(4,1,3)产生一个均匀分布的阵列，共3页，每页4行1列，经过squeeze后，1列的那个维度就没有了，只剩下4行3列的一个二维阵列。

十七、Matlab之魔方阵magic

1、函数功能

magic函数是用于创建魔方阵。魔方阵的特点是：每行每列以及对角线的元素之和相等的方阵。

2、代码示例

<code>clc;

clear all;

A = magic(4)

sum(A(1,:)) %求第一行的元素之和

sum(A(:,1)) %求第一列的元素之和

sum(diag(A)) %求对角线的元素之和，diag函数生成主对角线元素的向量

运行结果：

A =

16 2 3 13

5 11 10 8

9 7 6 12

4 14 15 1

ans =

34

ans =

34

ans =

34

十八、Matlab的concur、repmat、kron、reshape函数介绍

18.1 concur

有时需要将某个列向量变成一个每列均相同的矩阵，这里就可以使用concur。

使用举例如下：

18.2 repmat函数

该函数也可以使用将某个列向量变成一个每列均相同的矩阵，进一步地还可以将矩阵复制。

使用举例如下：

更通用的使用例子如下：

18.3 kron函数

以上介绍的repmat的功能也可以使用kron实现，当然kron还可以实验更多功能。其实，kron函数是用来计算矩阵的克罗内克积(Kronecker product)的函数（有关克罗内克积可参见百度百科）。

其中repmat中的第1个例子可使用kron实现如下：

第2个例子可使用kron实现如下：

有时还想把矩阵的每一列(或行)分别复制n份，这里仍可以kron实现，如第一种实现bb=kron(aa,ones(1,3))将每一列复制了3份，而第二种实现bb=kron(aa,ones(3,1))将每一行复制了3份：

18.4 reshape

该函数可以将包含N个元素的m1n1矩阵变为m2n2的矩阵，reshape只改变矩阵的维度，输入参数要保证矩阵元素个数不变，即N=m1n1 = m2n2

注意矩阵变形时按列取值(whose elements are taken columnwise from X)，使用例子如下：

其中bb=reshape(aa,3,2)将23矩阵变成了32矩阵，而bb=reshape(aa,1,6)则变成为16的矩阵（行向量），注意在改变维度时是按列取值的。

使用reshape还可以实现更复杂的功能，例如要对一个34的矩阵按如下规则如始化：第1列第2个元素为1、第2列第3个元素为1、第3列第3个元素为1、第4列第1个元素为1，当然可以先初始化aa=zeros(2,3);然后再依次初始化各个元素的值，但在matlab里能矩阵化实现的尽量矩阵化实现，当矩阵较大时，节省的时间就感觉到了。这里实现如下：

18.5补充：矩阵向量化

说到reshape，补充一个Matlab常用的功能，就是将矩阵向量化，使用冒号即可，举例如下：

注意，在向量过程中，也是按列取值的，如果按行取值，则可以先将矩阵转置。

十九、Matlab之logspace

首先书上给的定义是logscape函数是用来创建指数等差数列，语法描述如下

logspace（x1，x2）——在从10^x1到10x2区间内生成含有50个元素的等差数列

logspace（x1，x2，n）——在从10^x1到10x2区间内生成含有n个元素的等差数列

解释一下，所谓的指数等差数列指的是指数部分是一个等差数列，给个例子

上图0—2中，3个元素的等差数列为{0，1，2}

所以输出的结果就是10^0,101,10^2，即1，10，100

另外，X1,X2支持float( double/single）型。

由于产生的是10的幂函数，所以广泛应用于生成频率。

二十、matlab的format指令

（1）format或者format short：短格式，在小数点后面显示四位有效数字。

（2）format long :长格式，16位有效数字。

（3）format compact :压缩格式，在显示变量之间，没有空行。

（4）format loose :宽松格式，在显示变量之间有空行。

二十一、matlab 中disp()常见用法

disp()函数在matlab中使用help指令得出的结果如下

disp - 显示变量的值

此 MATLAB 函数 显示变量 X 的值，而不打印变量名称。显示变量的另一种方法是键入它的名称，这种方法会在值前面显示一个前导X =。

disp(X)

既然参数只有一个那么分为3种：

【1】输出数字数组

例如：

<code>>>x = 3;

>>disp（x）

3

>>disp(5)

5

【2】输出字符串数组

例如：

>>str = ‘This is my first time’;

>>disp(str);

This is my first time

>>disp(‘Hello World!’);

Hello World!

【3】输出数字与字符串的混合

这里要先明白清楚，disp变量为X，若是有C语言经验等其他编程基础的同学，

可能想着找一个可以代替数字的符号或者将数字与字符串用符号连接一下就可以，

而disp()的变量类型固定，故我们需要变换类型

先看一个函数

num2str - 将数字转换为字符数组 此 MATLAB 函数

将数值数组转换为表示数字的字符数组。输出格式取决于原始值的量级。num2str 对使用数值为绘图添加标签和标题非常有用。

s = num2str(A)

s = num2str(A,precision)

s = num2str(A,formatSpec)

所以将数字转为字符串加入到我要输出的字符串数组即可

>>x = 1000;

>>str = ‘Hello World!’;

>>str = [str,num2str(x)];

>>disp(str)

Hello World!1000

二十二、Matlab mapminmax函数使用及原理

[Y,PS] = mapminmax(X)

[Y,PS] = mapminmax(X,FP)

Y = mapminmax(‘apply’,X,PS)

X = mapminmax(‘reverse’,Y,PS)

用实例来讲解,测试数据 x1 = [1 2 4], x2 = [5 2 3];

[y,ps] = mapminmax(x1)

y = -1.0000 -0.3333 1.0000

ps =

name: ‘mapminmax’

xrows: 1

xmax: 4

xmin: 1

xrange: 3

yrows: 1

ymax: 1

ymin: -1

yrange: 2

二十三、matlab 中num2str函数的使用

首先介绍一下num2str函数的使用方法，然后我们就知道该如何解决上面的问题了。调用形式如下：

1）str = num2str(A) ；

将数字A转换成char类型，值得注意的是A也可以是数字类型的数组。

a =[1,2,3,4];

y = num2str(a);

whos

2）str = num2str(A, precision)

A: 数值类型的数组或者是单个的数值

precision：转换成字符穿保留的数字位数

a = [1.222222,2.11111111,3.4444444];

y=num2str(a,2)

# 结果

y =

'1.2 2.1 3.4'

3）str = num2str(A, format)

A: 数值类型的数组或者是单个的数值

format:指定数字转换为字符串的格式，通常’%11.4g’是默认的。

也可以指定转换为几位的字符串，不足用0填充，如%02d

%03d等

a = 1;

y1 = num2str(a,'%02d'); % '01'

y2 = num2str(a,'%03d'); % '001'

看到该函数的第3种调用形式，我们就应该知道如何解决刚开始说的格式不一致的问题了。

files_path = './images/'; % 图像文件夹路径

img_path_list = dir(strcat(files_path,'*.tif'));

img_num = length(img_path_list)/2; % Pan和对应多光谱是一对

for index = 1:img_num

% 读取Pan和对应的多光谱图像

gt_name = img_path_list(index).name;% 获取图像名,只得到了多光谱图像

pan_name = ['pan_',num2str(index,'%02d'),'.tif'];

disp(gt_name); %测试

disp(pan_name);

disp('=============');

end

二十四、matlab遗传算法gatbx工具箱介绍及安装说明

安装步骤：把gatbx.rar解压至matlab安装目录下的toolbox文件夹里。运行matlab，在设置路径里添加该gatbx工具箱即可。

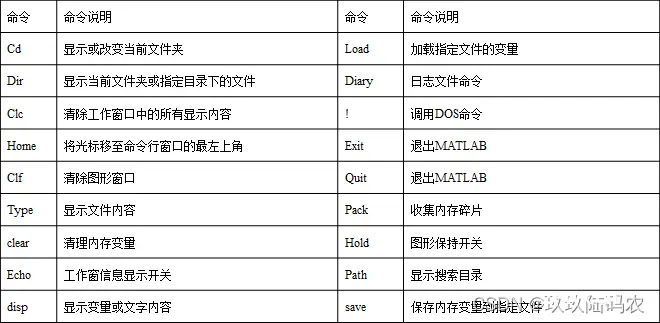
测试代码：

<code>%% matlab_gatbx_test.m

%遗传算法求f(x)=x*sin(10*pi*x)+2.0,在[-1,2]上的最大值

figure(1);

fplot(@(variable)variable.*sin(10*pi*variable)+2.0,[-1,2]); %画出函数曲线

%定义遗传算法参数

NIND=40; %个体数目(Number of individuals)

MAXGEN=25; %最大遗传代数(Maximum number of generations)

PRECI=20; %变量的二进制位数(Precision of variables)

GGAP=0.9; %代沟(Generation gap)说明子代与父代的重复率为0.1

trace=zeros(MAXGEN,2); %寻优结果的初始值

FieldD=[20;-1;2;1;0;1;1]; %区域描述器(Build field descriptor),第2、3行为自变量的下界和上界

Chrom=crtbp(NIND, PRECI); %定义初始种群

gen=0; %代计数器

variable=bs2rv(Chrom, FieldD); %计算初始种群的十进制转换

ObjV=shang(variable); %计算目标函数值

while gen<MAXGEN %进化MAXGEN代

FitnV=ranking(-ObjV); %分配适应度值(Assign fitness values)ranking函数的功能就是目标值越小的分配值越大，

%本例求解最大值，应该要是他的适应度值更大，故必须使得ranking内的数越小，这样分配的适应度值才能大

SelCh=select('sus', Chrom, FitnV, GGAP); %选择，使用sus方式，也可以改用rws方式

SelCh=recombin('xovsp', SelCh, 0.7); %重组，选用xovsp方式

SelCh=mut(SelCh); %变异

variable=bs2rv(SelCh, FieldD); %子代个体的十进制转换，把染色体变为十进制

ObjVSel=shang(variable); %计算子代的目标函数值

[Chrom ObjV]=reins(Chrom, SelCh, 1, 1, ObjV, ObjVSel); %重插入子代的新种群

variable=bs2rv(Chrom, FieldD); %子代个体的十进制转换，转为十进制

gen=gen+1; %代计数器增加

%输出最优解及其序号，并在目标函数图像中标出，Y为最优解,I为种群的序号

[Y, I]=max(ObjV);hold on;

plot(variable(I), Y, 'ro');

trace(gen,1)=max(ObjV); %遗传算法性能跟踪，把当代的最优值放入trace矩阵的第一行第目前代数列

trace(gen,2)=sum(ObjV)/length(ObjV); %把当代种群目标函数的均值，放入trace矩阵的第二行第目前代数列

end

variable=bs2rv(Chrom, FieldD); %最优个体的十进制转换，转回十进制，以便输出

hold on;

grid on;

plot(variable,ObjV,'b*');

figure(2);

plot(trace(:,1)); %把trace矩阵的第一列画出来（记录的是每一代的最优值）

hold on;

plot(trace(:,2),'-.');grid %把trace矩阵的第2列画出来（记录的是每一代种群目标函数均值）

legend('解的变化','种群均值的变化')

function z=shang(x) % 目标函数的核心部分（即缺省了优化目标的纯函数）

z=x.*sin(10*pi*x)+2.0;

end

%运行结果：

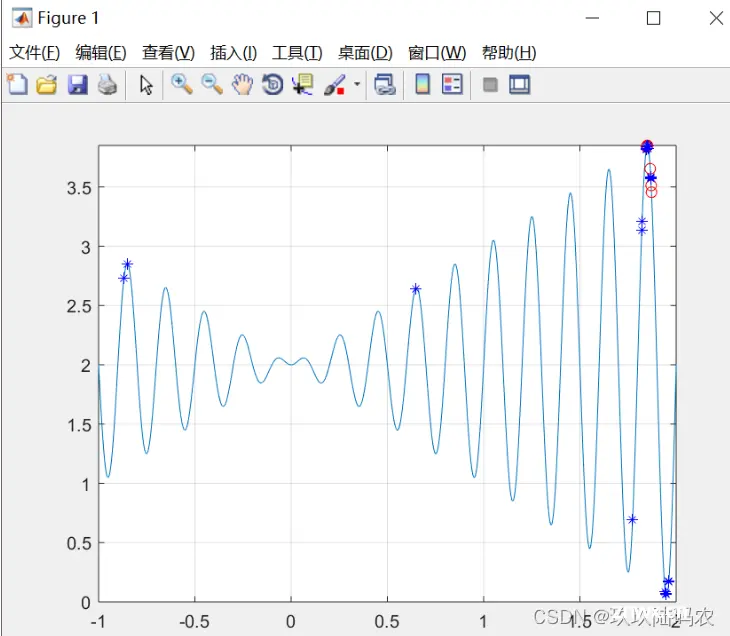
二十五、matlab的svm算法调试总结

【1】legend(’ ’ , ’ ’ , 3)，把3去掉

【2】princomp换成pca

因为princomp是老版的pca。