最长公共子序列

<li>本文讲解的题与leetcode1143.最长公共子序列这题一样，阅读完可以挑战一下。li>

力扣题目链接

题目叙述：

给定两个字符串，输出其最长公共子序列，并输出它的长度

输入：

ADABEC和DBDCA

输出：

DBC

3

解释

最长公共子序列是DBC，其长度为3

动态规划思路：

• 我们这题先构建一个模型，我们使用两个指针i,j ，分别用于遍历a字符串，b字符串。如图所示：

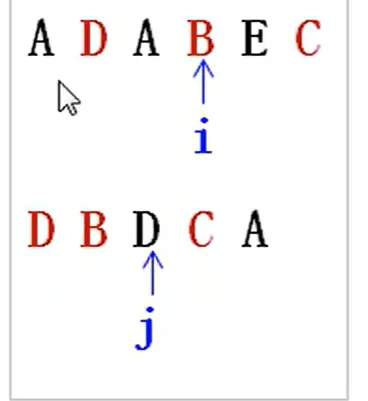
<li>

然后我们可以设想一个状态变量，也就是一个函数。一个关于两个变量相关的函数，这在代码中体现为二维数组<code>f。

li>

• 然后f[i][j]表示什么呢？表示序列a[1,2,3....i]和b[1,2,3....j]的最长公共子序列的长度

状态变量的含义

• 在这里的状态变量为f[i][j]，它的含义是a的前i个字符与b的前j个字符的最长公共子序列的长度

• 现在就要观察a[i],b[j]是否在当前的最长公共子序列当中。

• 具体情况如下图：

递推公式：

<li><code>f[i][j]可以分为三种情况讨论，就是：li>

1. a[i]，b[j]都在最长公共子序列当中，也就是a[i]==b[j]
2. a[i]!=b[j]，并且a[i]不在公共子序列当中。
3. a[i]!=b[j]，并且b[j]不在公共子序列当中。

• 那我们的递推公式就可与分为两种情况：
  • f[i][j]=f[i-1][j-1]+1 （a[i]==b[j]）
  • f[i][j]=max(f[i-1][j],f[i][j-1]) （a[i]!=b[j]）
• 显而易见，我们的边界条件为：
  • f[0][j]=0
  • f[i][0]=0

//m是a字符串的长度，n是b字符串的长度

for(int i=1;i<=m;i++){

for(int j=1;j<=n;j++){

//因为我们的f数组是从下标1开始，而字符串是从0开始的下标

if(a[i-1]==b[j-1]) f[i][j]=f[i-1][j-1]+1;

else f[i][j]=max(f[i-1][j],f[i][j-1]);

}

}

遍历顺序

• 经过上面的分析，明显遍历顺序为i从小到大，j也是从小到大 。

初始化

• 初始化边界为0即可

举例打印dp数组

• 如图所示

如何找出对应的最长公共子序列的长度

<li>

我们使用p数组来记录每一次<code>f[i][j]的值来源于哪一个方向

<li>1方向代表左上方
• 2方向代表左方
• 3方向代表上方

• 代码改造如下：

for(int i=1;i<=m;i++){

for(int j=1;j<=n;j++){

if(a[i-1]==b[j-1]){

f[i][j]=f[i-1][j-1]+1;

//左上方

p[i][j]=1;

}

else if(f[i-1][j]>f[i][j-1]){

f[i][j]=f[i][j-1];

//左边

p[i][j]=2;

}

else{

f[i][j]=f[i-1][j];

//上边

p[i][j]=3;

}

}

}

• p[i][j]代表前驱的位置。

算法的执行过程

• 我们要找到最长公共子序列，只需要找到从结尾开始，往前找到p[i][j]==1，也就是来源于左上方的哪些元素的集合，就是我们的最长公共子序列。（并不是棋盘中所有p[i][j]==1）的元素，而是从右下角出发，往回找到的所有p[i][j]==1的那些元素。
• 例子如下：

<li>

我们使用<code>s数组来储存最长公共子序列

li>

• 代码实现：

int i,j,k;

char s[200];

i=m;j=n;k=f[m][n];

while(i>0&&j>0){

//左上方

if(p[i][j]==1){

s[k--]=a[i-1];

i--;j--;

}

//左边

else if(p[i][j]==2) j--;

//上边

else i--;

}

for(int i=1;i<=f[m][n];i++) cout<<s[i];

最终代码实现：

#include <iostream>

#include <cstring>

using namespace std;

char a[200];

char b[200];

int f[205][205];

int p[205][205];

int m, n;

void LCS() {

int i, j;

m = strlen(a);

n = strlen(b);

for (i = 1; i <= m; i++) {

for (j = 1; j <= n; j++) {

if (a[i - 1] == b[j - 1]) {

f[i][j] = f[i - 1][j - 1] + 1;

p[i][j] = 1;

}

else if (f[i - 1][j] > f[i][j - 1]) {

f[i][j] = f[i - 1][j];

p[i][j] = 2;

}

else {

f[i][j] = f[i][j - 1];

p[i][j] = 3;

}

}

}

cout << f[m][n] << endl;

}

//寻找出当初的最长公共子序列。

void getLCS() {

int i = m, j = n, k = f[m][n];

char s[200];

s[k] = '\0';

while (i > 0 && j > 0) {

if (p[i][j] == 1) {

s[--k] = a[i - 1];

i--; j--;

}

else if (p[i][j] == 2) {

i--;

}

else {

j--;

}

}

cout << s << endl;

}

int main() {

cin >> a >> b;

LCS();

getLCS();

return 0;

}