交叉验证之KFold和StratifiedKFold的使用(附案例实战)
艾派森 2024-08-09 17:05:03 阅读 77

🤵♂️ 个人主页:@艾派森的个人主页
✍🏻作者简介:Python学习者
🐋 希望大家多多支持,我们一起进步!😄
如果文章对你有帮助的话,
欢迎评论 💬点赞👍🏻 收藏 📂加关注+

一、交叉验证简介
交叉验证是在机器学习建立模型和验证模型参数时常用的办法。交叉验证,顾名思义,就是重复的使用数据,把得到的样本数据进行切分,组合为不同的训练集和测试集,用训练集来训练模型,用测试集来评估模型预测的好坏。在此基础上可以得到多组不同的训练集和测试集,某次训练集中的某样本在下次可能成为测试集中的样本,即所谓“交叉”。
那么什么时候才需要交叉验证呢?交叉验证用在数据不是很充足的时候。通常情况下,如果数据样本量小于一万条,我们就会采用交叉验证来训练优化选择模型。如果样本大于一万条的话,我们一般随机的把数据分成三份,一份为训练集(Training Set),一份为验证集(Validation Set),最后一份为测试集(Test Set)。用训练集来训练模型,用验证集来评估模型预测的好坏和选择模型及其对应的参数。把最终得到的模型再用于测试集,最终决定使用哪个模型以及对应参数。
学习预测函数的参数,并在相同数据集上进行测试是一种错误的做法: 一个仅给出测试用例标签的模型将会获得极高的分数,但对于尚未出现过的数据它则无法预测出任何有用的信息。 这种情况称为 overfitting(过拟合).。为了避免这种情况,在进行机器学习实验时,通常取出部分可利用数据作为 test set(测试数据集) <code>X_test, y_test。下面是模型训练中典型的交叉验证工作流流程图。通过网格搜索可以确定最佳参数。
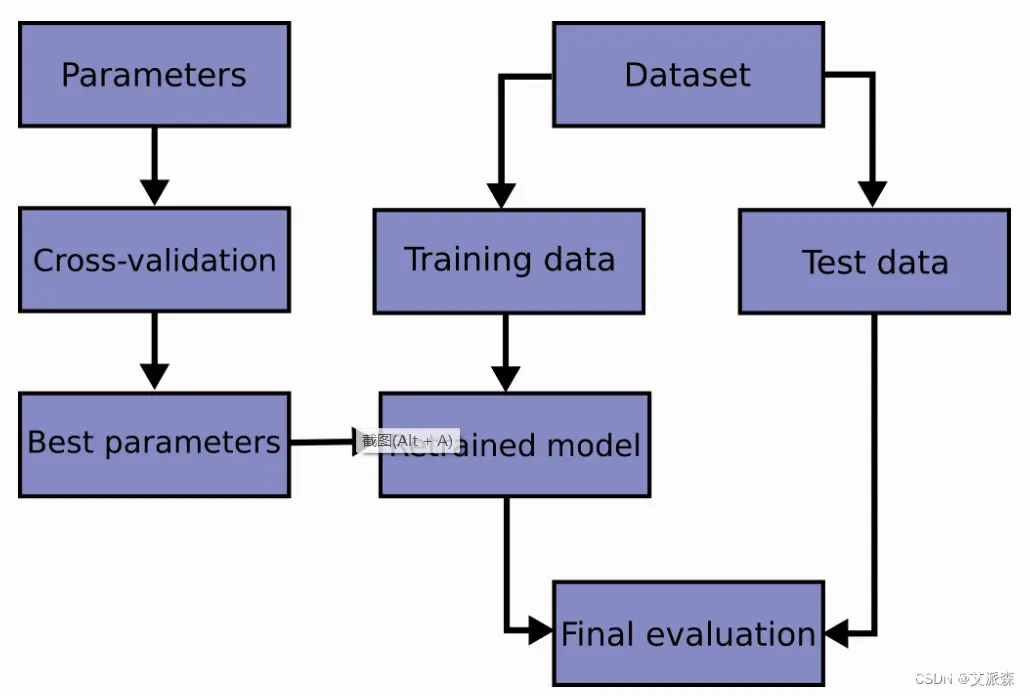
k-折交叉验证得出的性能指标是循环计算中每个值的平均值。 该方法虽然计算代价很高,但是它不会浪费太多的数据(如固定任意测试集的情况一样), 在处理样本数据集较少的问题(例如,逆向推理)时比较有优势。
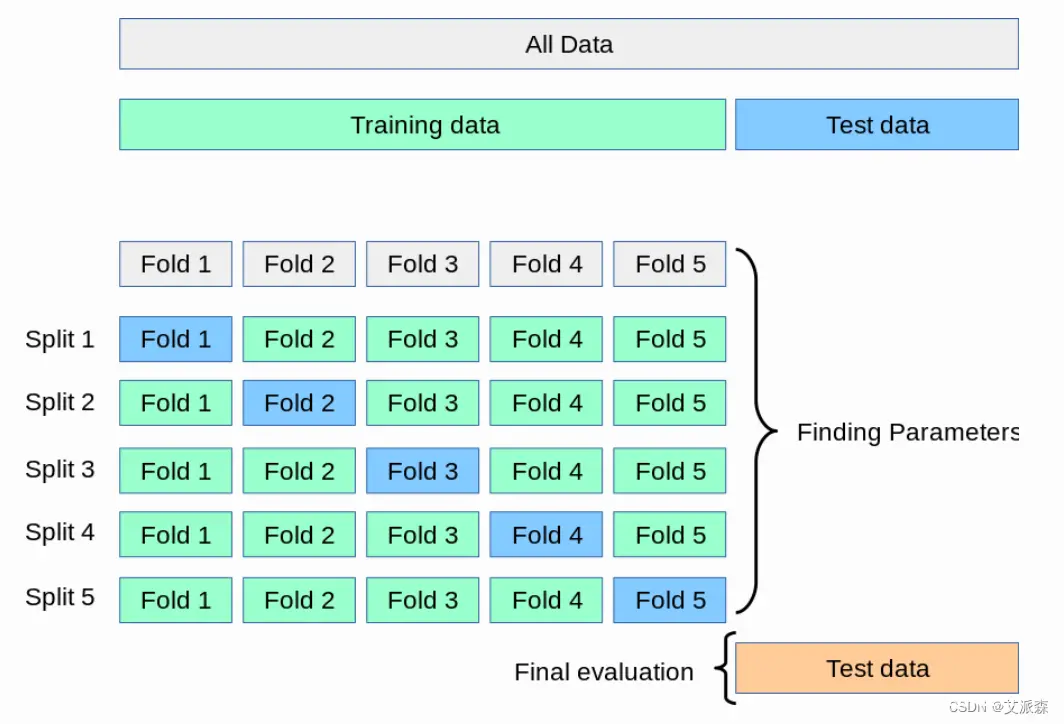
k-折交叉验证步骤
第一步,不重复抽样将原始数据随机分为 k 份。第二步,每一次挑选其中 1 份作为测试集,剩余 k-1 份作为训练集用于模型训练。第三步,重复第二步 k 次,这样每个子集都有一次机会作为测试集,其余机会作为训练集。在每个训练集上训练后得到一个模型,用这个模型在相应的测试集上测试,计算并保存模型的评估指标,第四步,计算 k 组测试结果的平均值作为模型精度的估计,并作为当前 k 折交叉验证下模型的性能指标。
例如:
十折交叉验证
将训练集分成十份,轮流将其中9份作为训练数据,1份作为测试数据,进行试验。每次试验都会得出相应的正确率。10次的结果的正确率的平均值作为对算法精度的估计,一般还需要进行多次10折交叉验证(例如10次10折交叉验证),再求其均值,作为对算法准确性的估计模型训练过程的所有步骤,包括模型选择,特征选择等都是在单个折叠 fold 中独立执行的。此外:
多次 k 折交叉验证再求均值,例如:10 次10 折交叉验证,以求更精确一点。数据量大时,k设置小一些 / 数据量小时,k设置大一些。

KFold和StratifiedKFold的使用
StratifiedKFold用法类似Kfold,但是它是分层采样,确保训练集,测试集中各类别样本的比例与原始数据集中相同。这一区别在于当遇到非平衡数据时,StratifiedKFold() 各个类别的比例大致和完整数据集中相同,若数据集有4个类别,比例是2:3:3:2,则划分后的样本比例约是2:3:3:2;但是KFold可能存在一种情况:数据集有5类,抽取出来的也正好是按照类别划分的5类,也就是说第一折全是0类,第二折全是1类等等,这样的结果就会导致模型训练时没有学习到测试集中数据的特点,从而导致模型得分很低,甚至为0。
Parameters
n_splits : int, default=3 也就是K折中的k值,必须大于等于2shuffle : boolean True表示打乱顺序,False反之random_state :int,default=None 随机种子,如果设置值了,shuffle必须为True
<code># KFold
from sklearn.model_selection import KFold
kfolds = KFold(n_splits=3)
for train_index, test_index in kfolds.split(X,y):
print('X_train:%s ' % X[train_index])
print('X_test: %s ' % X[test_index])
# StratifiedKFold
from sklearn.model_selection import StratifiedKFold
skfold = StratifiedKFold(n_splits=3)
for train_index, test_index in skfold.split(X,y):
print('X_train:%s ' % X[train_index])
print('X_test: %s ' % X[test_index])
KFold和StratifiedKFold实战案例
首先导入数据集,本数据集为员工离职数据,属于二分类任务
import pandas as pd
import warnings
warnings.filterwarnings('ignore')
data = pd.read_excel('data.xlsx')
data['薪资情况'].replace(to_replace={'低':0,'中':1,'高':2},inplace=True)
data.head()
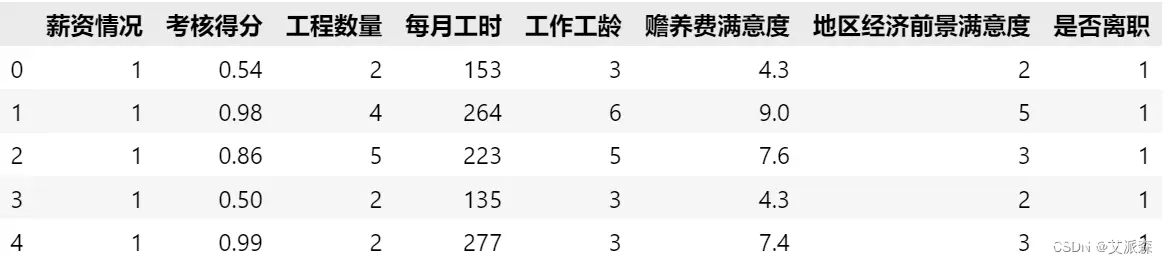
拆分数据集为训练集和测试集,测试集比例为0.2
<code>from sklearn.model_selection import train_test_split
X = data.drop('是否离职',axis=1)
y = data['是否离职']
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2)
初始化一个分类模型,这里用逻辑回归模型举例。方法1使用cross_val_score()可以直接得到k折训练的模型效果,比如下面使用3折进行训练,得分评估使用准确率,关于scoring这个参数我会在文末介绍。
# 初始化一个分类模型,比如逻辑回归
from sklearn.linear_model import LogisticRegression
lg = LogisticRegression()
# 方法1
from sklearn.model_selection import cross_val_score
scores = cross_val_score(lg,X_train,y_train,cv=3,scoring='accuracy')code>
print(scores)
print("Accuracy: %0.2f (+/- %0.2f)" % (scores.mean(), scores.std() * 2))
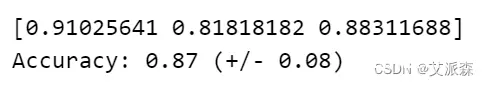
接下来分别使用KFold和StratifiedKFold,其实两者代码非常类似,只是前面的方法不同。
KFold
<code># 方法2-KFold和StratifiedKFold
import numpy as np
from sklearn.model_selection import KFold,StratifiedKFold
from sklearn.metrics import accuracy_score,recall_score,f1_score
# KFold
kfolds = KFold(n_splits=3)
accuracy_score_list,recall_score_list,f1_score_list = [],[],[]
for train_index,test_index in kfolds.split(X_train,y_train):
# 准备交叉验证的数据
X_train_fold = X_train.iloc[train_index]
y_train_fold = y_train.iloc[train_index]
X_test_fold = X_train.iloc[test_index]
y_test_fold = y_train.iloc[test_index]
# 训练模型
lg.fit(X_train_fold,y_train_fold)
y_pred = lg.predict(X_test_fold)
# 评估模型
AccuracyScore = accuracy_score(y_test_fold,y_pred)
RecallScore = recall_score(y_test_fold,y_pred)
F1Score = f1_score(y_test_fold,y_pred)
# 将评估指标存放对应的列表中
accuracy_score_list.append(AccuracyScore)
recall_score_list.append(RecallScore)
f1_score_list.append(F1Score)
# 打印每一次训练的正确率、召回率、F1值
print('accuracy_score:',AccuracyScore,'recall_score:',RecallScore,'f1_score:',F1Score)
# 打印各指标的平均值和95%的置信区间
print("Accuracy: %0.2f (+/- %0.2f)" % (np.average(accuracy_score_list), np.std(accuracy_score_list) * 2))
print("Recall: %0.2f (+/- %0.2f)" % (np.average(recall_score_list), np.std(recall_score_list) * 2))
print("F1_score: %0.2f (+/- %0.2f)" % (np.average(f1_score_list), np.std(f1_score_list) * 2))

StratifiedKFold
<code># StratifiedKFold
skfolds = StratifiedKFold(n_splits=3)
accuracy_score_list,recall_score_list,f1_score_list = [],[],[]
for train_index,test_index in skfolds.split(X_train,y_train):
# 准备交叉验证的数据
X_train_fold = X_train.iloc[train_index]
y_train_fold = y_train.iloc[train_index]
X_test_fold = X_train.iloc[test_index]
y_test_fold = y_train.iloc[test_index]
# 训练模型
lg.fit(X_train_fold,y_train_fold)
y_pred = lg.predict(X_test_fold)
# 评估模型
AccuracyScore = accuracy_score(y_test_fold,y_pred)
RecallScore = recall_score(y_test_fold,y_pred)
F1Score = f1_score(y_test_fold,y_pred)
# 将评估指标存放对应的列表中
accuracy_score_list.append(AccuracyScore)
recall_score_list.append(RecallScore)
f1_score_list.append(F1Score)
# 打印每一次训练的正确率、召回率、F1值
print('accuracy_score:',AccuracyScore,'recall_score:',RecallScore,'f1_score:',F1Score)
# 打印各指标的平均值和95%的置信区间
print("Accuracy: %0.2f (+/- %0.2f)" % (np.average(accuracy_score_list), np.std(accuracy_score_list) * 2))
print("Recall: %0.2f (+/- %0.2f)" % (np.average(recall_score_list), np.std(recall_score_list) * 2))
print("F1_score: %0.2f (+/- %0.2f)" % (np.average(f1_score_list), np.std(f1_score_list) * 2))

补充
<code>scoring 参数: 定义模型评估规则
Model selection (模型选择)和 evaluation (评估)使用工具,例如 model_selection.GridSearchCV 和 model_selection.cross_val_score ,采用 scoring 参数来控制它们对 estimators evaluated (评估的估计量)应用的指标。
常见场景: 预定义值
对于最常见的用例, 可以使用 scoring 参数指定一个 scorer object (记分对象); 下表显示了所有可能的值。 所有 scorer objects (记分对象)遵循惯例 higher return values are better than lower return values(较高的返回值优于较低的返回值)。因此,测量模型和数据之间距离的 metrics (度量),如 metrics.mean_squared_error 可用作返回 metric (指数)的 negated value (否定值)的 neg_mean_squared_error 。
| Scoring(得分) | Function(函数) | Comment(注解) |
|---|---|---|
| Classification(分类) | ||
| ‘accuracy’ | metrics.accuracy_score | |
| ‘average_precision’ | metrics.average_precision_score | |
| ‘f1’ | metrics.f1_score | for binary targets(用于二进制目标) |
| ‘f1_micro’ | metrics.f1_score | micro-averaged(微平均) |
| ‘f1_macro’ | metrics.f1_score | macro-averaged(宏平均) |
| ‘f1_weighted’ | metrics.f1_score | weighted average(加权平均) |
| ‘f1_samples’ | metrics.f1_score | by multilabel sample(通过 multilabel 样本) |
| ‘neg_log_loss’ | metrics.log_loss | requires predict_proba support(需要 predict_proba 支持) |
| ‘precision’ etc. | metrics.precision_score | suffixes apply as with ‘f1’(后缀适用于 ‘f1’) |
| ‘recall’ etc. | metrics.recall_score | suffixes apply as with ‘f1’(后缀适用于 ‘f1’) |
| ‘roc_auc’ | metrics.roc_auc_score | |
| Clustering(聚类) | ||
| ‘adjusted_mutual_info_score’ | metrics.adjusted_mutual_info_score | |
| ‘adjusted_rand_score’ | metrics.adjusted_rand_score | |
| ‘completeness_score’ | metrics.completeness_score | |
| ‘fowlkes_mallows_score’ | metrics.fowlkes_mallows_score | |
| ‘homogeneity_score’ | metrics.homogeneity_score | |
| ‘mutual_info_score’ | metrics.mutual_info_score | |
| ‘normalized_mutual_info_score’ | metrics.normalized_mutual_info_score | |
| ‘v_measure_score’ | metrics.v_measure_score | |
| Regression(回归) | ||
| ‘explained_variance’ | metrics.explained_variance_score | |
| ‘neg_mean_absolute_error’ | metrics.mean_absolute_error | |
| ‘neg_mean_squared_error’ | metrics.mean_squared_error | |
| ‘neg_mean_squared_log_error’ | metrics.mean_squared_log_error | |
| ‘neg_median_absolute_error’ | metrics.median_absolute_error | |
| ‘r2’ | metrics.r2_score |
声明
本文内容仅代表作者观点,或转载于其他网站,本站不以此文作为商业用途
如有涉及侵权,请联系本站进行删除
转载本站原创文章,请注明来源及作者。