1.安装Matplotlib和NumPy库

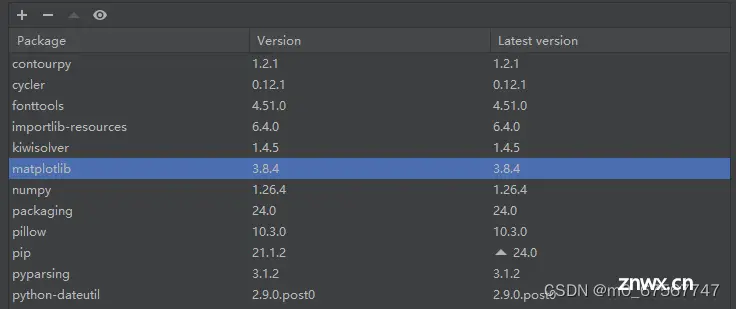
1）Matplotlib库的使用

Matplotlib库由各种可视化类构成,内部结构复杂,受Matlab启发。matplotlib.pyplot是绘制各类可视化图形的命令子库

2）引入pyplot子库

import matplotlib.pyplot as plt

2.常用方法

1）plt.figure()方法

创建画布，可以通过参数指定它的大小和背景颜色：

plt.figure(figsize=None, facecolor=None)

2）plt.subplot()

在全局绘图区域绘制一个子图

plt.subplot(nrows, ncols, index, **kwargs)

3个参数，分别代表网格的行数 nrows，列数 ncols，索引号index。它们都是位置参数。

plt.subplot(pos, **kwargs)

3位数的整数，每一位分别代表网格的行数，列数 ，索引号。pos也是是位置参数。

plt.subplot(**kwargs)

用默认值创建一个子图。

plt.subplot(ax)

以一个axes为参数，创建子图。

3）plt.axes(rect,axisbg='w')

创建一个坐标系风格的子图，用rect参数指定位置，用axisbg参数指定背景颜色。

4）plt.rcParams

plt.rcParams["font.sans-serif"]=["SimHei"] # 设置字体为黑体

plt.rcParams["axes.unicode_minus"]=False # 防止负号乱码

Matplotlib库默认是不支持中文的，使用中文会产生乱码，如果要使用中文可以在导入库后加入下列两行代码来临时修改配置文件

5）plt.title()和plt.suptitle()

用plt.title()方法为子图添加标题，也可以使用plt.suptitle()方法为当前绘图区域添加中心标题。

6）plt.xlabel(s)和plt.ylabel(s)

使用plt.xlabel(s)和plt.ylabel(s)方法可以分别设置当前x轴和y轴的标签。

7）plt.grid()

使用plt.grid()方法可以设置图表中的网格线：

plt.grid(b=None, which='major', axis='both', **kwargs)

b：可选，默认为 None，可以设置布尔值，true 为显示网格线，false 为不显示，如果设置 **kwargs 参数，则值为 true。

which：可选，可选值有 ‘major’、‘minor’ 和 ‘both’，默认为 ‘major’，表示应用更改的网格线。

axis：可选，设置显示哪个方向的网格线，可以是取 ‘both’（默认），‘x’ 或 ‘y’，分别表示两个方向，x 轴方向或 y 轴方向。

**kwargs：可选，设置网格样式，可以是 color=‘r’, linestyle=‘-’ 和 linewidth=2，分别表示网格线的颜色，样式和宽度。

8）plt.plot()

使用plt.plot()方法可以绘制曲线图，语法结构如下：

plt.plot(x, y, format_string, **kwargs)

plt.plot(x,y1,'b-v')

x：可选，表示X轴数据，类型为列表或数组。

y：表示Y轴数据，类型为列表或数组。

format_string：可选，由颜色字符、线条字符、标记字符组成。

**kwargs：多组(x,y,format_string)，绘制多条曲线。

               

9）绘制常见图表

plt.plot() 绘制折线图

plt.scatter() 绘制散点图

plt.bar() 绘制柱状图

plt.barh() 绘制横向柱状图

plt.stem() 绘制火柴图

plt.step() 绘制阶梯图

plt.hist() 绘制直方图

plt.boxplot() 绘制箱线图

plt.errorbar() 绘制误差条图

plt.violinplot() 绘制小提琴图

plt.eventplot()  绘制尖峰栅格图

plt.hist2d() 绘制二维直方图/散点密度图

plt.hexbin() 绘制Hexbin散点图

plt.pie() 绘制扇形图

官方文档：

Matplotlib — Visualization with Python

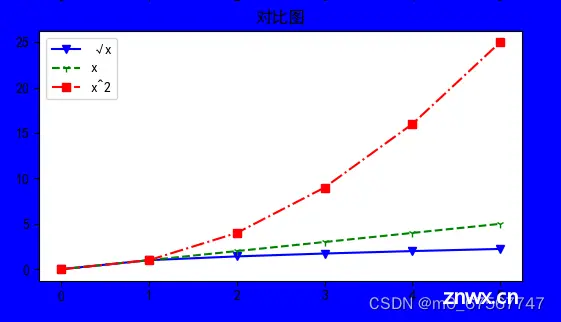
10）plt.legend()和plt.figlegend()

plt.legend()方法为子图添加图例，也可以使用plt.figlegend()方法为全局绘图区域添加图例，传入一个列表参数来给每条线命名。

plt.legend(["√x", "x", "x^2"])

plt.figlegend(["√x", "x", "x^2"])

11）plt.savefig()和plt.show()

使用plt.savefig()方法可以保存当前图像，参数为文件保存路径及文件名。使用plt.show()方法可以显示当前图像。

3.绘制简单函数图像

1）y = x^2

<code>import numpy as np

import matplotlib.pyplot as plt

# 1、准备函数

x = np.linspace(-10, 10, 400) # 生成一个x的值，从-10到10，包含400个点

y = x ** 2

# 2、绘制坐标

plt.plot(x, y)

# 3、设置图像标题和轴标签

plt.title('y = x^2')

plt.xlabel('X')

plt.ylabel('Y')

# 4、展示图像

plt.show()

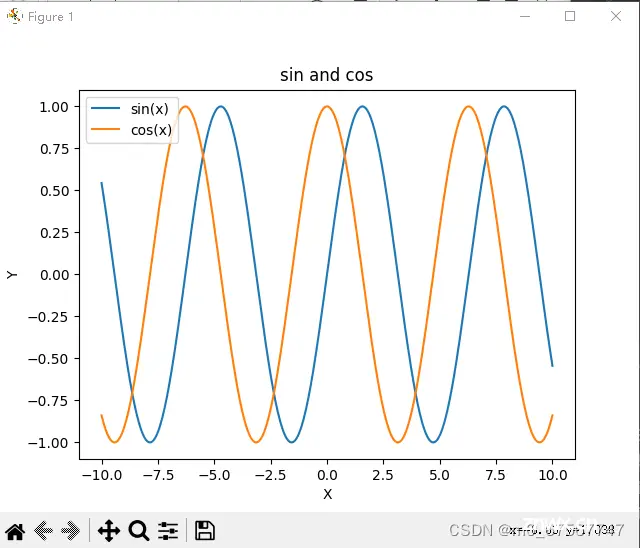
2）三角函数

<code>import numpy as np

import matplotlib.pyplot as plt

# 1、准备函数

x = np.linspace(-10, 10, 400) # 生成一个x的值，从-10到10，包含400个点

y_sin = np.sin(x)

y_cos = np.cos(x)

# 2、绘制坐标

plt.plot(x, y_sin, label='sin(x)')code>

plt.plot(x, y_cos, label='cos(x)')code>

# 3、设置图像标题和轴标签

plt.title('sin and cos')

plt.xlabel('X')

plt.ylabel('Y')

plt.legend()

# 4、展示图像

plt.show()

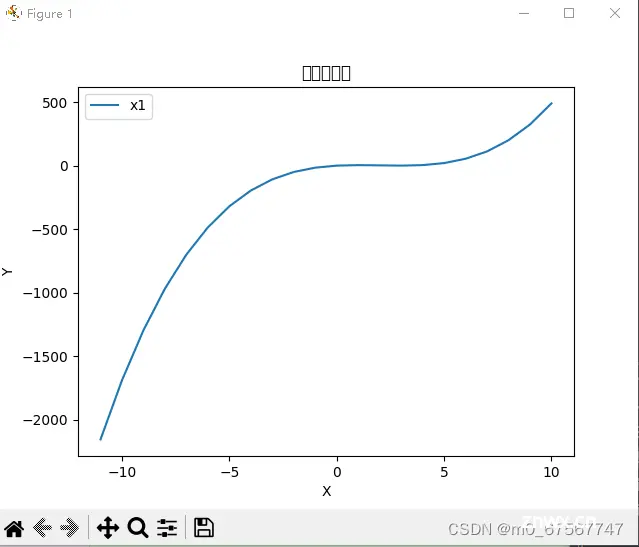
3）多项式函数：y = x**3 - 6*x**2 + 9*x + 1

<code>import matplotlib.pyplot as plt

# 1、准备函数

f1 = lambda x:x**3 - 6 * x ** 2 + 9 * x + 1

x = list(range(-11, 11))

y = [f1(i) for i in x]

# 2、绘制坐标

# 3、设置图像标题和轴标签

plt.plot(x, y, label="多项式")code>

plt.title("多项式函数")

plt.xlabel("X")

plt.ylabel("Y")

plt.legend(["x1"]) # 子图添加图例

# 4、展示图像

plt.show()

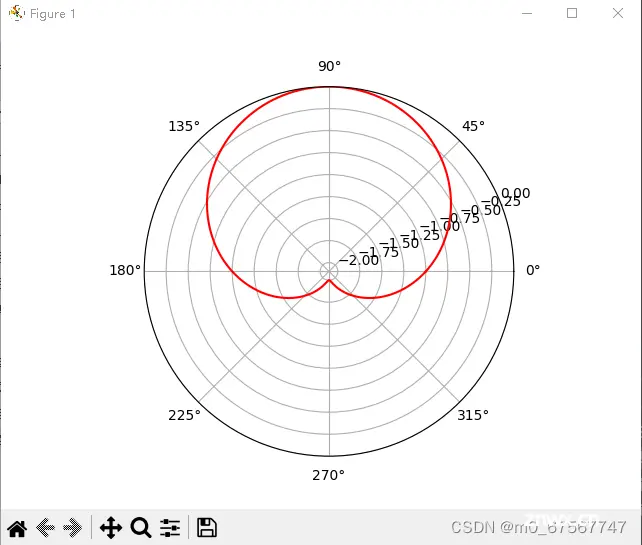
4）极坐标

<code>import numpy as np

import matplotlib.pyplot as plt

# 极坐标方程

# r = a(1−sinθ)

# 1、准备函数

theta = np.linspace(0, 2*np.pi, 1000) # 生成一个x的值，包含400个点

r = -1 * (1 - np.sin(theta)) # 心型线

# 2、绘制坐标

gra = plt.subplot(111, polar=True) # 在全局绘图区域绘制一个子图

gra.plot(theta, r, color='red') # plt.plot()方法可以绘制曲线图code>

# 3、展示图像

plt.show()

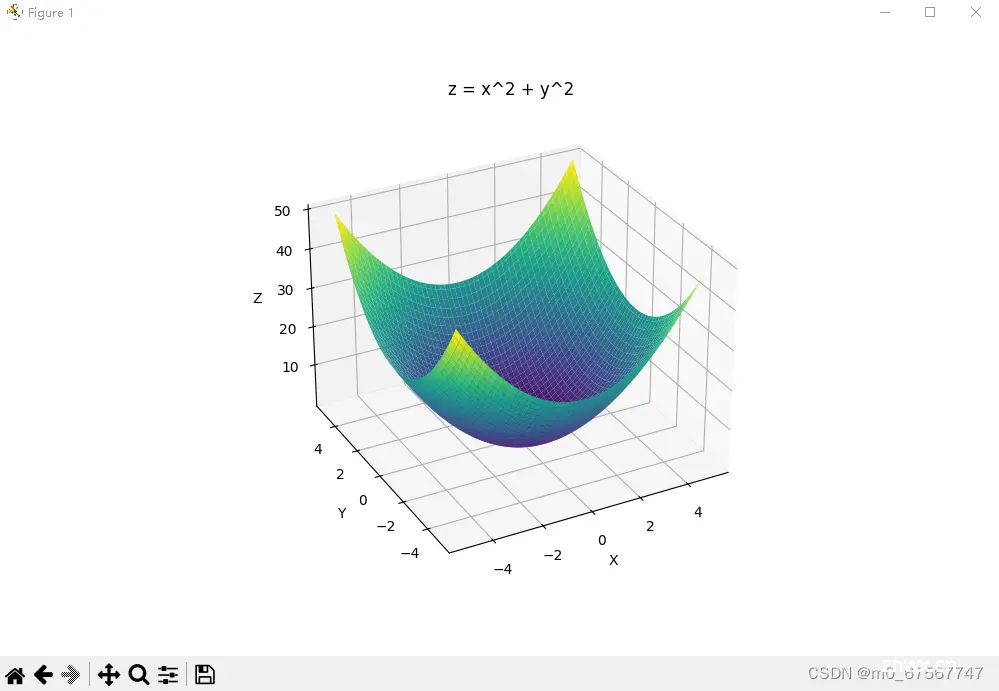
4.绘制3D图像

<code>import numpy as np

import matplotlib.pyplot as plt

# 1、生成坐标

x = np.linspace(-5, 5, 100) # x取值范围

y = np.linspace(-5, 5, 100) # y取值范围

X, Y = np.meshgrid(x, y)

# 2、定制函数

def simple_func(x, y):

return X**2 + Y**2

# 3、计算函数值

Z = simple_func(X, Y)

# 4、绘制图像

fig = plt.figure(figsize=(10, 8))

ax = fig.add_subplot(111, projection="3d")code>

ax.plot_surface(X, Y, Z, cmap='viridis')code>

ax.set_xlabel('X')

ax.set_ylabel('Y')

ax.set_zlabel('Z')

ax.set_title('z = x^2 + y^2')

plt.show()