1. 官方文档

math --- 数学函数 — Python 3.12.2 文档

cmath --- 关于复数的数学函数 — Python 3.12.2 文档

Python 中，可以使用内置的数学运算符，例如加法 (+)、减法 (-)、除法 (/) 和乘法 (*) 进行简单的数学运算。不过，更高级的运算，如指数函数、对数函数、三角函数或幂函数，并没有内置函数，需要使用 Python 标准库中一个专门为高级数学运算设计的模块：math 模块。

 2. 常量

 代码说明：

<code>math.pi

# 3.141592653589793

math.tau

# 6.283185307179586

math.e

# 2.718281828459045

math.inf

# inf

math.nan

# nan

math.pi * 2 == math.tau

# True

float('inf') == math.inf

# True

math.inf == math.inf

# True

math.inf == -math.inf

# False

float('nan') == math.nan

# False

math.isnan(math.nan)

# True

math.isnan(float('nan'))

# True

3. 数论与表示函数

3.1 函数概览

3.2 细节

（1）math.factorial(n)

import timeit

import math

# 阶乘的三种实现方式

# 1. for循环

def fact_loop(num):

if num < 0:

return 0

if num == 0:

return 1

factorial = 1

for i in range(1, num+1):

factorial = factorial * i

return factorial

print(fact_loop(15))

# 1307674368000

# 2. 递归函数

def fact_recursion(num):

if num < 0:

return 0

if num == 0:

return 1

return num * fact_recursion(num - 1)

print(fact_recursion(15))

# 1307674368000

# 3. math.factorial

print(math.factorial(15))

# 1307674368000

timeit.timeit("fact_loop(15)", globals=globals()) # 0.8621199000044726

timeit.timeit("fact_recursion(15)", globals=globals()) # 2.6800807999970857

timeit.timeit("math.factorial(15)", setup="import math") # 0.17294190000393428code>

从执行时间来看，递归方法是三种方法中最慢的，factorial() 明显比其他方法更快，这得益于它的底层用 C 实现。不同CPU可能得到不同的计时结果，但耗时大小的顺序应该是一样的。

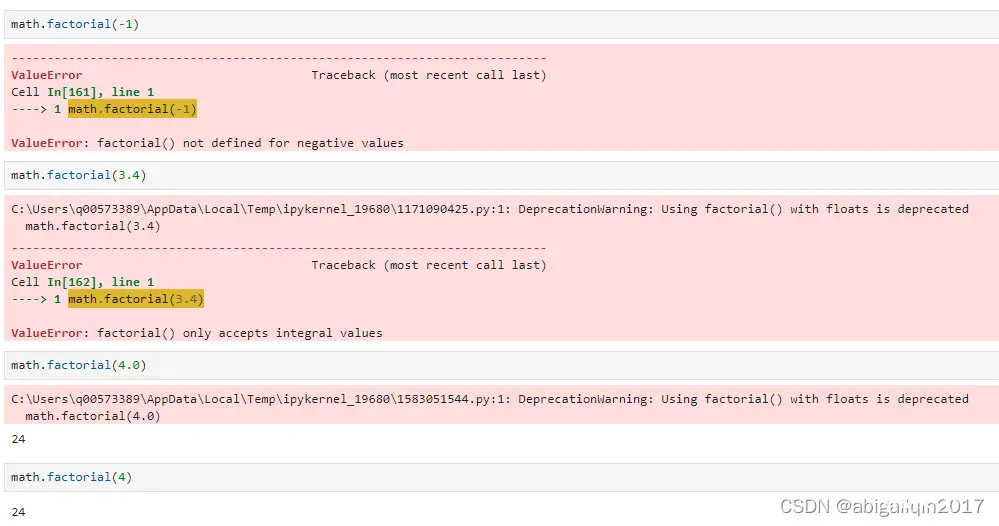
factorial() 不仅比其他方法快，而且更稳定。自己手写函数时，需要显式地为异常情况编写代码，例如处理负数或小数。但当使用 factorial() 时，因为函数会处理所有异常情况，建议尽可能使用 factorial()。

（2）math.ceil(x)、math.floor(x)、math.trunc(x)、math.modf(x)

<code>math.ceil(4.896)

# 5

math.ceil(-7.956)

# -7

math.ceil(4)

# 4

math.ceil(-7)

# -7

math.floor(4.896)

# 4

math.floor(-7.956)

# -8

math.floor(4)

# 4

math.floor(-7)

# -7

math.trunc(4.9)

# 4

math.trunc(-11.7)

# -11

math.trunc(4)

# 4

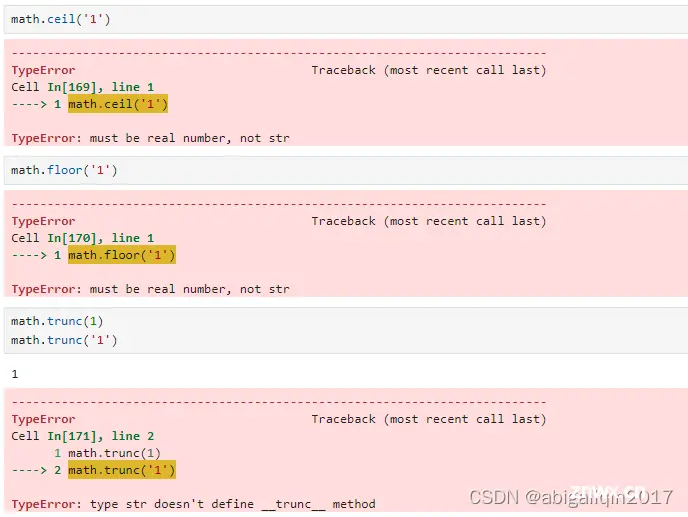
<code>import math

math.modf(-4.123)

# (-0.12300000000000022, -4.0)

（3）math.isclose()

import math

math.isclose(6, 7)

# False

math.isclose(6.999999999, 7)

# True

math.isclose(6.999999992, 7)

# False

math.isclose(6.9999999963, 7)

# True

math.isclose(6, 7, rel_tol=0.2)

# True

math.isclose(5.6, 7, rel_tol=0.2)

# False

math.isclose(5.61, 7, rel_tol=0.2)

# True

math.isclose(6, 7, abs_tol=1.0)

# True

math.isclose(6, 7, abs_tol=0.2)

# False

math.isclose(1, 1+1e-08, abs_tol=1e-08)

# True

math.isclose(1, 1-1e-08, rel_tol=1e-08)

# False

math.isclose(1, 1-1e-08+1e-09, rel_tol=1e-08)

# True

特殊情况：

import math

math.isclose(math.nan, 1e308)

# False

math.isclose(math.nan, math.nan)

# False

math.isclose(math.inf, 1e308)

# False

math.isclose(math.inf, math.inf)

# True

（4）math.fabs(x)

import math

abs(-1.234)

abs(1)

abs(3+4j)

math.fabs(-1.234)

math.fabs(1)

math.fabs(3+4j)

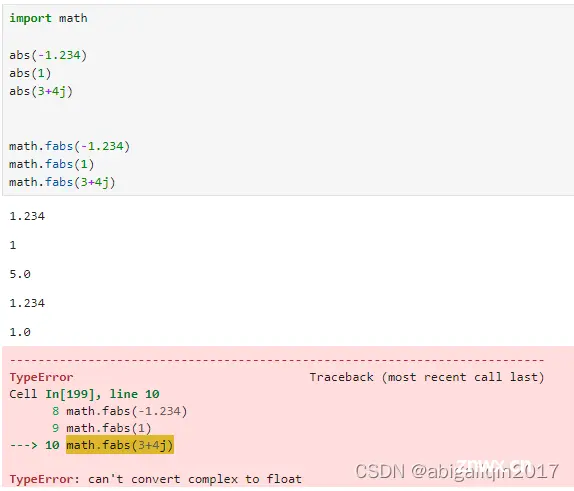
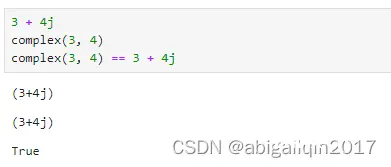
在 Python 中，复数可以使用 `j` 或 `J` 表示虚部。例如，3 + 4j 表示实部为 3，虚部为 4 的复数。Python 还提供了一个内置函数 complex 用于创建复数：complex(3, 4) 返回值等同于 3 + 4j。

可以使用 type() 函数来检查一个变量是否为复数类型，例如， type(3+4j) 返回结果为：complex。复数的绝对值是一个数的大小，不考虑其正负（绝对值是一个数的物理意义上的‘长度’或‘大小’，不受正负影响）。对于一个复数，比如 a+bi,它的绝对值是|a+bi|=sqrt(a^2+b^2)。

（5）math.lcm(x)、math.gcd(x)

<code>import math

math.lcm(2,3,6)

# 6

math.gcd(15,2)

# 1

math.gcd(15,3)

# 3

（6）math.fsum(iterable)、math.prod(iterable, start=1)

<code>list1 = [1.0, 2.0 , 3.3, 4.5]

list2 = [2, 2, 2, 2]

math.fsum(list1)

# 29.7

math.prod(list1, start=1)

# 29.7

math.prod(list1, start=2)

# 59.4

（7）math.isqrt(x)、math.frexp(x)、math.ldexp(x, i)

import math

math.frexp(5)

# (0.625, 3)

math.ldexp(0.625, 3)

# 5.0

math.isqrt(7)

# 2

math.isqrt(9)

# 3

math.frexp(x) 的应用场景包括：

将一个浮点数转换为二进制表示时，可以使用 math.frexp() 将其分解为尾数和指数的形式，方便进行计算和存储。

在科学计算、信号处理等领域中，经常需要对浮点数进行归一化处理，即将其表示为尾数乘以某个基数的指数形式。此时可以使用 math.frexp() 将浮点数分解为尾数和指数，然后将尾数除以基数，指数加上相应的偏移量，得到归一化后的结果。 

在一些算法中，需要对浮点数进行比较和排序。由于浮点数的精度有限，直接比较可能会出现误差。此时可以使用 math.frexp() 将浮点数分解为尾数和指数，然后按照指数大小进行比较和排序，可以避免精度误差的影响。

（8）math.fmod(x,y)

import math

x, y = -9, 4

x % y

# 3

math.fmod(x, y)

# -1.0

math.remainder(x, y)

# -1.0

下面这个例子中，使用 % 时得到了奇怪的结果，此时更适合用 math.fmod()。

import math

math.fmod(-2, 10) # 返回值：-2.0

-2 % 10 # 返回值：8

math.fmod(10, 1e+10) # 返回值：10.0

10 % 1e+10 # 返回值：10.0

math.fmod(-10, 1e+10) # 返回值：-10.0

-10 % 1e+10 # 返回值：9999999990.0

# 一个使用 % 得到的结果很奇怪的例子

-1e-100 % 1e+100 # 返回值：1e+100

# 事实上，返回的结果应该是是1e100-1e-100, 但这个值无法表示成一个浮点数, 近似的表示成了1e100

# the result of Python’s -1e-100 % 1e100 is 1e100-1e-100, which cannot be represented exactly as a float, and rounds to the surprising 1e100.

math.fmod(-1e-100, 1e+100) # 返回值：-1e-100

# 使用math.fomd得到的结果显然更为合理。

（9）其他

import math

math.comb(4, 3)

# 4

math.perm(4, 3)

# 24

math.copysign(-2.3, 4.5)

# 2.3

math.copysign(2.3, -4.5)

# -2.3

math.copysign(-2.3, 0)

# 2.3

math.copysign(-2.3, -0)

# 2.3

4. 幂函数

细节

（1）math.pow(x,y)

Python 中，除了math.pow，还有两种方法计算幂：内置函数 pow(x, y[,z]) 和 x ** y。

内置函数 pow 可接收三个参数：The base number，The power number，The modulus number

最后一个参数是可选的，如果传递了第三个参数 z，返回结果将是：(x ** y) % z，

下面的代码显示了三种函数的使用效果以及耗时情况（math.pow 底层基于C实现，因而最快）。

import math

math.pow(1, math.nan) # 1.0

math.pow(1, math.inf) # 1.0

math.pow(1, 0) # 1.0

math.pow(math.nan, 0) # 1.0

math.pow(math.inf, 0) # 1.0

math.pow(1, 0) # 1.0

# math.pow(0, -1) # ValueError: math domain error

math.pow(0, math.nan) # nan

math.pow(0, math.inf) # 0.0

math.pow(0, 0) # 1.0

import math

import timeit

# 内置函数 pow(x, y[,z])

pow(2, 3) # 8

pow(2, 3, 3) # 2

pow(-2, 3) # 8

pow(-2, 3, 3) # 1

(-2 ** 3) % 3 # 1

# x ** y

2 ** 3 # 8

# 比较三种函数耗时

timeit.timeit("9 ** 293")

timeit.timeit("pow(9, 293)")

timeit.timeit("math.pow(9, 293)", setup="import math")code>

# 返回结果：

# 0.7688344000000029

# 0.8183434000000034

# 0.20894989999999325

（2）math.exp(x)