目录

一、中心对数比变换的定义二、中心对数比变换的原理三、中心对数比变换的作用四、应用领域五、scikit-bio介绍

一、中心对数比变换的定义

中心对数比变换（Centered Log Ratio Transformation，CLR）是一种数据预处理方法，常用于<code>成分数据分析领域。在成分数据中，各成分之间通常存在一定的约束关系，比如它们的和为固定值等，中心对数比变换可以有效地处理这种具有特殊约束的数据。

二、中心对数比变换的原理

对于一个具有(D)个成分的成分数据向量

x

=

(

x

1

,

x

2

,

⋯

,

x

D

)

\boldsymbol{x}=(x_1,x_2,\cdots,x_D)

x=(x1​,x2​,⋯,xD​)，且满足

∑

i

=

1

D

x

i

=

C

\sum_{i = 1}^{D}x_i = C

∑i=1D​xi​=C

(

C

(C

(C为常数）。首先计算中心比：

对于

i

=

2

,

3

,

⋯

,

D

i = 2,3,\cdots,D

i=2,3,⋯,D，中心比

y

i

=

x

i

g

(

x

)

y_i=\frac{x_i}{g(x)}

yi​=g(x)xi​​，其中

g

(

x

)

=

∏

j

=

1

D

x

j

D

−

1

g(x)=\sqrt[D - 1]{\prod_{j = 1}^{D}x_j}

g(x)=D−1∏j=1D​xj​

​，是几何均值。 然后进行对数变换：

得到

z

i

=

ln

⁡

y

i

=

ln

⁡

x

i

g

(

x

)

z_i=\ln y_i=\ln\frac{x_i}{g(x)}

zi​=lnyi​=lng(x)xi​​，

i

=

2

,

3

,

⋯

,

D

i = 2,3,\cdots,D

i=2,3,⋯,D，通常取

z

1

=

0

z_1 = 0

z1​=0（为了满足约束条件的一种设定）。

三、中心对数比变换的作用

改善数据的分布特性

可以将原本可能具有复杂分布的成分数据转化为更接近正态分布或其他便于分析的分布形式，从而更适合后续的统计分析和建模工作。 消除成分之间的冗余信息

由于成分数据之间存在约束关系，直接使用原始数据可能会导致信息冗余和多重共线性等问题。对数中心比变换可以在一定程度上消除这些问题，使得每个变量所携带的信息更加独立和有效。 便于进行比较和分析

经过变换后的数据在数值上更加规整，不同成分之间的差异和关系更加清晰，有利于进行各种比较和分析操作。 解决成分数据的闭合效应

成分数据由于其和为固定值（如 1）的约束，存在闭合效应，这会导致在某些常规统计方法中出现问题。例如，在进行多元线性回归时，由于这种闭合效应，直接使用原始成分数据可能会得到不合理的结果。中心对数比变换将成分数据进行转换，打破了这种闭合效应，使得后续的统计分析更加合理和准确。

四、应用领域

地质学

在地球化学研究中，对岩石、土壤等样本的化学成分分析通常会得到成分数据，如各种元素的含量比例。中心对数比变换可以用于处理这些成分数据，以便更好地揭示不同样本之间的化学成分差异和地质成因关系。 生物学

在生态学中，对于生态群落的物种组成数据，其各物种的相对丰度构成成分数据。通过中心对数比变换，可以分析不同生态环境下物种组成的变化规律和相互关系。 经济学

在一些经济指标的分析中，如消费结构、产业结构等，其不同部分的比例关系也可以看作成分数据。中心对数比变换可以帮助经济学家更好地理解和分析这些经济结构的变化和影响因素。

以下是一个简单的 Python 代码示例来实现中心对数比变换：

import numpy as np

import math

def log_centered_ratio_transform(data):

D = data.shape[0]

# 计算几何平均值 g(x)

g = (np.prod(data))**(1/(D - 1))

transformed_data = np.zeros(D - 1)

for i in range(1, D):

y = data[i] / g

transformed_data[i - 1] = math.log(y)

return transformed_data

使用以下方式调用函数：

# 示例数据，假设有 4 个成分，总和为 1

data = np.array([0.2, 0.3, 0.1, 0.4])

transformed = log_centered_ratio_transform(data)

print(transformed)

五、scikit-bio介绍

官方文档

scikit-bio是一个在Python3中处理生物数据的库

成分统计 (skbio.stats.composition )模块中的skbio.stats.composition.clr，此函数将组合从Aitchison几何体转换到真实空间。这个clr变换既是定义在下列空间上的等距变换，又是同构变换

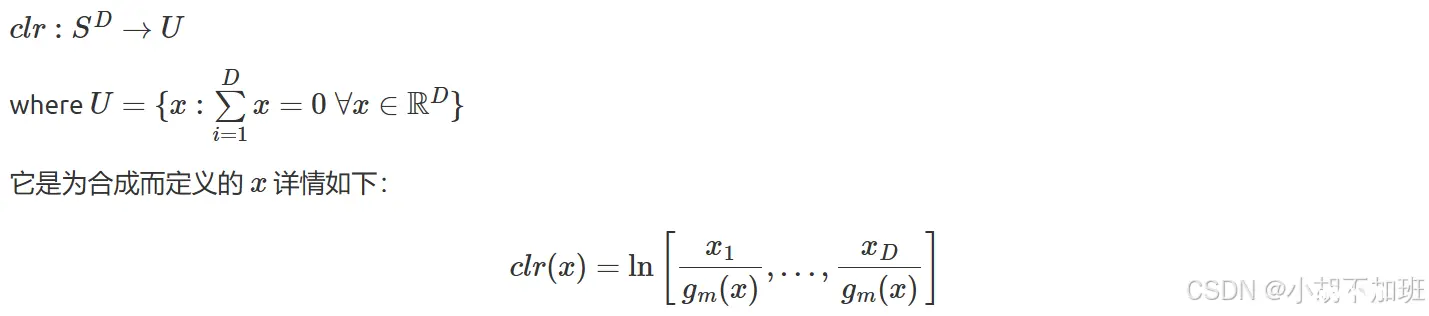
示例

<code>import numpy as np

from skbio.stats.composition import clr

x = np.array([.1, .3, .4, .2])

clr(x)