一、课程设计目的

通过请求页式管理方式中页面置换算法的模拟设计，了解虚拟存储技术的特点，掌握请

求页式存储管理中的页面置换算法。

二、课程设计内容

模拟实现

OPT

（最佳置换）、

FIFO

和

LRU

算法，并计算缺页率。

三、要求及提示

1

、首先用随机数生成函数产生一个“指令将要访问的地址序列”，然后将地址序列变换

成相应的页地址流（即页访问序列），再计算不同算法下的命中率。

2

、通过随机数产生一个地址序列，共产生

400

条。其中

50%

的地址访问是顺序执行的，

另外

50%

就是非顺序执行。且地址在前半部地址空间和后半部地址空间均匀分布。具体产

生方法如下：

1)

在前半部地址空间，即

[0

，

199]

中随机选一数

m

，记录到地址流数组中（这是

非顺序执行）；

2)

接着“顺序执行一条指令”，即执行地址为

m+1

的指令，把

m+1

记录下来；

3)

在后半部地址空间，

[200

，

399]

中随机选一数

m’

，作为新指令地址；

4)

顺序执行一条指令，其地址为

m’+1

；

5)

重复步骤

1~4

，直到产生

400

个指令地址。

3

、将指令地址流变换成页地址（页号）流，简化假设为：

1)

页面大小为

1K

（这里

K

只是表示一个单位，不必是

1024B

）；

2)

用户虚存容量为

40K

；

7

3)

用户内存容量为

4

个页框到

40

个页框；

4)

用户虚存中，每

K

存放

10

条指令，所以那

400

条指令访问地址所对应的页地

址（页号）流为：指令访问地址为

[0

，

9]

的地址为第

0

页；指令访问地址为

[10

，

19]

的地址为第

1

页；……。按这种方式，把

400

条指令组织进“

40

页”，并

将“要访问的页号序列”记录到页地址流数组中。

4

、循环运行，使用户内存容量从

4

页框到

40

页框。计算每个内存容量下不同页面置换

算法的命中率，命中率

=1-

缺页率。输出结果可以为：

页框数

OPT

命中率

FIFO

命中率

LRU

命中率

[4] OPT

：

0.5566 FIFO

：

0.4455 LRU

：

0.5500

[5] OPT

：

0.6644 FIFO

：

0.5544 LRU

：

0.5588

……

……

……

……

[39] OPT

：

0.9000 FIFO

：

0.9000 LRU

：

0.9000

[40] OPT

：

1.0000 FIFO

：

1.0000 LRU

：

1.0000

注

1

：在某一次实验中，可能

FIFO

比

LRU

性能更好，但足够多次的实验表明

LRU

的平均性能比

FIFO

更好。

注

2

：计算缺页率时，以页框填满之前和之后的总缺页次数计算。

需求分析

(1)输入的形式和输入值的范围

         地址序列生成:

                随机数生成器用于产生地址序列，范围为 [0, 399] 的整数，共计 400 条指令地址。

                地址序列的生成应满足题目中描述的规则，即 50% 的地址是顺序执行的，另外 50% 是非顺序执行的，并在前半部地址空间 [0, 199] 和后半部地址空间 [200, 399] 中均匀分布。

        页框数量:

                用户内存容量为 4 到 40 个页框，需要循环遍历这些数量以计算不同内存大小下的命中率。

        页面大小与用户虚存容量:

                页面大小为 1K。

                用户虚存容量为 40K。

(2)    输出的形式

        输出应为表格形式，显示不同页框数下 OPT、FIFO 和 LRU 算法的命中率。

        命中率可以通过 1 - 缺页率 计算得出。

        输出:

                页框数 OPT 命中率 FIFO 命中率 LRU 命中率  

                [4]    OPT：0.xxxx FIFO：0.xxxx LRU：0.xxxx   

                [5]    OPT：0.xxxx FIFO：0.xxxx LRU：0.xxxx   

                ...  

                [40]   OPT：1.0000 FIFO：1.0000 LRU：1.0000

(3)程序所能达到的功能

         程序应能模拟请求页式管理方式中的页面置换算法，包括 OPT、FIFO和 LRU算法。

         程序应能计算并输出在不同内存大小下，各页面置换算法的命中率。

        程序应能处理生成的地址序列，将其转换为页地址流，并模拟页面置换过程。

(4)测试数据：包括正确的输入及其输出结果和含有错误的输入及其输出结果

        输入: 无（地址序列生成规则，页框数量从 4 到 40）

        输出: 如上所示的命中率表格，每个算法在不同页框数下的命中率

概要设计 

(1)    抽象数据类型定义

        指令流（instruct）：

                类型：列表（List）

                元素：整数（Integer）

                描述：存储模拟产生的指令地址序列，每个地址通过除以10转换为页号。

        用户内存（user_mem）：

                类型：列表（List）

                元素：整数（Integer）

                描述：模拟的物理内存中的页号，存储最近使用或选定的页面。

        访问频率计数（temp）：

                类型：列表（List）

                元素：整数（Integer）

                描述：在LFU算法中，用于记录用户内存中每个页面在过去一段时间内的访问频率。

        结果矩阵（result）：

                类型：NumPy数组（Array）

                元素：浮点数（Float）

                描述：存储不同页面数量（n）下，各个页面置换算法（FIFO、LRU、OPT、LFU）的命中率。

(2)    主程序流程

        调用produceAddstream()函数生成指令地址序列，并转换为页号流。

        初始化一个NumPy数组result，用于存储不同页面数量下的各种算法命中率。

        通过循环，遍历从4到40的页面数量（n）。

        对于每个n，分别调用OPT(n, ins)、FIFO(n, ins)、LRU(n, ins)和LFU(n, ins)函数计算各种算法的命中率。

        将结果存储在result数组中，并打印出来。

        使用matplotlib库绘制命中率随页面数量变化的图形，并显示图例。

        调用plt.show()显示图形。

(3)    模块间层次关系

        主程序（main()）：

                调用produceAddstream()生成指令流。

                初始化结果矩阵result。

                循环遍历页面数量，调用OPT()、FIFO()、LRU()和LFU()函数计算命中率。

                打印结果。

                调用matplotlib库绘制图形并显示。

        produceAddstream()：

                生成并返回指令地址序列。

        OPT(n, ins)、FIFO(n, ins)、LRU(n, ins)、LFU(n, ins)：

                输入：页框数量n和指令流ins。

                根据不同的页面置换算法逻辑，遍历指令流，计算命中率。

                返回命中率。

调用关系图

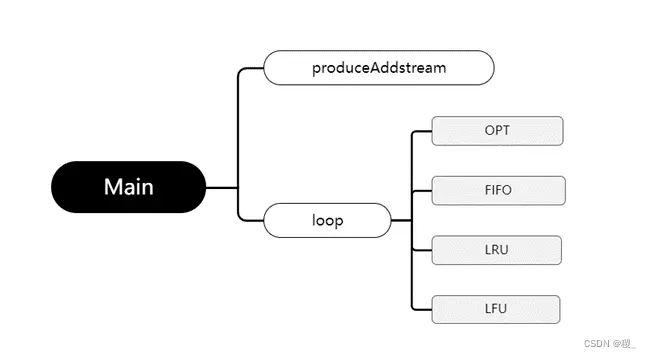
用户使用说明 

        本程序用于比较和分析四种不同的页面替换算法：OPT（最佳页面替换算法）、FIFO（先进先出）、LRU（最近最少使用）和LFU（最少使用频率）。这些算法在模拟的缓存环境中运行，以评估它们在不同缓存大小（k）下的性能。

1. 安装必要的库

2. 运行程序

        本程序包含一个main函数，它负责生成指令流、执行四种页面替换算法，并打印结果。可以直接运行这个程序，无需任何命令行参数。

3. 生成结果

        程序会打印出一个表格，其中包含缓存大小（k）从4到40以及每种算法在对应缓存大小下的命中率。表格的列标题分别是“k”、“FIFO”、“LRU”、“OPT”和“LFU”。每一行表示一个特定的缓存大小，以及在该缓存大小下每种算法的命中率。

4. 修改参数

        可以修改produceAddstream函数来改变指令流的生成方式。

        在main函数中，x = np.arange(4, 41)定义了缓存大小的范围，可以根据需要修改这个范围。

        result = np.zeros([4, 37])定义了一个用于存储结果的二维数组。这个数组的大小根据想要比较的算法数量和缓存大小范围来调整。

5. 注意事项

        性能：对于较大的缓存大小和指令流长度，程序可能需要一些时间来运行。这是因为页面替换算法需要对每个页面引用进行迭代和计算。

        结果分析：可以根据打印出的表格来分析不同算法在不同缓存大小下的性能。通常，OPT算法会表现出最高的命中率，因为它总是选择未来最不可能被引用的页面进行替换。FIFO和LRU算法的性能通常较差，因为它们不考虑页面的使用频率或未来引用模式。

运行结果（局部图片）：

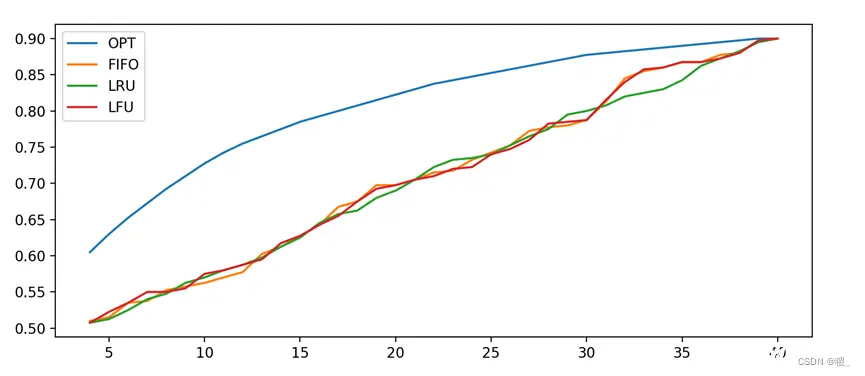
源代码（参考）：

<code>import numpy as np

import matplotlib.pyplot as plt

def produceAddstream():

instruct = []

m = np.random.randint(0, 399)

for i in range(100):

instruct.append(m+1)

n = np.random.randint(0, m+1)

instruct.append(n)

instruct.append(n+1)

m = np.random.randint(n+2, 399)

instruct.append(m)

return instruct

def FIFO(n, ins):

user_mem = []

hit = 0

for i in ins:

if i // 10 in user_mem:

hit += 1

else:

if len(user_mem) == n:

user_mem.pop(0)

user_mem.append(i // 10)

return hit / len(ins)

def OPT(n, ins):

hit = 0

user_mem = []

dic = dict.fromkeys(range(40), [])

for (ind, i) in enumerate(ins):

dic[i // 10] = dic[i // 10] + [ind]

for (ind, i) in enumerate(ins):

dic[i // 10].pop(0)

if (i // 10) in user_mem:

hit += 1

else:

if len(user_mem) == n:

temp = [401] * n

for (index, page) in enumerate(user_mem):

if len(dic[page]) > 0:

temp[index] = dic[page][0]

user_mem.pop(np.argmax(temp))

user_mem.append(i // 10)

return hit / len(ins)

def LRU(n, ins):

user_mem = []

hit = 0

for i in ins:

if i // 10 in user_mem:

hit += 1

temp = user_mem.pop(user_mem.index(i//10))

user_mem.append(temp)

else:

if len(user_mem) == n:

user_mem.pop(0)

user_mem.append(i//10)

return hit / len(ins)

def LFU(n, ins):

user_mem = []

hit = 0

for (ind, i) in enumerate(ins):

if i // 10 in user_mem:

hit += 1

else:

if len(user_mem) == n:

temp = [0] * n

for item in ins[max(0, ind - 20):ind]:

for k in range(n):

if user_mem[k] == item // 10:

temp[k] += 1

break

user_mem.pop(np.argmin(temp))

user_mem.append(i // 10)

return hit / len(ins)

def main():

ins = produceAddstream()

result = np.zeros([4, 37])

x = np.arange(4, 41)

print('k FIFO LRU OPT LFU')

for i in x:

result[0, i-4] = OPT(i, ins)

result[1, i-4] = FIFO(i, ins)

result[2, i-4] = LRU(i, ins)

result[3, i-4] = LFU(i, ins)

print(i,' ',result[0, i-4],' ',result[1, i-4],' ',result[2, i-4],' ',result[3, i-4])

plt.figure(figsize=(10, 4))

plt.plot(x, result[0], label="OPT")code>

plt.plot(x, result[1], label="FIFO")code>

plt.plot(x, result[2], label="LRU")code>

plt.plot(x, result[3], label="LFU")code>

plt.legend()

plt.show()

return

main()