个人主页

文章目录

⭐前言🏠一、priority-queue的介绍🎄二、priority-queue的使用🎡三、priority-queue的模拟实现1. 基本框架2. 向上调整3. 向下调整

🚀四、仿函数的介绍priority-queue中的仿函数

🏝️五、总结及源代码priority-queue.cpp

⭐前言

首先在进入优先级队列的学习之前，我们需要先对优先级队列有一定的了解。

优先级队列是容器适配器中的一种，元素在队列中的顺序是按照它们的优先级来排列的，而不是按照它们被插入的队列的顺序。这其实就是数据结构中的堆，其底层都是以数组存储的完全二叉树，下面就来详细了解一下priority-queue是如何进行使用的。

🏠一、priority-queue的介绍

Priority Queue（优先级队列） 是一种特别的数据结构，它为队列中的每个元素都分配了一个优先级。在这个队列里，元素并非按照被插入的顺序来排列，而是依据它们的优先级来排序。这意味着，具有最高优先级的元素会最先被处理或移除，而优先级最低的元素则会最后被处理。它的底层实现通常使用堆这一数据结构。

🎄二、priority-queue的使用

优先级队列默认使用vector作为其底层存储数据的容器，在vector上又使用了堆算法将vector中元素构造成堆的结构，因此priority_queue就是堆，所有需要用到堆的位置，都可以考虑使用priority_queue。注意：默认情况下priority_queue是大堆。

🎡三、priority-queue的模拟实现

我们还是根据库中操作，把它实现成一个容器适配器的类模板：

<code>namespace bit

{ -- -->

template<class T,class Container = vector<T>>

class priority_queue

{

public：

private:

Container _con;

};

}

后面会讲到第三个模板参数及比较的仿函数。

1. 基本框架

我们首先来实现一下它的基本核心接口：

1.push

我们在push的时候先尾插一个数据，然后在对它进行向上调整操作。

void push(const T& x)

{

_con.push_back(x);

Adjustup(_con.size() - 1);

}

2.pop

我们在之前实现堆的删除时，是不是将堆顶的数据跟最后一个数据进行交换，然后删除数组的最后一个数据，最后再进行向下调整操作。

void pop()

{

swap(_con[0], _con[_con.size() - 1]);

_con.pop_back();

AdjustDown(0);

}

3.top

返回队列的第一个数据。

const T& top()

{

return _con[0];

}

4.size

返回队列中有效数据的大小

size_t size() const

{

return _con.size();

}

5.empty

判断队列是否为空

bool empty() const

{

return _con.empty();

}

2. 向上调整

我们默认先按大堆来进行调整。

向上调整之前要保证之前的数据必须是一个堆。插入的数据首先会被放置在堆的末尾，然后看插入的数据是否满足对应大堆的性质，不满足就进行交换，直到满足就停止。

void Adjustup(int child)

{

int parent = (child - 1) / 2;

while (child > 0)

{

if (_con[parent] < _con[child])

{

swap(_con[child], _con[parent]);

child = parent;

parent = (child - 1) / 2;

}

else

{

break;

}

}

}

3. 向下调整

其调整思路和向上调整类似，只不过它是从上往下进行调整。

过程：从根节点开始选出左右孩子节点较小的那一个，让父亲节点与该节点进行比较，如果小于该节点则进行交换，大于则不交换，不断循环此过程，直到符合父亲节点大于等于孩子节点时则停止。

void AdjustDown(int parent)

{

size_t child = parent * 2 + 1;

while (child < _con.size())

{

if (child + 1 < _con.size() && _con[child] < _con[child + 1])

{

++child;

}

if (_con[parent] < _con[child])

{

swap(_con[child], _con[parent]);

parent = child;

child = parent * 2 + 1;

}

else

{

break;

}

}

}

🚀四、仿函数的介绍

仿函数（Functor）是一种编程概念，它指的是一种重载了函数调用运算符operator()的类或结构体，因从而可以像普通函数一样被调用。

priority-queue中的仿函数

我们在上述实现了默认是大堆的情况下，如果我们想要小堆该怎么办呢?

之前我们在学习堆的过程中就知道，只需把向上或向下调整的比较符号改成相反的就可以了。但是我们通过学习仿函数，我们就可以通过传仿函数去控制大小堆的变化。

template<class T>

class Less

{

public:

bool operator()(const T& x, const T& y)

{

return x < y;

}

};

template<class T>

class Greater

{

public:

bool operator()(const T& x, const T& y)

{

return x > y;

}

};

我们默认Less是大堆，Greater是小堆。

那我们该怎么使用第三个参数呢?我们只需和库中保持一致即可，默认第三个参数为

class compare的缺省参数为仿函数Less即可。

template<class T,class Container = vector<T>,class compare = Less<T>>

class priority_queue

{

public:

//向上调整

void Adjustup(int child)

{

compare com;

int parent = (child - 1) / 2;

while (child > 0)

{

//if (_con[parent] < _con[child])

if(com(_con[parent] , _con[child]))

{

swap(_con[child], _con[parent]);

child = parent;

parent = (child - 1) / 2;

}

else

{

break;

}

}

}

//向下调整

void AdjustDown(int parent)

{

size_t child = parent * 2 + 1;

compare com;

while (child < _con.size())

{

//if (child + 1 < _con.size() && _con[child] < _con[child + 1])

if (child + 1 < _con.size() && com(_con[child] , _con[child + 1]))

{

++child;

}

//if (_con[parent] < _con[child])

if(com(_con[parent], _con[child]))

{

swap(_con[child], _con[parent]);

parent = child;

child = parent * 2 + 1;

}

else

{

break;

}

}

}

这样做我们就可以通过仿函数来控制大小堆的变化。

我们下面就可以通过代码来演示一下：

现在先用默认为大堆的情况下：

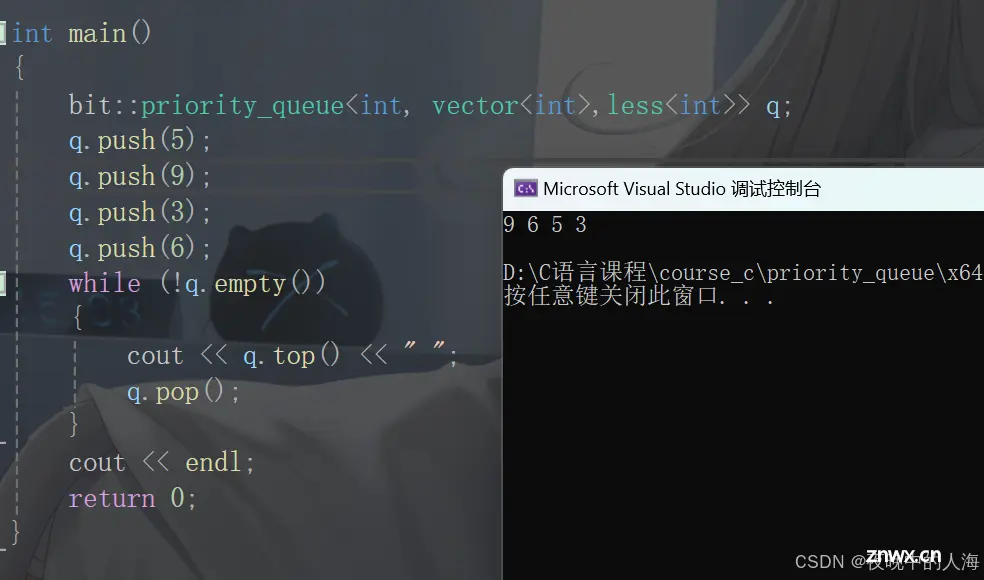
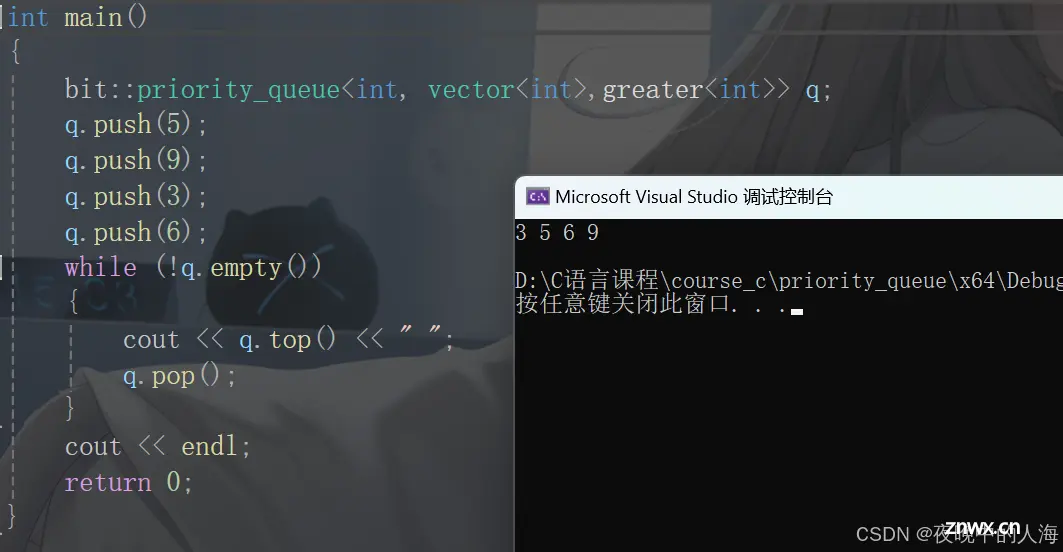
如果我们想要在小堆的情况下，只需把less改成greater即可。

🏝️五、总结及源代码

通过上述学习，我们总结一下知识点：

1.优先级队列是一种容器适配器，其底层就是堆这一结构。

2.默认情况下，优先级队列为大堆。

3.队列中的元素具有优先级，优先级高的元素先出队。优先级相同的元素则按照先进先出的方式处理。

4.允许队列在任意位置插入数据，但出队时则先移除优先级较高的元素。

priority-queue.cpp

<code>template<class T>

class Less

{ -- -->

public:

bool operator()(const T& x, const T& y)

{

return x < y;

}

};

template<class T>

class Greater

{

public:

bool operator()(const T& x, const T& y)

{

return x > y;

}

};

namespace bit

{

template<class T,class Container = vector<T>,class compare = Less<T>>

class priority_queue

{

public:

void Adjustup(int child)

{

compare com;

int parent = (child - 1) / 2;

while (child > 0)

{

if(com(_con[parent] , _con[child]))

{

swap(_con[child], _con[parent]);

child = parent;

parent = (child - 1) / 2;

}

else

{

break;

}

}

}

void push(const T& x)

{

_con.push_back(x);

Adjustup(_con.size() - 1);

}

void AdjustDown(int parent)

{

size_t child = parent * 2 + 1;

compare com;

while (child < _con.size())

{

if (child + 1 < _con.size() && com(_con[child] , _con[child + 1]))

{

++child;

}

if(com(_con[parent], _con[child]))

{

swap(_con[child], _con[parent]);

parent = child;

child = parent * 2 + 1;

}

else

{

break;

}

}

}

void pop()

{

swap(_con[0], _con[_con.size() - 1]);

_con.pop_back();

AdjustDown(0);

}

const T& top()

{

return _con[0];

}

size_t size() const

{

return _con.size();

}

bool empty() const

{

return _con.empty();

}

private:

Container _con;

};

}