目录

<li>关键字unsigned和signed
• • 数据在计算机中的存储
  • 原码 与 补码的转化与硬件关系
  • 原,反,补的原理:
  • 整型存储的本质
  • 变量存取的过程
  • 类型目前的作用
  • 十进制与二进制快速转换
  • 大小端字节序
  • 判断当前机器的字节序
  • "负零"(-128)的理解
  • 截断
  • 建议在无符号类型的数值后带上u,

关键字unsigned和signed

数据在计算机中的存储

• 任何数据在计算机中都必须被转化成二进制,因为计算机只认识二进制.而计算机还要区分数据是正数还是负数,则二进制又分为<code>符号位 + 数据位.li>
• 计算机内存储的整型必须是补码
• 无符号数和正数的原反补码相等,直接存入计算机中.负数需要将原码转化成补码再存储
• 类型决定了如何解释空间内部保存的二进制序列
• 浮点数默认是double类型,如果想要float需要在数后加上f,如float f = 1.1f;

原码 与 补码的转化与硬件关系

例: int b = -20; //20 = 16+4 = 2^4^ (10000)~2~+ 2^2^(100)~2~

//有符号数且负数 原码转成补码:

1000 0000 0000 0000 0000 0000 0001 0100 原码

1111 1111 1111 1111 1111 1111 1111 1011 反码 = 原码取反

1111 1111 1111 1111 1111 1111 1111 1100 补码 = 反码+1

//补码转原码

方法一: 原理

1111 1111 1111 1111 1111 1111 1111 1100 补码

1111 1111 1111 1111 1111 1111 1111 1011 反码 = 补码-1

1000 0000 0000 0000 0000 0000 0001 0100 原码 = 反码取反

方法二: 计算机硬件使用的方式, 可以使用一条硬件电路,完成原码补码互转

1111 1111 1111 1111 1111 1111 1111 1100 补码

1000 0000 0000 0000 0000 0000 0000 0011 补码取反

1000 0000 0000 0000 0000 0000 0000 0100 +1

原理:补码 = 模-原码 <=> 原码 = 模-补码 <=> 补码取反+1

原,反,补的原理:

原反补的概念从时钟引入, 8点+2 = 10点. 而8点-10也等于10点.即2是-10以12为模的补码.

-10要转化成2 ,可以用模-10来得到,但硬件中位数是固定的,模数为1000...,最高位会溢出舍弃.即全0.无法做差.

引入反码转换计算:即2 == 模-10 == 模-1+1-10 == 1111... -10 +1 == 反码+1; 这个111...-10就是反码,即反码+1==补码的由来

在二进制中,全1减任何数都是直接去掉对应的1.所以反码就是原码符号位不变,其余位全部取反

转换成补码后,底层就不需要再考虑符号位,等运算完后再看符号位.

整型存储的本质

定义unsigned int b = -10; 能否正确运行? 答案是可以的.

定义的过程是开辟空间,而空间只能存储二进制,并不关心数据的内容

数据要存储到空间里,必须先转成二进制补码.而在写入空间时,数据已经转化成补码

变量存取的过程

• 存: 字面数据必须先转成补码,再放入空间中.符号位只看数据本身是否携带+-号,和变量是否有符号无关.
• 取: 取数据一定要先看变量本身类型,然后才决定要不要看最高符号位.如果不需要,则直接将二进制转成十进制.如果需要,则需要转成原码,然后才能识别(还需要考虑最高符号位在哪里,考虑大小端)

类型目前的作用

1. 存数据前决定开辟多大的空间
2. 读数据时如何解释二进制数据

特定数据类型能表示多少个数据,取决于自己所有比特位排列组合的个数

十进制与二进制快速转换

(前置知识:需要熟记2^0到2^10的十进制结果)

1 -> 2^0

10 -> 2^1

100 -> 2^2

1000 -> 2^3 //1后面跟3个比特位就是2^3

规律: 1后n个0就是2^n,即n等于几1后面就跟几个0 --- 十进制转二进制

反过来就是1后面跟几个0,就是2的几次方 --- 二进制转十进制

因此:2^9 -> 10 0000 0000 // n

例: 67 = 64+2+1 -> 2^6+2^1+2^0 -> 1000000 + 10 + 1

= 0000 0000 .... 0100 0011

同理,二进制转十进制逆过程即可

大小端字节序

现象: vs的内存窗口中,地址从上到下依次增大,从左到右也依次增大

1. 大端:按照字节为单位,低权值位数据存储在高地址处,就叫做大端
2. 小段:按照字节为单位,低权值位数据存储在低地址处,就叫做小端(小小小)

(基本上以小端为主,大端比较少(网络))

大小端存储方案,本质是数据和空间按照字节为单位的一种映射关系

(考虑大小端问题是1字节以上的类型.short,int,double...)

判断当前机器的字节序

• 方法1: 对int a = 1 取首地址,然后(char*)&a,得到的值是1则为小端,否则为大端
• 方法2: 打开内存窗口查看地址与数据的字节序

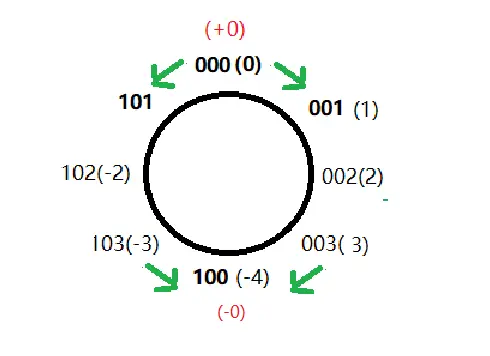
"负零"(-128)的理解

(负零的概念并不存在,只是碰巧相像)

-128实际存入到计算机中是以 1 1000 0000 表示的(计组运算器).但空间只有8位,发生截断,因此得到1000 0000.

而[1111 1111,1000 0001]~[0000 0000,0111 1111]

即[-127,-1]~[0,127] 自然数都已经被使用 .

计算机不能浪费每一个空间(最小的成本尽可能解决大量的计算),自然1000 0000也需要有相应的意义. 因此赋予数值为-128.

因为截断后也不可能恢复,所以这是一种半计算半规定的做法.

截断

截断是空间不足以存放数据时,将高位截断.

截断的是高位还是低位? 因为赋值永远都是从低地址赋起(从低到高依次赋值),因此空间不足时高位直接丢弃.

注意：表达式计算时进位产生的溢出不是截断,进位是会保存在相关寄存器中的.只有将结果保存在变量时,因为溢出,放不下,只能舍弃一部分数据,此时才发生截断.

1 0000 0001 0100

1 1111 1110 1100

0 0000 0000 1010

1 1111 1111 0110

1 0000 0000 1010

建议在无符号类型的数值后带上u,

默认的数值是有符号的,在数值后加u更加严格,可读性更好,<code>unsigned int a = 10u;