MATLAB知识点:矩阵的重构和重新排列
数学建模学习交流 2024-07-10 08:35:01 阅读 67
讲解视频:可以在bilibili搜索《MATLAB教程新手入门篇——数学建模清风主讲》。
MATLAB教程新手入门篇(数学建模清风主讲,适合零基础同学观看)_哔哩哔哩_bilibili
节选自第3章 3.3.5 矩阵的重构和重新排列
这一小节将介绍一些和矩阵的重构或重新排列相关的函数,下表给出了本小节要学的函数的名称和作用:
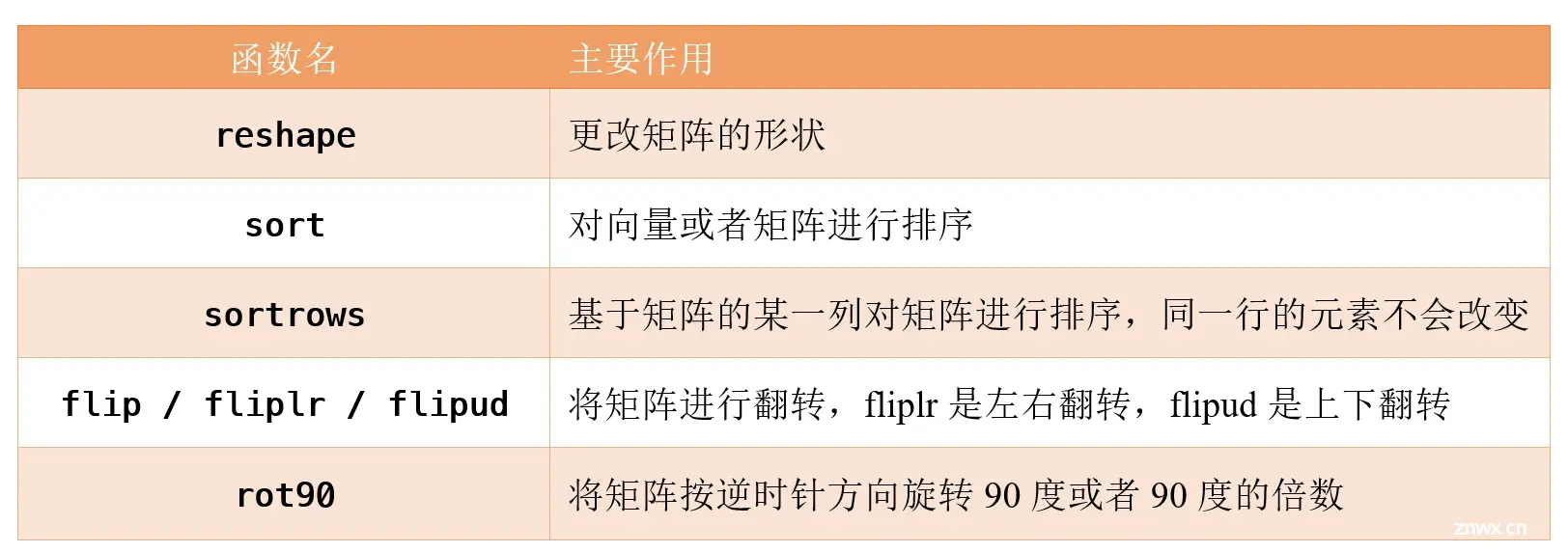
(1)reshape函数
reshape函数可以改变矩阵的形状,其常用语法为reshape(A, m, n)或者reshape(A,[m,n]),这可以将矩阵A的形状更改为m行n列,前提是转换前后的两个矩阵的元素总数要相同。
例如有一个矩阵A,它原来的形状是2行6列,如果我们需要将其形状变成3行4列,就可以使用命令:reshape(A, 3, 4).

从上面的运行结果可以看出, reshape函数实际上是按矩阵的线性索引来重新组织矩阵元素的。也就是说,它先取矩阵A的第一列,然后是第二列,依此类推,再按新的维度重新组织这些元素。因此,转换后的B矩阵中的元素和A矩阵中的元素是完全相同的,即A(:)和B(:)的结果完全相同。
另外,我们不需要自己来计算转换后的矩阵有多少行或多少列。可以只给出转换后的行数,列数用空向量[ ]代替;或者只给出转换后的列数,行数用空向量[ ]代替。MATLAB会自动帮我们计算转换后的矩阵大小。例如:若A是一个由12个元素组成的矩阵,命令reshape(A,3,[ ])、reshape(A,[ ],4)可以实现和reshape(A,3,4)一样的效果。
如果你给出的转换后的行数和列数的乘积不等于原始矩阵中元素的个数,那么MATLAB就会报错:

(2)sort函数
sort函数是用于对向量或矩阵进行排序的。如果输入的参数是矩阵的话,还可以对矩阵的每一行或每一列分别进行排序。
①对向量排序
我们先来学习sort函数对向量排序,假设v是一个向量,有下面两种基础的用法:
sort(v) 可以将向量v按照从小到大的顺序进行升序排列;
sort(v, 'descend' )可以将向量v按照从大到小的顺序进行降序排列。
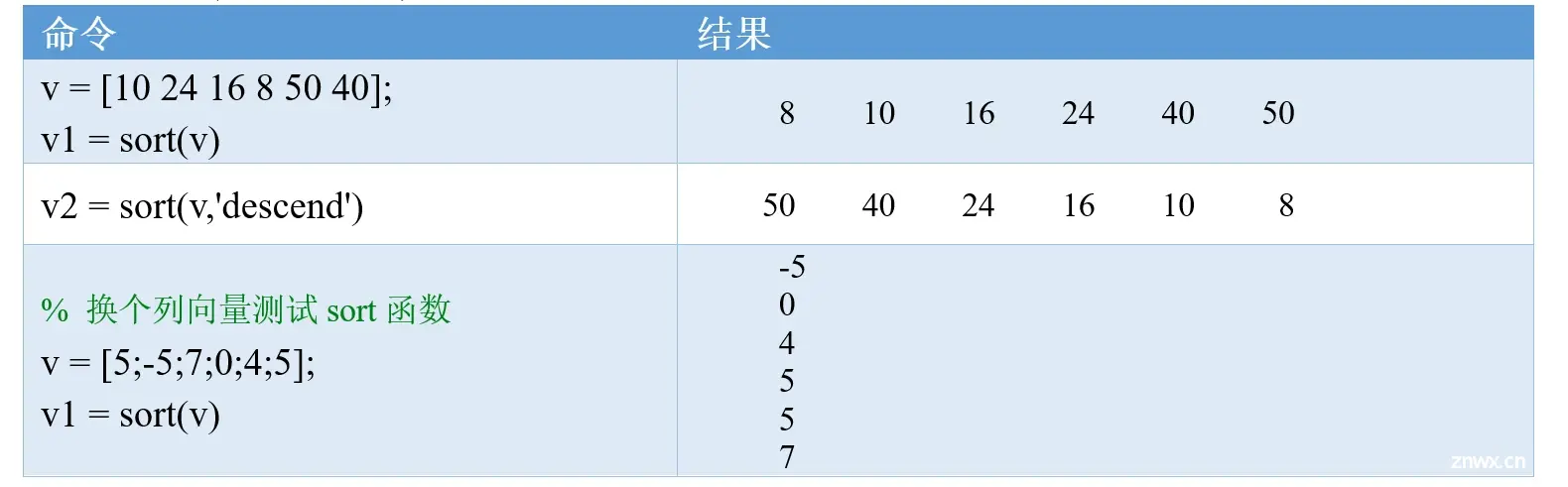
注意,上面的用法中,sort函数只有一个返回值,即排序后的向量;事实上,sort函数可以有两个返回值,基本用法为:[sort_v, ind] = sort(v)。这里,sort_v是排序后的向量,ind是排序后的向量(即sort_v)中的每个元素在原向量(即v)中的索引(即下标、位置)。我们来看一个具体的例子:

在上面的例子中,我们让sort函数返回了两个变量;sort_v和ind。它们是两个长度相等的向量,向量的方向和sort函数中输入的v向量的方向一致,都是行向量。向量v中所有元素的最小值为8,而8在v中的索引是4,因此sort_v中第一个元素为8,ind的第一个元素为4; 向量v中第二小的值为10,而10是v中的第1个元素,因此sort_v中第二个元素为10,ind的第二个元素为1;依次类推,可以得到sort_v和ind向量的值。事实上,这里有一个恒等关系成立:v(ind)运行的结果和sort_v的结果完全一样,大家可以自行验证。
下面我们看一个具体的应用场景。假设清风班上有10名同学,序号分别是1号、2号一直到10号。已知这10名同学的成绩构成的向量为:[84 70 61 90 69 78 88 74 92 76],问:清风班上哪三名同学的分数最高,分数分别是多少?

根据MATLAB返回的结果可以看出:9号、4号和7号这三名同学的分数排名前三,分别是92、90和88分。
上面这个问题比较简单,我们再来提一个问题:我们能不能知道这10名同学在班上的排名?例如:1号同学84分,在班上排名第4;2号同学70分,在班上排名第8;3号同学61分,排名第10;4号同学90分,排名第2;…… ;依此类推,最终我们想要得到的排名为:[4 8 10 2 9 5 3 7 1 6].
大家观察ind的值和我们想得到的排名的值,应该可以发现如下规律:1号同学排名第4,而ind中等于1的元素的索引也为4;2号同学排名第8,而ind中等于2的元素的索引也为8;3号同学排名第10,而ind中等于3的元素的索引也为10;4号同学排名第2,而ind中等于4的元素的索引也为2,依次类推,我们可以根据ind得到想要的排名。
根据上面的分析,我们可以将ind这个向量按照从小到大的顺序排列,排序后的向量是[1,2,3,…,10],且排序后的向量中的每个元素在向量ind中的索引就是我们要得到的排名!
因此,我们只需要加下面这行代码,new_ind就是我们想要计算的排名:
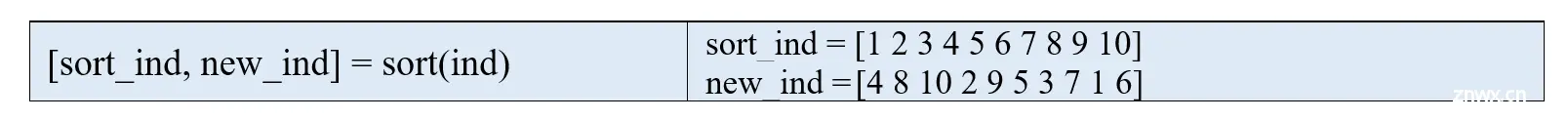
注意:如果存在同学的成绩相同的情况,那么这个代码就会存在问题,要想解决这个问题可以用到我们本章后面要学的ismember函数,这个问题也将放到本章最后的练习题中。
② 对矩阵排序
上面介绍的是sort函数对向量进行排序的应用,下面我们再来介绍sort函数对矩阵A进行排序的用法:sort(A, dim).
dim = 1时,沿着行方向(从上至下)对矩阵的每一列升序排列
dim = 2时,沿着列方向(从左至右)对矩阵的每一行升序排列
注意:(1)当dim=1时,sort(A,1)可以直接写成sort(A);(2)默认是升序排列的,我们可以在最后面加一个输入参数'descend',变成从大到小的降序排列;(3)可以有两个返回值,代表的含义和对向量排序类似,表示排序后的元素在原矩阵所在行或所在列中的索引。

(3)sortrows函数
sortrows函数可以基于矩阵的某一列对矩阵进行排序,排序后得到的新矩阵的同一行元素不会改变。这个函数的用法较多,下面我们直接用一个具体的实例来讲解它的主要用法。
假设清风老师有6名学生,下面这个矩阵保存着这六名同学在四门科目上的成绩。矩阵的每一行代表一名学生。这六名同学的四门科目的成绩对应着四列,例如第一名同学的第一科成绩为95,第二科成绩为80,依此类推。
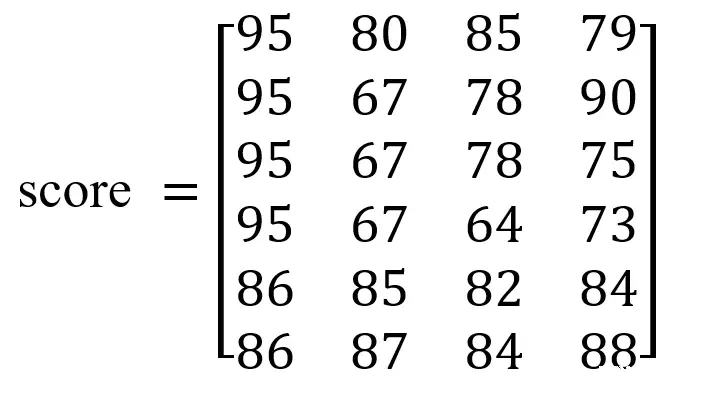
请解决下面的问题:
(1) 请基于第一科的成绩按升序对这六名同学进行排序,得到排序后的成绩矩阵。若第一科成绩相同,则基于第二科成绩升序排列。如果第二科成绩还相同,就基于第三科成绩进行排序,依此类推。

(2) 请基于第一科的成绩按升序对这六名同学进行排序。当第一科成绩相同时,请保持其在矩阵中出现的先后顺序。

(3) 请基于第二科的成绩按升序对这六名同学进行排序。当第二科成绩相同时,请保持其在矩阵中出现的先后顺序。

(4) 请基于第一科的成绩按升序对这六名同学进行排序。当第一科成绩相同时,基于第三科成绩升序排列。如果第一科和第三科都相同,就保持在矩阵中出现的先后顺序。

事实上,sortrows(score)等价于sortrows(score, 1:size(score,2)),即sortrows(score, [1,2,3,4]).
(5) 请基于第一科的成绩对这六名同学进行降序排列。当第一科成绩相同时,基于第三科成绩降序排列。如果第一科和第三科都相同,就保持在矩阵中出现的先后顺序。

(6) 请基于第一科的成绩对这六名同学进行降序排列。当第一科成绩相同时,基于第三科成绩升序排列。如果第一科和第三科都相同,就保持在矩阵中出现的先后顺序。

(7) 请基于第一科的成绩按升序对这六名同学进行排序。当第一科成绩相同时,请保持其在矩阵中出现的先后顺序,并返回索引值。

通过上面的例子可以看出,sortrows函数和sort函数的区别在于:sort函数会对矩阵的每一列分别进行排序;而sortrows函数是基于某一列进行排序的,排序后得到的新矩阵的同一行元素不会改变。
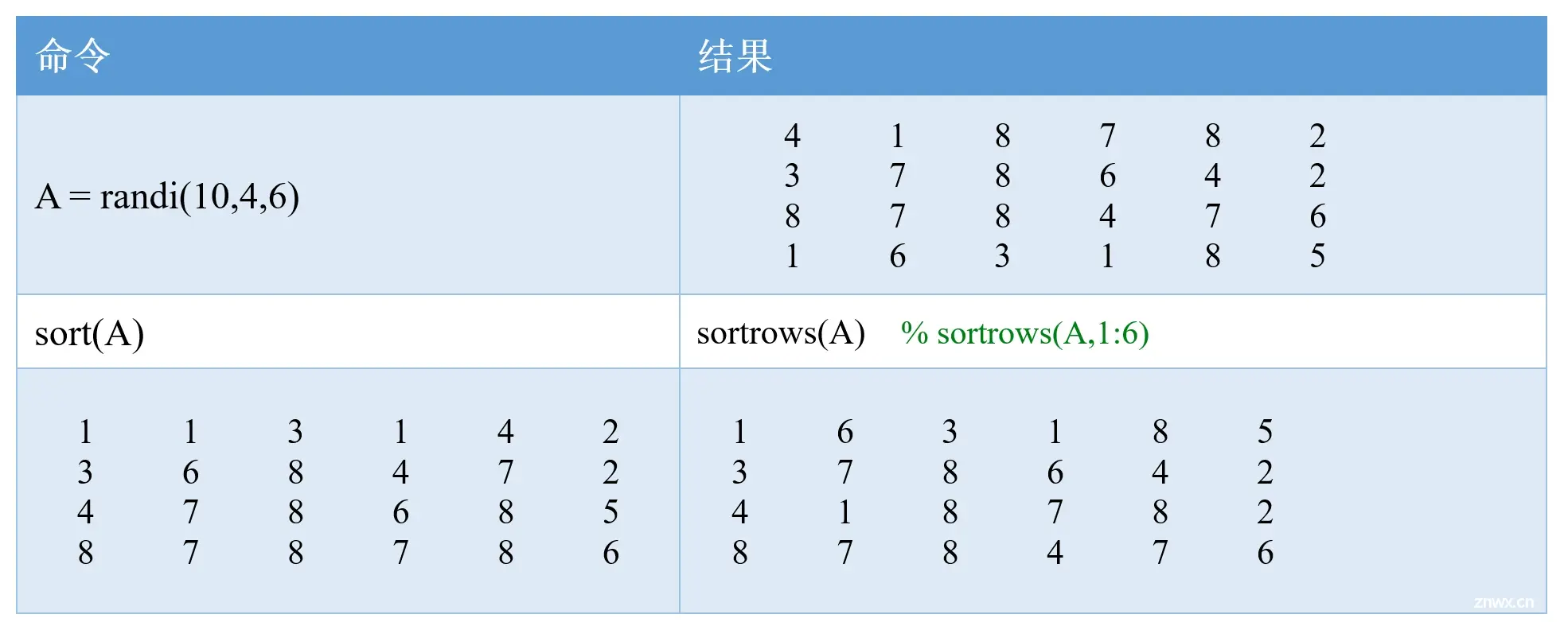
在实际的应用场景中,sort函数通常只用于对向量进行排序;如果是对矩阵或者表格数据进行排序,我们一般使用sortrows函数。如果大家熟悉Excel的话,就会发现Excel中对数据的排序就和sortrows函数类似。在以后的章节中,我们会专门讲解MATLAB中的表格数据类型,到时候还会用到sortrows函数。
以下是sortrows函数的常用用法的总结:
(1) sortrows(A)基于矩阵A中第一列元素的值按升序对矩阵进行排序。当第一列包含重复值时,sortrows会根据下一列中的值进行升序,并对后续的重复值重复此行为。另外,sortrows(A)等价于sortrows(A, 1:size(A,2)).
(2) sortrows(A,column)基于向量column中指定的列对矩阵A进行排序。例如,sortrows(A,2)会基于第二列中的元素按升序对矩阵A进行排序,如果第二列中有相同的元素,则保持其在矩阵中出现的先后顺序。sortrows(A,[2 3])首先基于第二列中的元素升序,若第二列元素相同,再基于第三列中的元素,对A矩阵进行升序排序。如果第三列也出现数值相同的情况,就保持其在矩阵中出现的先后顺序。
(3) 排序时可以指定每一列的排序方向,sortrows(___,direction)按direction指定的顺序对A进行排序。direction可以是'ascend'(默认值,对于升序排序)或 'descend'(对于降序排序)。direction 也可以是元素为 'ascend' 和 'descend' 的元胞数组,例如,sortrows(A,[1 3],{'ascend', 'descend'}) 首先基于第一列按升序对A进行排序,如果第一列中有数值相同,就基于第三列按降序排序。
(4) 除了返回排序后的矩阵,还可以返回排序后的各行在原矩阵中的位置索引。例如[sorted_A, index] = sortrows(A, column),此时A(index, :)的运行结果等于sorted_A。
(4)flip / fliplr / flipud 函数
下面我们来学习flip / fliplr / flipud这三个函数,它们可以用来对向量或矩阵进行翻转操作。其中,flip函数是一个通用的翻转函数,而fliplr和flipud是其特例,分别用于从左到右和从上到下的翻转。flip翻译成中文是翻转,而fliplr函数可以拆解为filp+ 左边left + 右边right,flipud则可以拆解为flip + 上边upper + 下边down,大家可以根据英文来进行记忆。
flip函数有两种用法:
用法1: flip(A)
如果 A 为向量,flip(A) 将翻转向量中各元素的顺序,向量的方向不变。
如果 A 为矩阵,flip(A) 将对矩阵进行上下翻转。
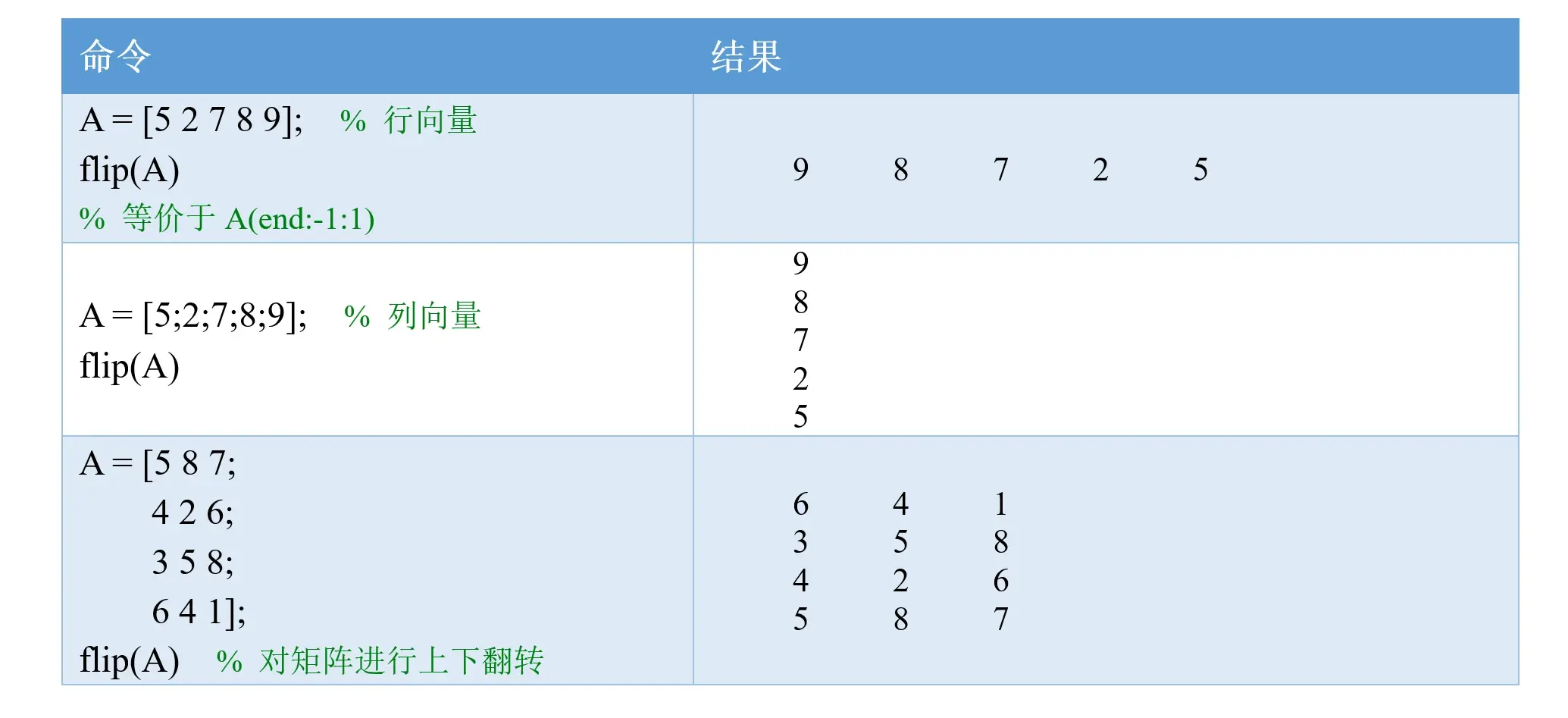
用法2: flip(A, dim)
flip(A,dim) 沿维度 dim 翻转 A 中元素的顺序。
dim为1时表示行,此时flip(A,1) 将沿着行方向对矩阵A上下翻转。
dim为2时表示列,此时flip(A,2) 将沿着列方向对矩阵A左右翻转。
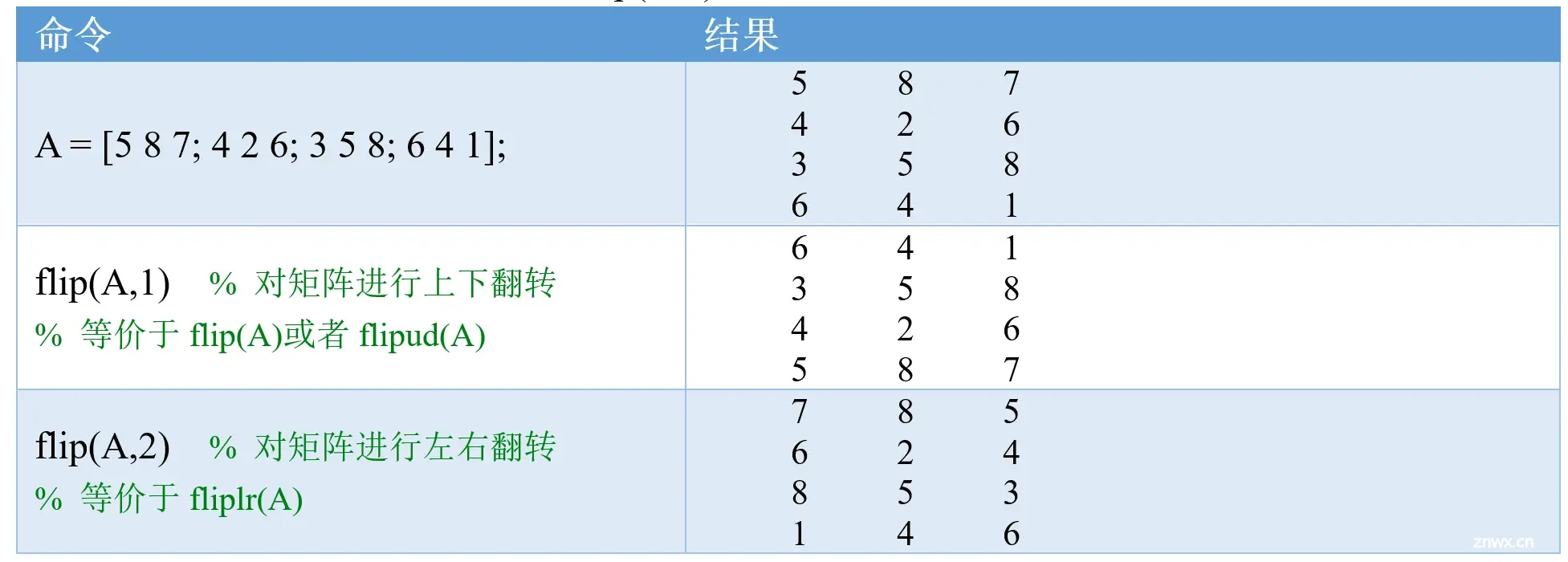
请思考:若A是一个行向量,flip(A,1)返回的结果为什么还是A?
答案:此时A被当成了一个一行的矩阵,对A进行上下翻转不会有变化。因此这提示我们,要对向量进行翻转,直接使用flip(A)即可。
flip函数用法总结:
(1) 若要对向量A中的元素进行翻转且向量的方向不变,那么可以直接使用flip(A).
(2) 若要对矩阵A进行翻转,那么flip(A)、flip(A,1)和flipud(A)都能对矩阵A进行上下翻转;flip(A,2)和fliplr(A)能对矩阵A进行左右翻转。
(5)rot90函数
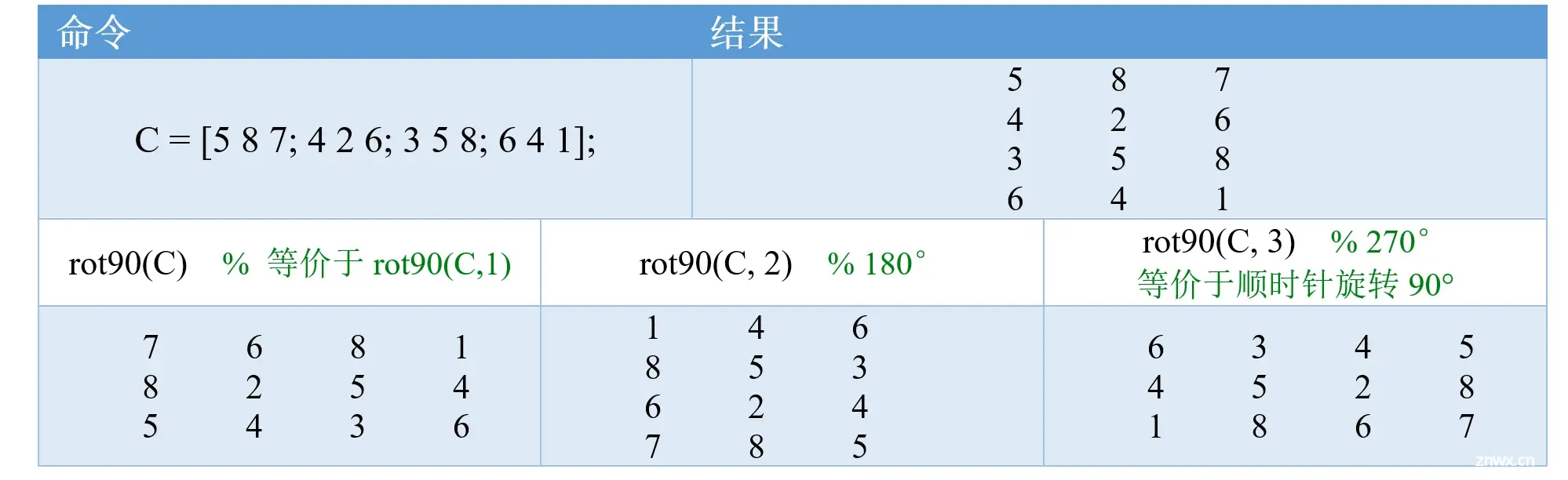
rot90函数是对矩阵进行旋转的函数,它源于英文rotate一词,中文翻译为旋转。rot90函数允许我们按90度或其倍数逆时针旋转矩阵。它的用法非常简单,rot90(A,k)将矩阵A按逆时针方向旋转k*90度,其中k是一个整数;不提供k时k默认取1。我们来看几个例子:
上一篇: 【Python】成功解决ValueError: zero-size array to reduction operation minimum which has no identity
下一篇: PySimpleGUI笔记
本文标签
声明
本文内容仅代表作者观点,或转载于其他网站,本站不以此文作为商业用途
如有涉及侵权,请联系本站进行删除
转载本站原创文章,请注明来源及作者。