🌈个人主页: 鑫宝Code

🔥热门专栏: 闲话杂谈｜ 炫酷HTML | JavaScript基础

​💫个人格言: "如无必要，勿增实体"

文章目录

独立成分分析（ICA）：解锁信号的隐秘面纱引言ICA的基本概念ICA与PCA的区别

ICA的原理ICA的算法步骤数据预处理中心化白化

独立性度量负熵Kurtosis（峰度）

ICA算法实现FastICA算法

ICA的应用音频信号分离生物医学信号处理图像处理

结论

独立成分分析（ICA）：解锁信号的隐秘面纱

引言

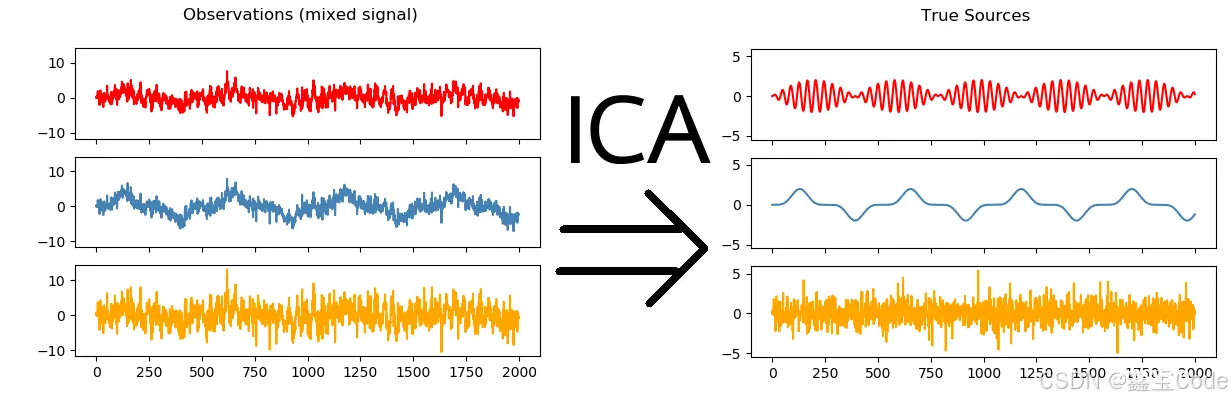
在当今数据驱动的世界中，信号处理和数据分析面临着前所未有的挑战。特别是在处理混合信号时，如何从复杂的混合体中分离出纯净的源信号，成为了研究的热点。独立成分分析（Independent Component Analysis，ICA）作为一种先进的信号处理技术，以其独特的理论基础和广泛的适用性，逐渐成为了信号分离和盲源分离领域的一颗璀璨明珠。本文旨在深入探讨ICA的原理、算法、应用及其与主成分分析（PCA）的区别，为读者提供一个全面的ICA视角。

ICA的基本概念

独立成分分析是一种统计和计算方法，用于估计和分离一组随机变量（或信号）的线性组合，即观测信号，以恢复其原本的、相互独立的源信号。ICA假设源信号是相互独立的，并且在统计上是非高斯的。这种假设使得ICA能够解决许多PCA无法解决的问题，尤其是在信号分离和盲源分离领域。

ICA与PCA的区别

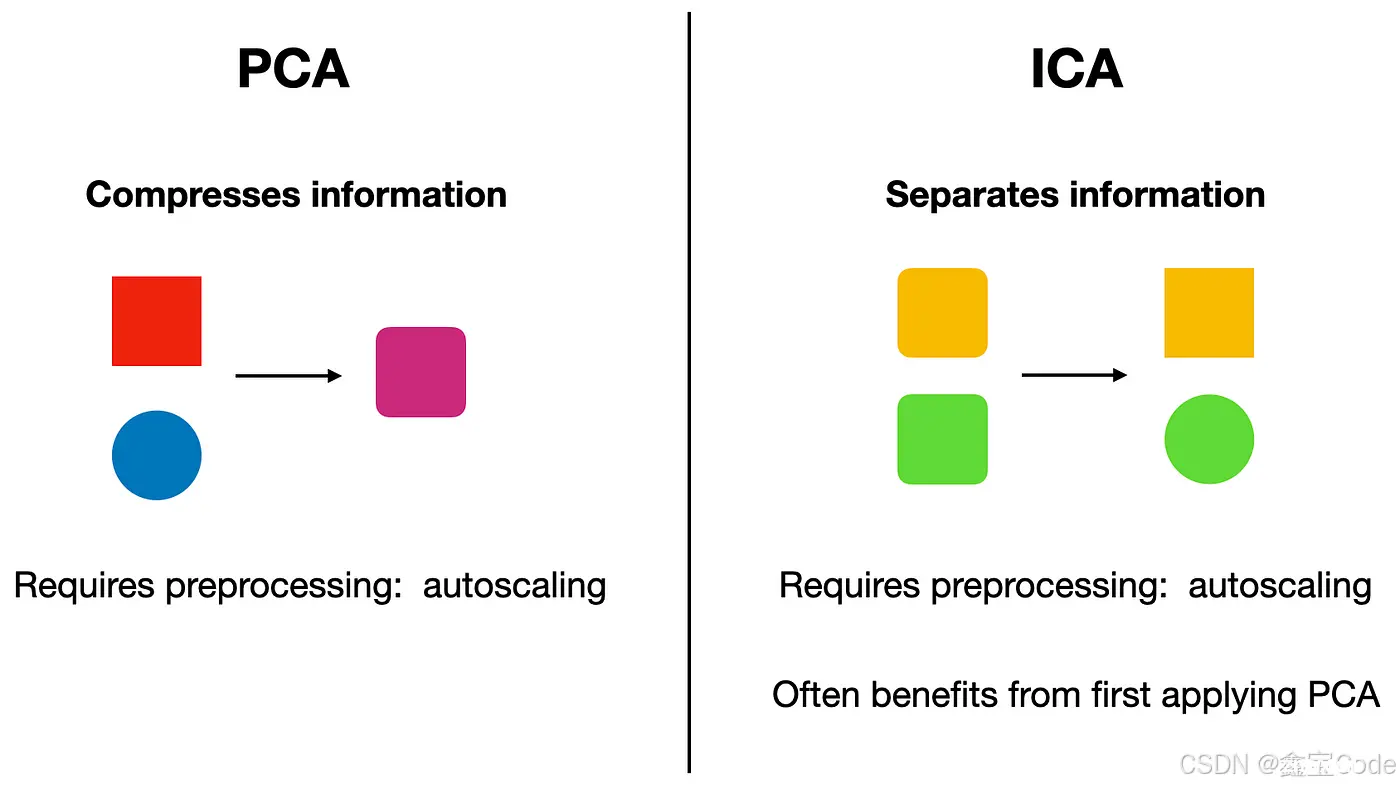
目标不同：PCA的目标是找到数据的主成分，即数据的正交基，其中第一个主成分具有最大的方差；而ICA的目标是找到源信号的独立成分，即使得输出信号的统计独立性最大化。数据假设不同：PCA假设数据服从高斯分布，而ICA则假设源信号是非高斯的，这是ICA能够成功分离信号的关键。应用领域不同：PCA广泛应用于数据降维和特征提取，而ICA主要用于信号分离和盲源分离，如音频信号分离、生物医学信号处理等。

ICA的原理

ICA的基本思想是找到一个线性变换矩阵(\mathbf{W})，使得(\mathbf{W}\mathbf{X})中的信号分量尽可能独立。这里，(\mathbf{X})是观测信号矩阵，(\mathbf{W})是ICA要估计的变换矩阵。ICA通过最大化输出信号的非高斯性或统计独立性来实现这一目标。

ICA的算法步骤

数据预处理

在ICA的算法流程中，数据预处理是至关重要的第一步，主要包括中心化和白化两个步骤。

中心化

中心化是为了消除数据的均值影响，确保数据的均值为零。设

x

\mathbf{x}

x为

N

N

N维观测信号向量，其均值为

E

[

x

]

=

μ

\mathbb{E}[\mathbf{x}] = \mathbf{\mu}

E[x]=μ，则中心化后的信号为：

x

c

=

x

−

μ

\mathbf{x_c} = \mathbf{x} - \mathbf{\mu}

xc​=x−μ

白化

白化处理的目的是去除数据间的相关性，使得数据的协方差矩阵变为单位矩阵。设

C

x

=

E

[

x

c

x

c

T

]

\mathbf{C_x} = \mathbb{E}[\mathbf{x_c}\mathbf{x_c}^T]

Cx​=E[xc​xc​T]为观测信号的协方差矩阵，白化变换可通过以下步骤完成：

计算

C

x

\mathbf{C_x}

Cx​的特征值分解：其中

U

\mathbf{U}

U是特征向量矩阵，

Λ

\mathbf{\Lambda}

Λ是特征值对角矩阵。

C

x

=

U

Λ

U

T

\mathbf{C_x} = \mathbf{U}\mathbf{\Lambda}\mathbf{U}^T

Cx​=UΛUT构造白化矩阵

W

w

h

i

t

e

n

=

U

Λ

−

1

2

U

T

\mathbf{W_{whiten}} = \mathbf{U}\mathbf{\Lambda}^{-\frac{1}{2}}\mathbf{U}^T

Wwhiten​=UΛ−21​UT应用白化矩阵，得到白化后的数据

x

w

=

W

w

h

i

t

e

n

x

c

\mathbf{x_w} = \mathbf{W_{whiten}}\mathbf{x_c}

xw​=Wwhiten​xc​

独立性度量

ICA的核心在于寻找一个变换矩阵

W

\mathbf{W}

W，使得输出信号

s

=

W

x

w

\mathbf{s} = \mathbf{W}\mathbf{x_w}

s=Wxw​的分量尽可能独立。为了度量信号的独立性，ICA采用非高斯性作为独立性的近似指标，因为独立的随机变量往往具有非高斯分布。常见的非高斯性度量包括负熵和kurtosis。

负熵

负熵

H

\mathcal{H}

H是衡量随机变量非高斯性的指标之一，定义为：

H

[

s

]

=

−

∫

p

(

s

)

log

⁡

p

(

s

)

d

s

+

const.

\mathcal{H}[s] = -\int p(s) \log p(s) ds + \text{const.}

H[s]=−∫p(s)logp(s)ds+const.

其中，

p

(

s

)

p(s)

p(s)是随机变量(s)的概率密度函数。最大化输出信号的负熵，即寻找矩阵

W

\mathbf{W}

W使得

H

[

s

]

\mathcal{H}[\mathbf{s}]

H[s]最大。

Kurtosis（峰度）

峰度是另一个常用的非高斯性度量，反映了数据分布的尖峭程度。对于随机变量(s)，其峰度定义为：

kurt

[

s

]

=

E

[

(

s

−

E

[

s

]

)

4

]

(

E

[

(

s

−

E

[

s

]

)

2

]

)

2

−

3

\text{kurt}[s] = \frac{\mathbb{E}[(s-\mathbb{E}[s])^4]}{(\mathbb{E}[(s-\mathbb{E}[s])^2])^2} - 3

kurt[s]=(E[(s−E[s])2])2E[(s−E[s])4]​−3

在ICA中，我们通常最大化绝对值的四阶矩，即：

ICA objective

=

max

⁡

W

∑

i

E

[

∣

s

i

∣

4

]

\text{ICA objective} = \max_W \sum_i \mathbb{E}[|s_i|^4]

ICA objective=Wmax​i∑​E[∣si​∣4]

ICA算法实现

ICA的算法实现通常涉及迭代优化，以最大化独立性度量。一种流行的ICA算法是FastICA，其核心是固定点迭代法，通过更新变换矩阵

W

\mathbf{W}

W，逐步逼近最优解。

FastICA算法

初始化：随机初始化

W

\mathbf{W}

W。

更新规则：对于当前的

W

\mathbf{W}

W，更新规则为：

w

n

e

w

=

x

w

g

(

W

T

x

w

)

−

β

W

x

w

\mathbf{w}_{new} = \mathbf{x_w}g(\mathbf{W}^T\mathbf{x_w}) - \beta\mathbf{W}\mathbf{x_w}

wnew​=xw​g(WTxw​)−βWxw​

其中，

g

g

g是非线性函数，

β

\beta

β是步长，通常设置为

E

[

g

(

W

T

x

w

)

2

]

\mathbb{E}[g(\mathbf{W}^T\mathbf{x_w})^2]

E[g(WTxw​)2]

正则化：为了保持

w

n

e

w

\mathbf{w}_{new}

wnew​的单位范数，需进行正则化处理：

w

n

e

w

=

w

n

e

w

∣

∣

w

n

e

w

∣

∣

\mathbf{w}_{new} = \frac{\mathbf{w}_{new}}{||\mathbf{w}_{new}||}

wnew​=∣∣wnew​∣∣wnew​​

迭代：重复步骤2和3，直至

W

\mathbf{W}

W收敛。

通过上述算法，我们最终能够获得一个变换矩阵

W

\mathbf{W}

W，使得输出信号

s

=

W

x

w

\mathbf{s} = \mathbf{W}\mathbf{x_w}

s=Wxw​的分量尽可能独立，从而实现了ICA的目标。

ICA的应用

音频信号分离

ICA在音频信号分离中有着广泛的应用，例如，它可以用来分离混在一起的多个音乐乐器的声音，或者在嘈杂环境中分离出清晰的人声。

生物医学信号处理

在脑电图（EEG）、心电图（ECG）等生物医学信号处理中，ICA能够有效分离出大脑活动的独立成分，帮助研究人员更深入地理解大脑功能和疾病机理。

图像处理

ICA在图像处理中也有所应用，比如在图像去噪、纹理分析和颜色校正等方面，通过分离出图像的不同成分，可以提高图像的质量和分析精度。

结论

独立成分分析作为一种强大的信号处理工具，以其独特的能力在信号分离和盲源分离领域展现出了巨大的潜力。通过假设源信号的独立性和非高斯性，ICA能够有效地从复杂的混合信号中恢复出纯净的源信号，为信号处理和数据分析提供了新的视角和解决方案。在未来，随着算法的不断优化和计算能力的提升，ICA将在更多的领域发挥其独特的作用，为人类理解和利用复杂信号开辟新的道路。