基于关联规则的分类算法(CBA) | 项集、频繁项集、关联规则 | arulesCBA库
梨子串桃子 2024-08-19 16:31:11 阅读 86
基于关联规则的分类算法
目前使用较多且较为简洁的关联规则分类算法是基于关联规则的分类算法(Classification Based on Association, CBA),下面将从该算法的相关概念开始介绍。
这部分笔记参考论文:孙菡悦.基于多因素交互效应的农村贫困家庭精准识别研究[D]. 华东师范大学, 2022.
示例和解释参考ChatGPT。
项集、频繁项集、关联规则
以一个小型的交易数据集为例:
| 交易ID (Transaction ID) | 购买的商品 (Items) |
|---|---|
| 1 | 牛奶, 面包, 黄油 |
| 2 | 面包, 黄油, 啤酒 |
| 3 | 牛奶, 面包, 可乐 |
| 4 | 牛奶, 面包, 黄油, 啤酒 |
| 5 | 面包, 可乐 |
项集 (Itemsets)
在这个数据集中,项集可以是不同商品的组合。我们可以从单个商品(单项集)开始,逐步扩展到多个商品的组合(多项集)。
单项集(1-itemset):{牛奶}、{面包}、{黄油}、{啤酒}、{可乐}二项集(2-itemset):{牛奶, 面包}、{牛奶, 黄油}、{面包, 黄油}、{面包, 啤酒} 等等三项集(3-itemset):{牛奶, 面包, 黄油}、{面包, 黄油, 啤酒} 等等
频繁项集 (Frequent Itemsets)
频繁项集是指在交易数据中出现频率较高的项集。我们可以设定一个最小支持度阈值,比如 60%(即项集至少出现在60%的交易中)。
支持度 (Support) 的计算方法是项集出现的次数除以总交易次数。例如,项集 {牛奶, 面包} 出现了3次(交易ID 1, 3, 4),总交易次数为5次,所以支持度为 3/5 = 60%。
根据上述数据集,频繁项集可能包括:
{牛奶, 面包},支持度 = 3/5 = 60%{面包, 黄油},支持度 = 3/5 = 60%{面包},支持度 = 5/5 = 100%
如果关联规则$ A \Rightarrow B$在发生频率不小于预先设定阈值的基础上同时符合最小置信度要求,则进一步定义该关联规则为强关联规则。
关联规则 (Association Rules)
从频繁项集中,我们可以生成关联规则,表示商品之间的关系。关联规则的形式为$ A \Rightarrow B$,表示如果购买了商品 A,则很可能会购买商品 B。关联规则有两个重要指标:
支持度 (Support):规则中项集的出现频率。例如,规则 {牛奶} -> {面包} 的支持度为 3/5 = 60%。置信度 (Confidence):表示在包含前件的交易中也包含后件的交易比例。例如,规则 {牛奶} -> {面包} 的置信度为包含 {牛奶} 的交易中同时包含 {面包} 的比例。在包含 {牛奶} 的3笔交易(交易ID 1, 3, 4)中,有3笔同时包含 {面包},所以置信度为 3/3 = 100%。该规则的置信度定义为在事件 A 发生的条件下,事件 B 发生的概率,用公式表示为:
c
o
n
f
i
d
e
n
c
e
(
A
⇒
B
)
=
P
(
B
∣
A
)
=
s
u
p
p
(
A
∪
B
)
s
u
p
p
(
A
)
confidence(A\Rightarrow B)=P(B|A)=\frac{supp(A\cup B)}{supp(A)}
confidence(A⇒B)=P(B∣A)=supp(A)supp(A∪B)
基于频繁项集,我们可以得出一些关联规则:
{牛奶} -> {面包}
支持度:3/5 = 60%置信度:3/3 = 100% {面包} -> {黄油}
支持度:3/5 = 60%置信度:3/5 = 60% {黄油} -> {面包}
支持度:3/5 = 60%置信度:3/3 = 100%
Apriori算法
生成候选项集(Candidate Generation):
通过连接频繁项集生成候选项集。频繁项集的连接是通过对频繁项集中的项进行组合来完成的。例如,从频繁1项集生成候选2项集。 剪枝(Pruning):
利用Apriori性质:如果一个项集是频繁的,那么它的所有子集也是频繁的;如果一个项集是非频繁的,那么它的所有超集也是非频繁的。因此,可以在候选项集中删除那些包含非频繁子集的项集,从而减少计算量。 计算支持度(Support Counting):
通过扫描交易数据库,计算每个候选项集的支持度。保留支持度不小于最小支持度阈值的候选项集,作为频繁项集。 重复上述步骤:
从频繁k项集生成频繁(k+1)项集,直到无法生成更多的频繁项集为止。
假设有如下交易数据集,最小支持度阈值为50%(即支持度 ≥ 0.5):
| 交易ID | 购买的商品 |
|---|---|
| T1 | {A, B, C} |
| T2 | {A, C} |
| T3 | {A, B, D} |
| T4 | {B, C} |
| T5 | {A, B, C, D} |
步骤1:生成频繁1项集
L
1
L1
L1
扫描交易数据库,计算每个单项的支持度:
{A}: 4/5 = 0.8{B}: 4/5 = 0.8{C}: 4/5 = 0.8{D}: 2/5 = 0.4
支持度不小于0.5的项集为频繁项集:
L
1
=
{
{
A
}
,
{
B
}
,
{
C
}
}
L1 = \{ \{A\}, \{B\}, \{C\} \}
L1={ { A},{ B},{ C}}
步骤2:生成候选2项集
C
2
C2
C2
对频繁1项集进行连接:
C
2
=
{
{
A
,
B
}
,
{
A
,
C
}
,
{
B
,
C
}
}
C2 = \{ \{A, B\}, \{A, C\}, \{B, C\} \}
C2={ { A,B},{ A,C},{ B,C}}
计算候选2项集的支持度:
{A, B}: 3/5 = 0.6{A, C}: 3/5 = 0.6{B, C}: 3/5 = 0.6
支持度不小于0.5的项集为频繁项集:
L
2
=
{
{
A
,
B
}
,
{
A
,
C
}
,
{
B
,
C
}
}
L2 = \{ \{A, B\}, \{A, C\}, \{B, C\} \}
L2={ { A,B},{ A,C},{ B,C}}
步骤3:生成候选3项集
C
3
C3
C3
对频繁2项集进行连接:
C
3
=
{
A
,
B
,
C
}
C3={\{A,B,C}\}
C3={ A,B,C}
计算候选3项集的支持度:
{A, B, C}: 2/5 = 0.4
支持度小于0.5,故没有频繁3项集:
L
3
=
∅
L3=∅
L3=∅
至此,算法终止,得到的频繁项集为:
L
=
{
L
1
,
L
2
}
=
{
{
{
A
}
,
{
B
}
,
{
C
}
}
}
,
{
{
A
,
B
}
,
{
A
,
C
}
,
{
B
,
C
}
}
L=\{L1,L2\}={\{\{ \{A\}, \{B\}, \{C\} \}\},\{ \{A, B\}, \{A, C\}, \{B, C\} \}}
L={ L1,L2}={ { { A},{ B},{ C}}},{ { A,B},{ A,C},{ B,C}}
步骤4:关联规则生成
从频繁2项集中生成关联规则,并计算每条规则的置信度:
规则 {A} -> {B}
支持度:3/5 = 0.6置信度:3/4 = 0.75 规则 {B} -> {A}
支持度:3/5 = 0.6置信度:3/4 = 0.75 规则 {A} -> {C}
支持度:3/5 = 0.6置信度:3/4 = 0.75 规则 {C} -> {A}
支持度:3/5 = 0.6置信度:3/4 = 0.75 规则 {B} -> {C}
支持度:3/5 = 0.6置信度:3/4 = 0.75 规则 {C} -> {B}
支持度:3/5 = 0.6置信度:3/4 = 0.75
arulesCBA库的简单使用
这里参考arulesCBA官方文档:https://cran.r-project.org/web/packages/arulesCBA/arulesCBA.pdf,解释参考ChatGPT。
将连续特征离散化
由于CBA算法要求数据类型为离散型,arulesCBA封装好了离散化的函数,若需要根据实际问题采用其他算法,可参考上文引用的论文。
<code>discretizeDF.supervised函数实现了几种有监督的方法,将连续变量转换为适用于关联规则挖掘和构建关联分类器的分类变量。
加载iris数据集并输出描述性统计结果:
data("iris")
summary(iris)
输出以下信息:

使用Species的监督离散化:
<code>iris.disc <- discretizeDF.supervised(Species ~ ., iris)
summary(iris.disc)
attributes(iris.disc$Sepal.Length) # 检查特定特征的属性
输出以下信息:

以<code>Sepal.Length:为例,被划分为三个区间 [-Inf,5.55), [5.55,6.15), [6.15, Inf],每个区间的样本数量分别是59, 36, 和 55。
也可以对指定的特征进行离散化:
iris.disc2 <- discretizeDF.supervised(Species ~ Sepal.Length + Sepal.Width, iris)
使用前面离散规则对样本进行离散化:
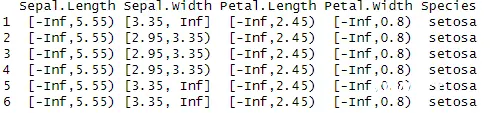
discretizeDF(head(iris), methods = iris.disc)
这个命令使用之前通过discretizeDF.supervised()函数生成的离散化方法(iris.disc)对iris数据集的前六个样本进行离散化,输出以下信息:
挖掘iris数据集的关联规则
导入库:<code>library(arulesCBA)
创建分类器:classifier <- CBA(Species ~ ., data = iris, supp = 0.05, conf = 0.9)
第一个参数:Species是目标变量,而.表示使用数据集中除Species以外的所有变量作为特征。
**第二个参数:**指定用于训练分类器的数据集是iris数据集。
**第三个参数:**设置支持度的阈值,即规则在数据集中出现的最小比例。支持度是衡量某个模式在数据集中出现频率的指标。这里设置为5%,即某个规则至少需要在5%的数据中出现才会被考虑。
**第四个参数:**设置置信度的阈值,即规则在预测目标变量时的可靠性程度。置信度是指规则的前件和后件同时出现的比例,通常用于评估规则的准确性。这里设置为90%,意味着我们希望规则在90%的情况下是正确的。
运行后会输出以下信息:
CBA Classifier Object
Formula: Species ~ .
Number of rules: 8
Default Class: versicolor
Classification method: first
Description: CBA algorithm (Liu et al., 1998)
Formula: Species ~ .
这是指分类器使用的公式。Species是目标变量,即分类器要预测的类别。.表示使用数据集中除目标变量之外的所有特征来进行预测。在这个例子中,目标变量是鸢尾花的品种(Species),而特征包括花瓣长度、花瓣宽度、萼片长度和萼片宽度等属性。
Number of rules: 8
这是分类器生成的关联规则的数量。CBA算法根据训练数据生成规则,每个规则用于将输入数据映射到一个类别。在这个例子中,算法生成了8条规则。
Default Class: versicolor
当输入数据不符合任何规则时,分类器将预测为默认类别。在这个例子中,默认类别是versicolor,这意味着如果没有规则匹配,分类器将预测鸢尾花的品种为versicolor。
Classification method: first
这是分类器选择规则的方法。first表示分类器在预测时会使用匹配的第一条规则。这意味着分类器会按照规则的顺序进行匹配,一旦找到匹配的规则,就会使用该规则进行预测,而不会考虑其他规则。
Description: CBA algorithm (Liu et al., 1998)
这是对所使用的算法的描述,指出这个分类器使用的是CBA算法,这是由Liu等人于1998年提出的基于关联规则的分类算法。
查看生成的关联规则:inspect(classifier$rules)
运行后会输出以下信息:

lhs (左侧项)
这些是规则的前件(条件),即规则适用的前提条件。例如,规则1中,<code>{Petal.Length=[-Inf,2.45)}表示当花瓣长度在该范围内时,规则适用。
rhs (右侧项)
这些是规则的后件(结论),即在满足前件条件时,预测的类别。例如,规则1中,{Species=setosa}表示如果条件成立,则预测品种为setosa。
support (支持度)
规则适用的数据点在整个数据集中所占的比例。例如,规则1的支持度为0.3333333,表示该规则适用于33.33%的数据。
confidence (置信度)
规则的准确性,即在前件条件满足时,后件也为真的比例。例如,规则1的置信度为1.0,表示在所有花瓣长度在[-Inf,2.45)范围内的数据中,品种都是setosa。
coverage (覆盖率)
前件条件在整个数据集中出现的比例。例如,规则1的覆盖率为0.3333333,表示花瓣长度在[-Inf,2.45)范围内的数据占总数据的33.33%。
lift (提升度)
规则相对于随机猜测的优势。例如,提升度为3表示该规则比随机猜测提高了三倍的正确率。
count (计数)
满足该规则的实际数据点的数量。例如,规则1有50个数据点符合条件。
size (规则项数)
规则中的条件数。例如,规则1中有2个条件。
coveredTransactions (覆盖的事务数)
满足前件条件的事务数,即数据点数量。
totalErrors (总错误数)
规则预测错误的次数。
把剪枝后的关联规则导出:
pruned_rules_df <- as(classifier$rules, "data.frame")
write.csv(pruned_rules_df , file = "pruned_rules_subset.csv", row.names = FALSE)
使用训练好的分类器对前六个样本进行预测:predict(classifier, head(iris))
输出混淆矩阵:table(pred = predict(classifier, iris), true = iris$Species)
输出的混淆矩阵如下:

Rows (pred)
代表分类器的预测类别。
Columns (true)
代表数据的真实类别。
Cells
数值表示分类器在预测中正确和错误的次数。
转换成事务格式:
<code>iris_trans <- prepareTransactions(Species ~ ., iris, disc.method = "mdlp")
iris_trans
输出以下信息:

使用<code>mdlp(Minimum Description Length Principle)方法对连续变量进行离散化,输出显示数据集有150个事务(行)和15个项目(列)。每个事务对应一个数据点,每个项目对应一个离散化后的特征值。
verbose = TRUE:启用详细输出,显示训练过程中的详细信息:classifier <- CBA(Species ~ ., data = iris_trans, supp = 0.05, conf = 0.9, verbose = TRUE)
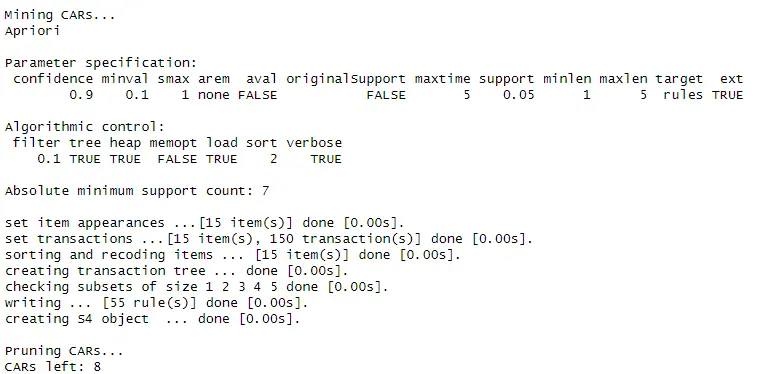
Apriori:使用Apriori算法来挖掘关联规则。Parameter specification:列出了参数设置,包括最小置信度、最小支持度等。Algorithmic control:控制算法的具体实现参数,如过滤器、排序等。Absolute minimum support count: 7:绝对最小支持度计数,即规则至少应满足7个数据点。Apriori过程:显示了挖掘规则的具体步骤,包括设置项出现、事务、排序和重编码、创建事务树等。最终生成了55条规则。剪枝:<code>CARs left: 8修剪后剩余8条规则。修剪是删除冗余或不可靠规则的过程,以提高分类器的效率和准确性。
上面的函数挖掘的是后项为目标变量的关联规则,如果不要求后项为目标变量,可以使用以下函数:
rules <- apriori(iris, parameter = list(supp = 0.05, conf = 0.9))
rules_df <- as(rules, "data.frame")
write.csv(rules_df, file = "rules.csv", row.names = FALSE)
以返贫数据集演示完整代码
这里以返贫数据集为例,下载数据集可直接运行代码出结果。不过用 apriori 挖掘关联规则,产生的关联规则有100多万条,csv文件有400多M,所以不放进仓库了。代码、数据集、结果以及笔记见Gitee仓库:
https://gitee.com/chuantaoli/data_mining_and_courses_learning/tree/master/CBA%E7%AE%97%E6%B3%95
# 导入库和数据
library(arulesCBA)
library(readxl)
excel_file <- "D:/贫困论文/总数据集.xlsx"
data <- read_excel(excel_file)
# 数据离散化
summary(data)
vars_to_discretize <- setdiff(names(data), c("性别", "学历","劳动技能","健康状况", "是否参加城乡居民基本医疗保险",
"是否参加城乡居民基本养老保险", "是否享受人身意外保险补贴", "就业渠道",
"是否有龙头企业带动", "主要燃料类型","是否有创业致富带头人带动",
"是否有卫生厕所", "入户路类型", "是否通生产用电",
"是否加入农民专业合作组织"))
data_to_discretize <- data[ , vars_to_discretize]
data_to_discretize$`风险是否已消除` <- as.factor(data_to_discretize$`风险是否已消除`)
data_to_discretize_disc <- discretizeDF.supervised(`风险是否已消除` ~ ., data_to_discretize, disc.method = "mdlp")
summary(data_to_discretize_disc)
# 将离散化后的特征与不离散化的特征合并
non_discretized_vars <- data[ , c("性别", "学历","劳动技能","健康状况", "是否参加城乡居民基本医疗保险",
"是否参加城乡居民基本养老保险", "是否享受人身意外保险补贴", "就业渠道",
"是否有龙头企业带动", "主要燃料类型","是否有创业致富带头人带动",
"是否有卫生厕所", "入户路类型", "是否通生产用电",
"是否加入农民专业合作组织")]
data_final <- cbind(data_to_discretize_disc, non_discretized_vars)
summary(data_final)
# CBA函数挖掘关联规则,后项为因变量
classifier <- CBA(`风险是否已消除` ~ ., data = data_final, supp = 0.01, conf = 0.7)
inspect(classifier$rules)
# 导出关联规则
pruned_rules_df <- as(classifier$rules, "data.frame")
write.csv(pruned_rules_df , file = "pruned_rules_subset.csv", row.names = FALSE)
## 如果不能运行,就转化成事务格式
# data_final[] <- lapply(data_final, as.factor)
# str(data_final)
# data_final_trans <- as(data_final, "transactions")
# apriori挖掘关联规则,后项是任何特征
rules <- apriori(data_final, parameter = list(supp = 0.09, conf = 0.9))
rules_df <- as(rules, "data.frame")
write.csv(rules_df, file = "rules.csv", row.names = FALSE)
_rules_df , file = "pruned_rules_subset.csv", row.names = FALSE)
## 如果不能运行,就转化成事务格式
# data_final[] <- lapply(data_final, as.factor)
# str(data_final)
# data_final_trans <- as(data_final, "transactions")
# apriori挖掘关联规则,后项是任何特征
rules <- apriori(data_final, parameter = list(supp = 0.09, conf = 0.9))
rules_df <- as(rules, "data.frame")
write.csv(rules_df, file = "rules.csv", row.names = FALSE)
本文标签
声明
本文内容仅代表作者观点,或转载于其他网站,本站不以此文作为商业用途
如有涉及侵权,请联系本站进行删除
转载本站原创文章,请注明来源及作者。