在许多情况下，机器学习模型比传统线性模型更受欢迎，因为它们具有更好的预测性能和处理复杂非线性数据的能力。然而，机器学习模型的一个常见问题是它们缺乏可解释性。

例如，集成方法如XGBoost和随机森林将许多个体学习器的结果组合起来生成结果。尽管这通常会带来更好的性能，但它使得难以知道数据集中每个特征对输出的贡献。

为了解决这个问题，可解释人工智能（explainable AI, xAI）被提出并越来越受欢迎。xAI领域旨在解释这些不可解释的模型（所谓的黑匣子模型）如何进行预测，实现最佳的预测准确性和可解释性。这样做的动机在于，许多机器学习的真实应用场景不仅需要良好的预测性能，还要解释生成结果的方式。

例如，在医疗领域，可能会根据模型做出的决策而失去或挽救生命，因此了解决策的驱动因素非常重要。此外，能够识别重要变量对于识别机制或治疗途径也很有帮助。最受欢迎、最有效的xAI技术之一是SHAP。

文章源码及数据，想实战的可以按照如下方式获取

技术交流

独学而无优则孤陋而寡闻，技术要学会交流、分享，不建议闭门造车。

技术交流与答疑、源码获取，均可加交流群获取，群友已超过2000人，添加时最好的备注方式为：来源+兴趣方向，方便找到志同道合的朋友。

方式①、微信搜索公众号：Python学习与数据挖掘，后台回复：资料

方式②、添加微信号：dkl88194，备注：资料

资料1

资料2

我们打造了《数据分析实战案例宝典》，特点：从0到1轻松学习，方法论及原理、代码、案例应有尽有，所有案例都是按照这样的节奏进行表述。

1. 介绍

SHAP概念由Lundberg & Lee于2017年提出，但实际上是基于早在此之前存在的博弈论<code>Shapley值。

简而言之，SHAP值通过计算每个特征的边际贡献来工作，方法是在许多有和没有该特征的模型中查看（每个观察值的）预测，根据每个这些减少特征集模型中的权重计算这种贡献，然后总结所有这些实例的加权贡献。

在这里，简单地说：对于一个观察值而言，SHAP值的绝对值越大，影响预测的作用就越大。因此，对于给定特征的所有观察值的绝对SHAP值的平均值越大，该特征就越重要。

使用SHAP库在Python中实现SHAP值很容易，许多在线教程已经解释了如何实现。然而，我发现所有整合SHAP值到Python代码的指南都存在两个主要缺陷。

第一点是：大多数指南在基本的训练/测试拆分上使用SHAP值，但**不在交叉验证上使用（见图1）**

使用交叉验证可以更好地了解结果的普适性，而基本的训练/测试拆分的结果很容易受到数据划分方式的影响而发生剧烈变化。正如我在最近的“<code>营养研究中的机器学习”(https://doi.org/10.1093/advances/nmac103)文章中所解释的那样，除非你处理的数据集非常庞大，否则交叉验证几乎总是优于训练/测试拆分。

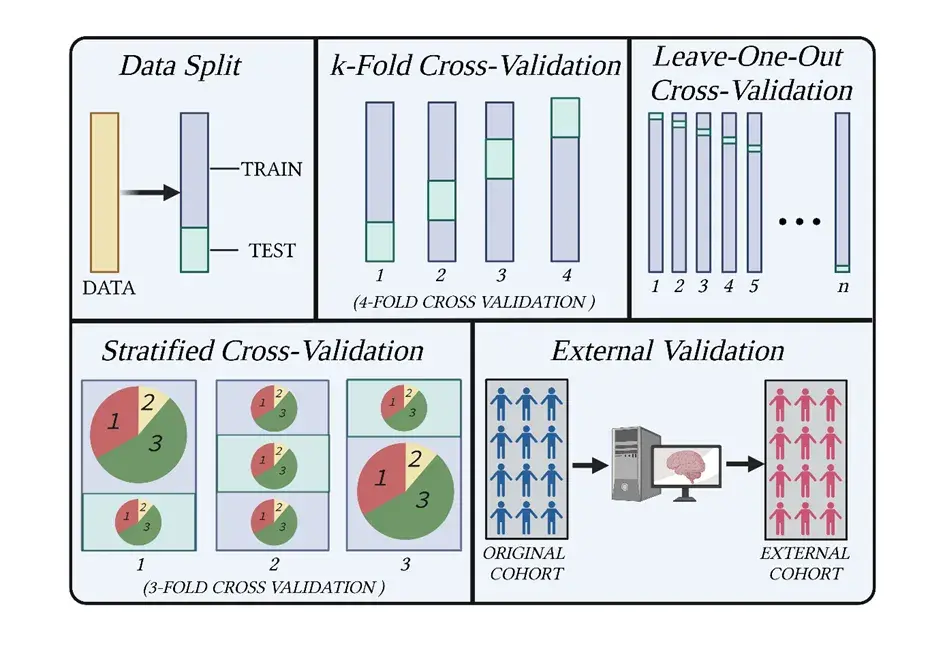
图1. 机器学习中的不同评估程序。

另一个缺点是：我遇到的所有指南都**<code>没有使用多次交叉验证来推导其SHAP值**

虽然交叉验证比简单的训练/测试拆分有很大的改进，但最好每次都使用不同的数据拆分来重复多次。特别是在数据集较小的情况下，结果可能会因数据如何拆分而大为不同。这就是为什么经常建议重复100次交叉验证以对结果有信心的原因。

为了解决这些缺点，我决定编写一些代码来实现它。本文将向您展示如何获取多次重复交叉验证的SHAP值，并结合嵌套交叉验证方案。对于我们的模型数据集，我们将使用波士顿住房数据集，并选择功能强大但不可解释的随机森林算法。

2. SHAP实践

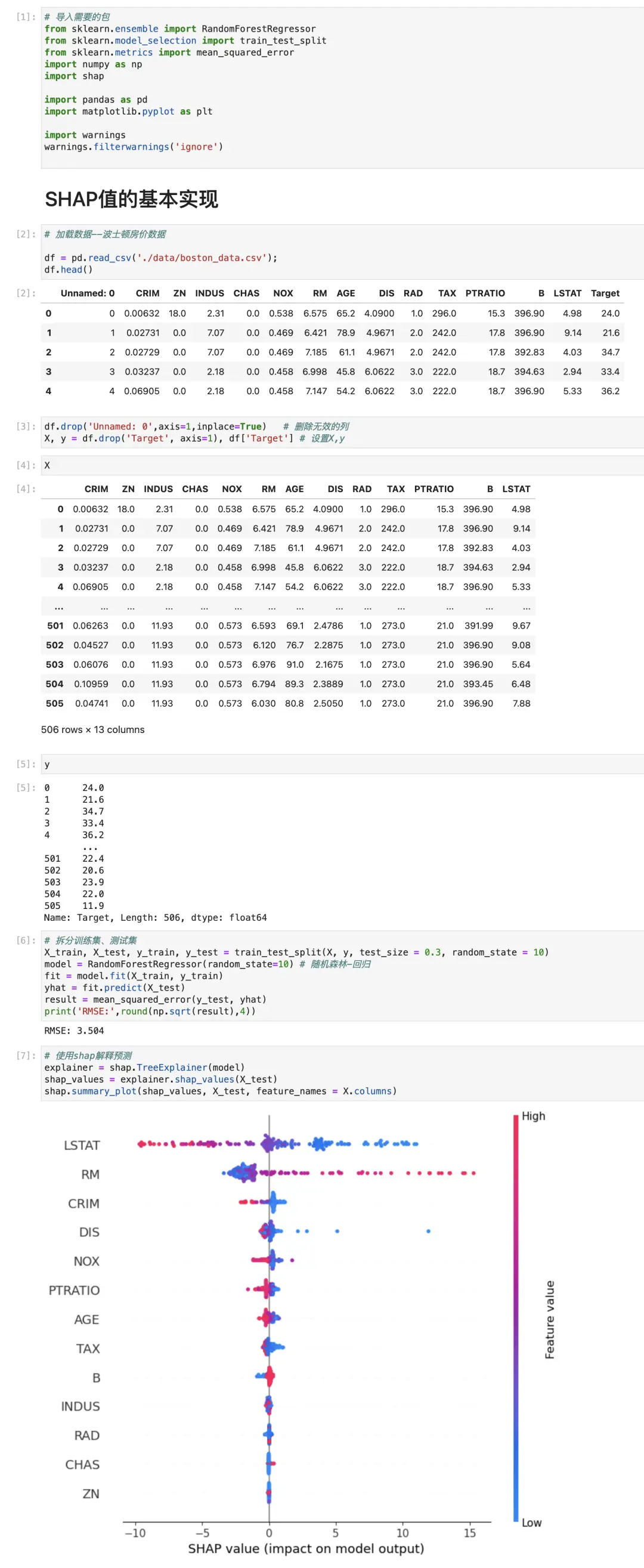
2.1. SHAP值的基本实现

无论何时，当使用各种循环构建代码时，通常最好从最内部的循环开始向外工作。试图从外部开始构建代码，按运行顺序构建代码，容易混淆且在出现问题时更难进行故障排除。

因此，我们从SHAP值的基本实现开始。

我假设您熟悉SHAP的一般用途和其实现代码的外观，因此我不会花太长时间进行说明。

我会在代码中添加注释，因此您可以检查这些注释，如果您仍然不确定，那么请查看介绍中的链接或库的文档。我还会在需要时导入库，而不是在开始时一次性导入所有库，这样有助于理解。

2.2. 将交叉验证与SHAP值相结合

我们经常使用<code>sklearn的cross_val_score或类似方法自动实现交叉验证。

但是这种方法的问题在于所有过程都在后台进行，我们无法访问每个fold中的数据。

当然，如果我们想获得所有数据点的SHAP值，则需要访问每个数据点（请记住，每个数据点在测试集中仅用一次，在训练中使用<code>k-1次）。为了解决这个问题，我们可以将KFold与.split结合使用。

通过循环遍历我们的<code>KFold对象，并使用.split方法，我们可以获取每个折叠的训练和测试索引。

在这里，折叠是一个元组，其中fold[0]是每个折叠的训练索引，fold[1]是测试索引。

现在，我们可以使用此方法从原始数据帧中自己选择训练和测试数据，从而提取所需的信息。

我们通过创建新的循环来完成此操作，获取每个折叠的训练和测试索引，然后像通常一样执行回归和 SHAP 过程。

然后，我们只需在循环外添加一个空列表来跟踪每个样本的 SHAP 值，然后在循环结束时将其添加到列表中。我使用 <code>#-#-# 来表示这些新添加的内容。

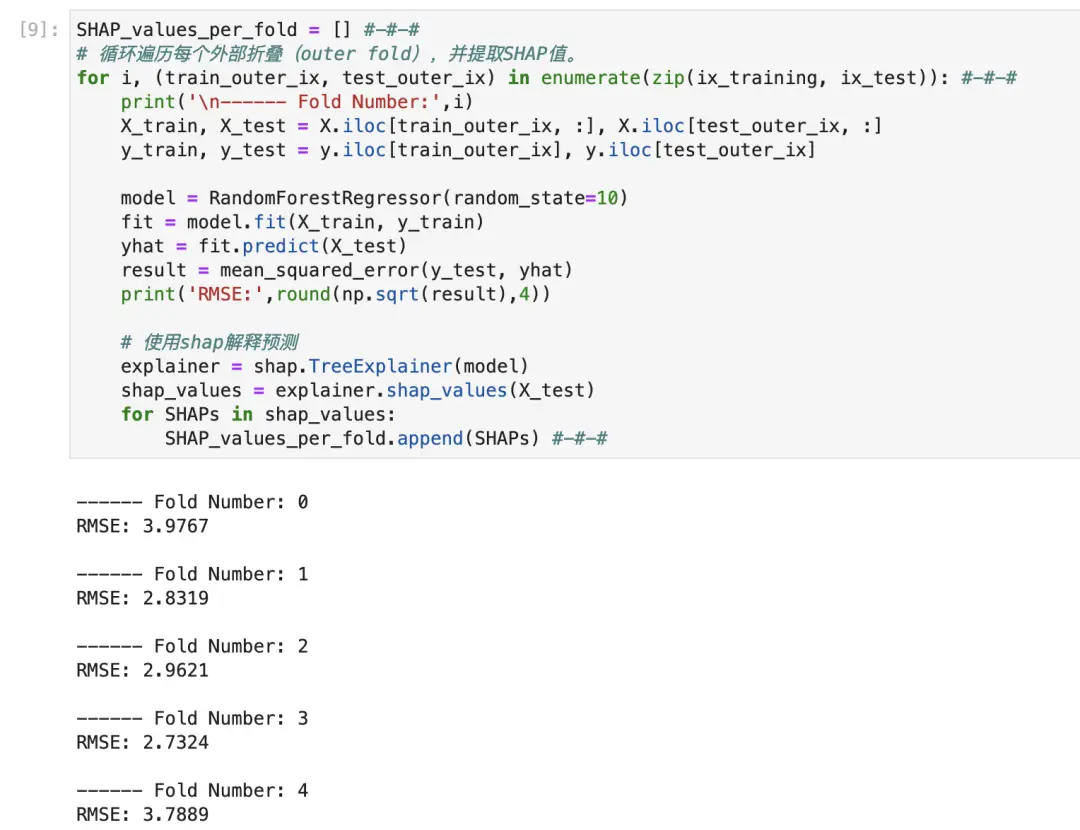
现在，我们针对每个样本都有SHAP值，而不仅仅是数据的一个测试分割样本，我们可以使用SHAP库轻松绘制这些值。

我们首先需要更新X的索引，以匹配它们出现在每个折叠的每个测试集中的顺序，否则颜色编码的特征值会全部错误。

请注意，我们在<code>summary_plot函数中重新排序X，以便我们不保存我们对原始X数据帧的更改。

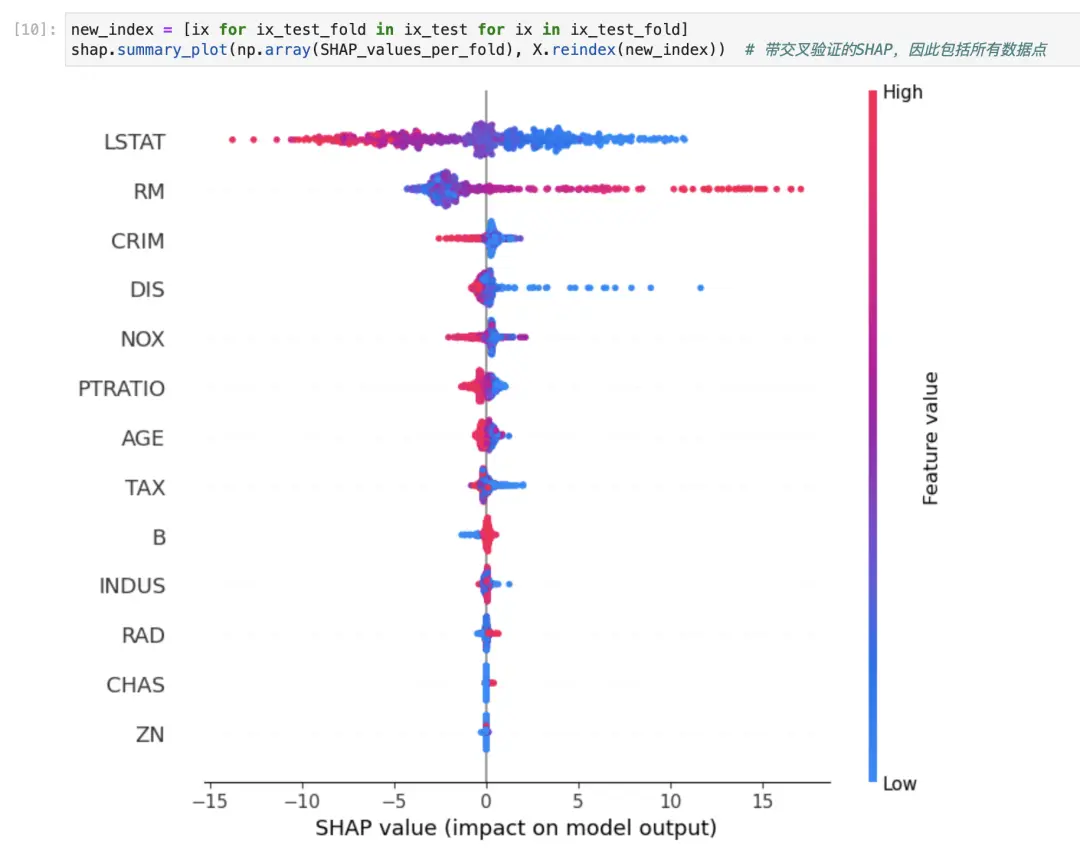
上面，是带交叉验证的SHAP，包括所有数据点，所以比之前的点密集。

从图中可以看出，与仅使用训练/测试拆分时相比，现在有更多的数据点（实际上是全部数据点）。

这样，我们的过程已经得到了改善，因为我们可以利用整个数据集而不仅仅是一部分。

但我们仍然不清楚稳定性。即，如果数据被分割得不同，结果会如何改变。

幸运的是，我们可以在下面编写代码来解决这个问题。

2.3. 重复交叉验证

使用交叉验证可以大大提高工作的鲁棒性，尤其是在数据集较小的情况下。然而，如果我们真的想做好数据科学，交叉验证应该在许多不同的数据拆分上重复执行。

首先，我们现在需要考虑的不仅仅是每个折叠的SHAP值，还需要考虑每个重复和每个折叠的SHAP值，然后将它们合并到一个图表中进行绘制。

在Python中，字典是强大的工具，这就是我们将用来跟踪每个样本在每个折叠中的SHAP值。

首先，我们决定要执行多少次交叉验证重复，并建立一个字典来存储每个重复中每个样本的SHAP值。

这是通过循环遍历数据集中的所有样本并在我们的空字典中为它们创建一个键来实现的，然后在每个样本中创建另一个键来表示交叉验证重复。

接下来，我们在现有代码中添加一些新行，使我们能够重复交叉验证过程CV_repeats次，并将每次重复的SHAP值添加到我们的字典中。

这很容易实现，只需更新代码末尾的一些行，以便我们不再将每个样本的SHAP值列表附加到列表中，而是更新字典。

注：收集每个折叠的测试分数可能也很重要，尽管我们在这里不这样做，因为重点是使用SHAP值，但这可以通过添加另一个字典轻松更新，其中CV重复是键，测试分数是值。

代码看起来像这样，其中 <code>#-#-# 表示对现有代码的更新：

为了可视化，假设我们想要检查索引号为10的样本的第五个交叉验证重复，我们只需写：

其中第一个方括号代表样本编号，第二个代表重复次数。输出是在第五次交叉验证重复后，样本编号为10的X每列的SHAP值。

要查看一个个体所有交叉验证重复的SHAP值，只需在第一个方括号中键入数字即可：

然而，这对我们来说并没有太多用处（除了故障排除目的）。我们真正需要的是绘制一个图表来可视化这些数据。

我们首先需要对每个样本的交叉验证重复进行SHAP值的平均值计算，以便绘制一个值（如果您愿意，您也可以使用中位数或其他统计数据）。取平均值很方便，但可能会隐藏数据内部的可变性，这也是我们需要了解的。因此，虽然我们正在取平均值，但我们还将获得其他统计数据，例如最小值，最大值和标准偏差：

以上代码表示：对于原始数据框中的每个样本索引，从每个 SHAP 值列表（即每个交叉验证重复）中制作数据框。该数据框将每个交叉验证重复作为行，每个 X 变量作为列。我们现在使用相应的函数和使用 axis = 1 以列为单位执行计算，对每列取平均值、标准差、最小值和最大值。然后我们将每个转换为数据框。

现在，我们只需像绘制通常的值一样绘制平均值。我们也不需要重新排序索引，因为我们从字典中取出SHAP值，它与X的顺序相同。

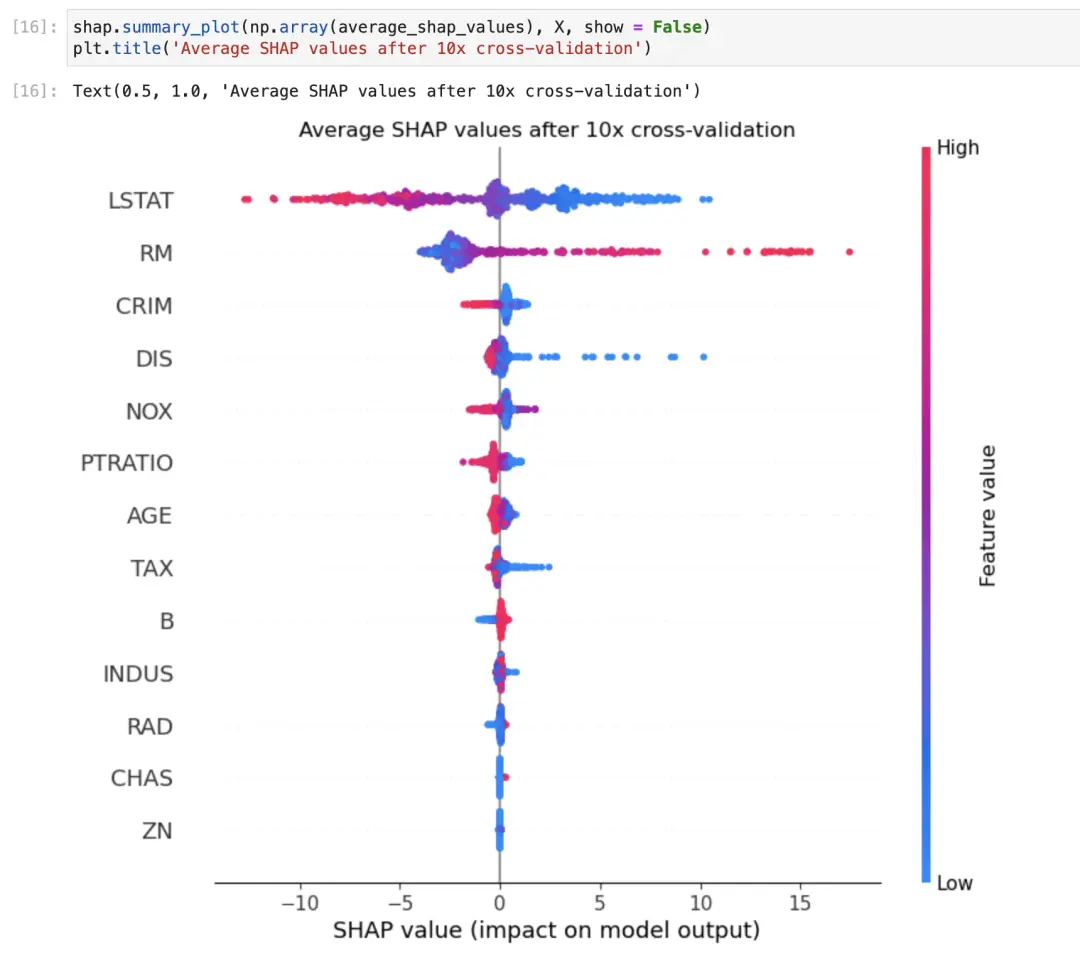
上图是重复交叉验证多次后的平均SHAP值。

由于我们的结果已经经过多次交叉验证的平均化，因此它们比仅执行一次简单的训练/测试拆分更加健壮和可信。

但是，如果您比较之前和之后的图形，并且除了额外的数据点外，几乎没有什么变化，您可能会感到失望。但是不要忘记，我们使用的是一个模型数据集，该数据集非常整洁，具有良好的特性，并且与结果具有强烈的关系。在不那么理想的情况下，像重复交叉验证这样的技术将揭示实际数据在结果和特征重要性方面的不稳定性。

如果我们想要进一步增强我们的结果（当然我们想要），我们可以添加一些图表来了解我们建议的特征重要性的变异性。这很重要，因为每个样本的平均SHAP值可能会掩盖它们在数据不同分割下的变化程度。

为了做到这一点，我们必须将我们的数据帧转换为长格式，之后我们可以使用 <code>seaborn 库来制作一个 catplot。

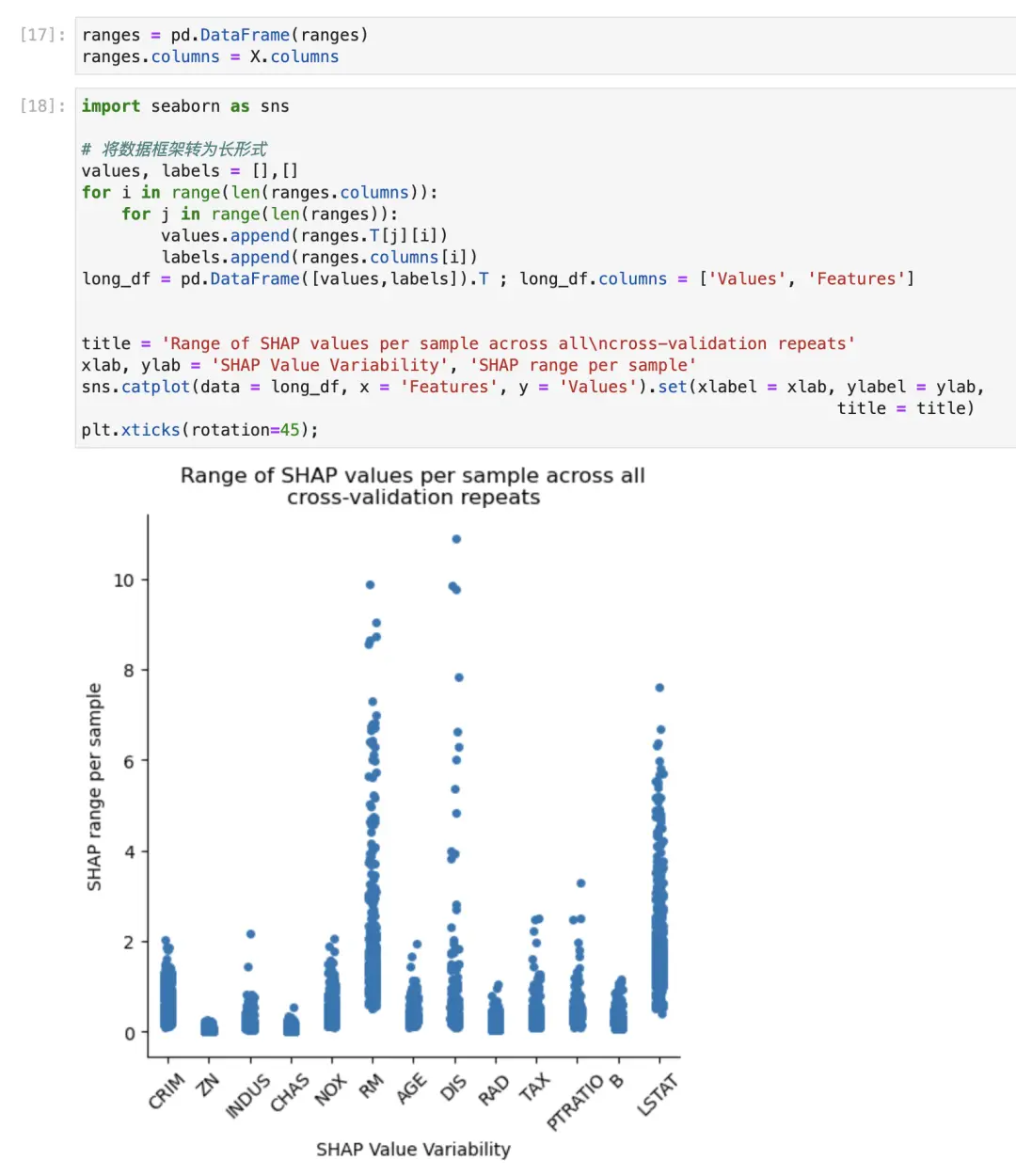
上图，我们可以看到每个样本的每次CV重复中的范围（最大值-最小值）。理想情况下，我们希望 轴上的值尽可能小，因为这意味着更一致的特征重要性。

我们应该谨记，这种可变性也对绝对特征重要性敏感，即被认为更重要的特征自然会具有更大范围的数据点。我们可以通过对数据进行缩放来部分地解决这个问题。

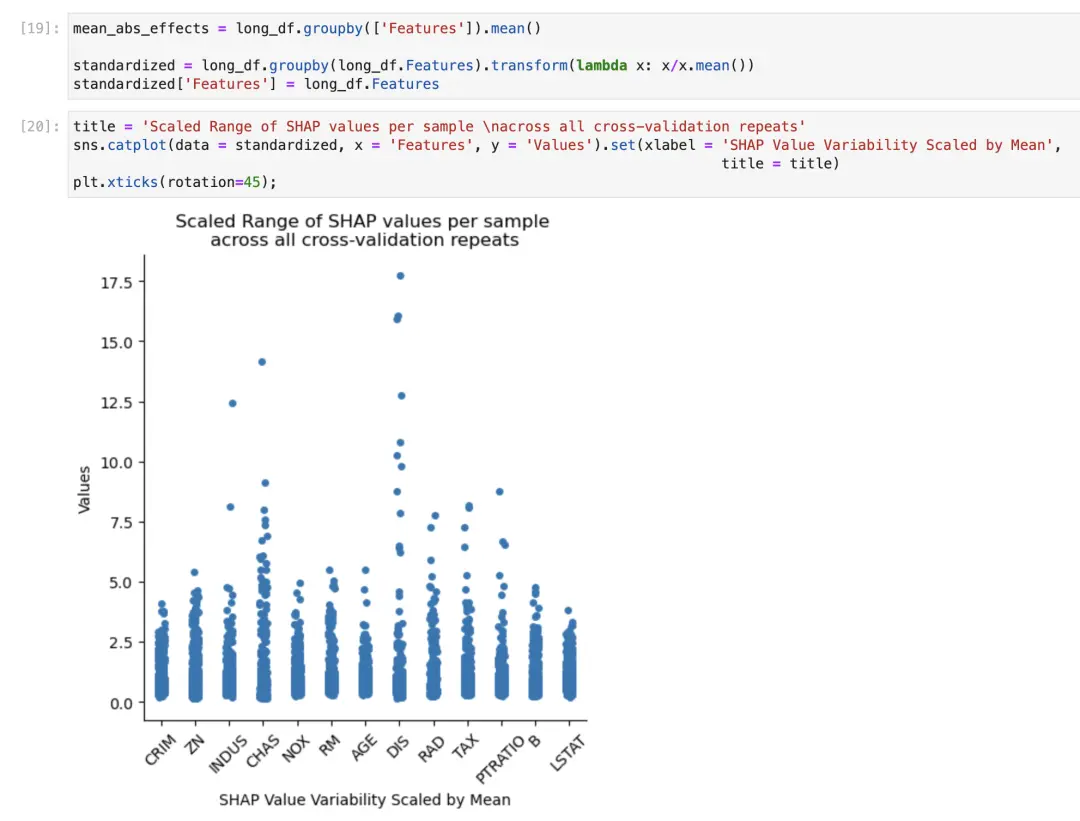
的图与 的图相似，但现在每个观测值都按每个特征的平均值缩放。

请注意LSTAT和RM这两个最重要的特征看起来有多不同。现在，我们可以更好地反映按特征的整体重要性缩放的可变性，这可能更或不更相关，具体取决于我们的研究问题。

我们可以根据我们收集的其他统计数据，例如标准差，想出类似的情节。

2.4. 嵌套交叉验证

所有这些都很好，但有一件事情缺失了：我们的随机森林是默认模式。虽然它在这个数据集上表现得很好，但在其他情况下可能不是这样。此外，为什么我们不应该尝试最大化我们的结果呢？

我们应该注意不要陷入机器学习示例中似乎很常见的陷阱，即在测试集中也存在的数据上优化模型超参数。通过简单的训练/测试拆分，我们可以轻松避免这种情况。只需在训练数据上优化超参数即可。

但是一旦交叉验证进入方程式，这个概念似乎被忘记了。实际上，人们经常使用交叉验证来优化超参数，然后使用交叉验证对模型进行评分。在这种情况下，发生了数据泄漏，我们的结果将会（即使只是稍微）过于乐观。

嵌套交叉验证是我们的解决方案。它涉及在我们正常的交叉验证方案（这里称为“外循环”）中取出每个训练折叠，并使用训练数据中的另一个交叉验证（称为“内循环”）来优化超参数。这意味着我们在训练数据上优化超参数，然后仍然可以获得有关优化模型在未见数据上表现如何的更少偏差的想法。

这个概念可能有点难以理解，但对于希望了解更多细节的人，我在上面链接的文章中进行了解释。无论如何，代码并不那么困难，阅读代码可能会有助于理解。实际上，我们在上面的过程中已经准备了大部分的代码，只需要进行一些小的调整。让我们看看它的表现。

嵌套交叉验证的主要考虑因素，特别是在我们使用许多重复时，是需要花费很多时间才能运行。因此，我们将保持参数空间较小，并使用随机搜索而不是网格搜索（尽管随机搜索通常在大多数情况下表现良好）。如果您确实想要更彻底地进行搜索，可能需要在HPC上保留一些时间。

无论如何，在我们的初始for循环之外，我们将建立参数空间：

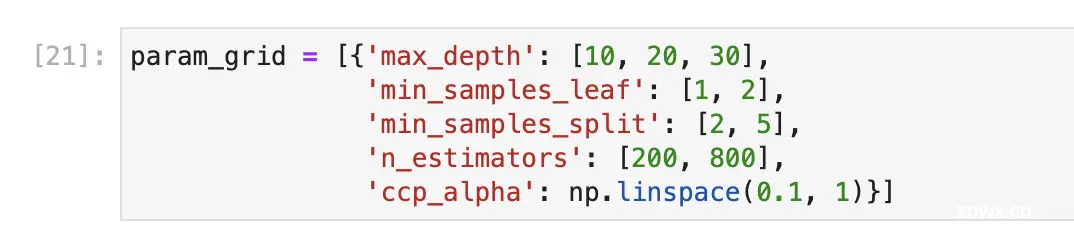
我们随后对原始代码进行以下更改：

<code>CV现在将变为cv_outer，因为我们现在有两个交叉验证，我们需要适当地引用每个交叉验证

在我们的for循环中，我们循环遍历训练和测试ID，我们添加内部交叉验证方案cv_inner

然后，我们使用RandomizedSearchCV来优化我们的模型在inner_cv上选择我们最好的模型，然后使用最佳模型从测试数据中派生SHAP值（这里的测试数据是外部折叠测试）。

就是这样。为了演示目的，我们将<code>CV_repeats减少到2，因为否则，我们可能要在这里一段时间。在实际情况下，您需要保持足够高的次数以保持稳健的结果，同时也要获得最佳参数，对于这些参数，您可能需要HPC（或耐心）。

请参见下面的代码，其中 #-#-# 表示新添加的内容。

3. 结论

能够解释复杂的AI模型变得越来越重要。

SHAP值是一种很好的方法，但是在较小的数据集中，单次训练/测试拆分的结果并不总是可信的。

通过多次重复(嵌套)交叉验证等程序，您可以增加结果的稳健性，并更好地评估如果基础数据也发生变化，结果可能会如何变化。