基于等效电路模型(RC)的锂离子电池参数在线辨识
CSDN 2024-06-14 09:31:06 阅读 68

在电池管理系统(BMS)中,等效电路模型(ECM)是模拟电池动力学的常用方法。然而,模型的简单性和准确性之间总是存在着矛盾。简单的模型通常无法反映电池的所有动态效应,这可能会给参数识别带来误差。然而,一个复杂的模型总是有太多的参数需要识别,并可能存在参数发散问题。
一、介绍
电动汽车(EV)和混合动力汽车(HEV)有望解决石油危机和传统汽车加剧的环境问题。电动汽车和混合动力汽车的关键部件是二次电池。为了满足车辆的电力需求,需要将低压电芯大量连接成电池组。完善的电池管理系统(BMS)是保证每个电池安全持久运行的关键。
二、电池模型

由上图可得等效电路数学表达式:
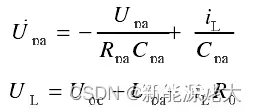
将上式离散化后可得:可得动力电池RC等效模型的离散状态方程:
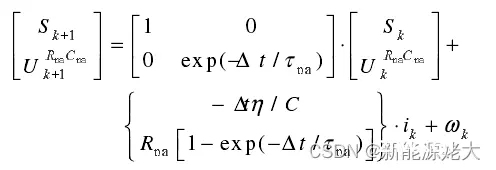
离散输出观测方程:
![]()
式中:Sk sk分别为离散状态k、k+1时刻的动力电池电荷状态;△t为采样周期;C为电池的标称容量,Ah;为库仑系数,充电时n=1,放电时n<1 ;7p=RpCp为时间常数;R0为电池欧姆内阻;Rp为RC等效电路的电池极化内阻;Ca为RC等效电路的等效电容;
三、在线参数辨识
将最上面的两个公式进行拉普拉斯变换得到:

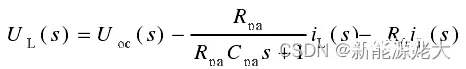
令
![]()
得到:
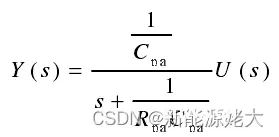
拉普拉斯变换规则,令:


离散化后得到:
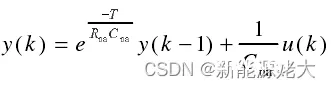
令

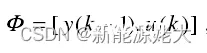
得到:
![]()
采用最小二乘法,使残差的平方和最小,即,
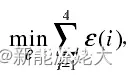
则可以得出参数θ最优估计值为
![]()
至此,即可以辨识得到参数Rpa,Cpa
四、代码实现
话不多说,直接上干货。代码如下:
%clear all;a=xlsread('C:/Users/ustc/Desktop/RLS/fe081dst');%a=xlsread('E:/test/15tem');y=a(:,2);%votage,y是矩阵a中第2列元素排成的列向量u=a(:,3);%current,u是矩阵a中第3列元素排成的列向量s=length(u);%length(u)求矩阵u的长度,若u为M*N则,测得长度为M和N中的最大值soc=a(:,4);%矩阵a中的第4列为电池的SOC,赋值给变量soc%soc(1)=0.99;%for i=1:s-1% soc(i+1)=soc(i)+u(i)/(3600*7.86);%end%y1=y(13385:13422);%u1=u(13385:13422);%s=length(y1);b(:,1)=[1 log(0.99) log(0.01) 0 u(1) 0]';%state,样本集合x=1;%forgetting factor%chushihuac(:,1)=[0.1 0.1 0.1 0.9 0 0]';%estimated needed,待辨识参数P=10000*eye(6,6);%函数eye(M,N):生成M*N的单位矩阵for i=2:s b(:,i)=[1 log(soc(i)) log(1-soc(i)) y(i-1) u(i) u(i-1)]';%样本集合 e(i)=y(i)-b(:,i)'*c(:,(i-1)); %计算偏差 K=(P*b(:,i))/(x+b(:,i)'*P*b(:,i)); P=(P-K*b(:,i)'*P)/x; c(:,i)=c(:,(i-1))+K*e(i);endfor i=1:s vol(i)=b(:,i)'*c(:,i); ocv(i)=(c(1,i)+c(2,i)*log(soc(i))+c(3,i)*log(1-soc(i)))./(1-c(4,i)); r(i)=(-c(6,i)+c(5,i))/(1+c(4,i));%欧姆内阻 k0(i)=c(1,i)/(1-c(4,i)); k1(i)=c(2,i)/(1-c(4,i));k2(i)=c(3,i)/(1-c(4,i)); ti(i)=(1+c(4,i))/(2*(1-c(4,i)));%时间常数 rps(i)=(1+2*ti(i))*c(5,i)-2*r(i)*ti(i)-r(i);%极化内阻 cps(i)=ti(i)/rps(i);%极化电容endplot(vol);hold onplot(y);plot(ocv);figure;plot(r);
五、仿真结果分析
1.电流
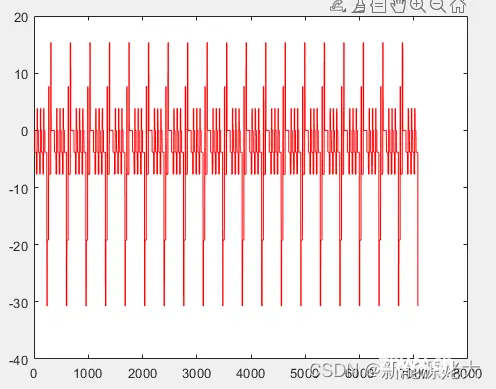
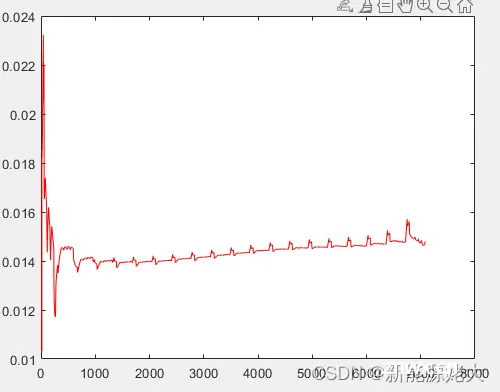
2.极化电阻Rs
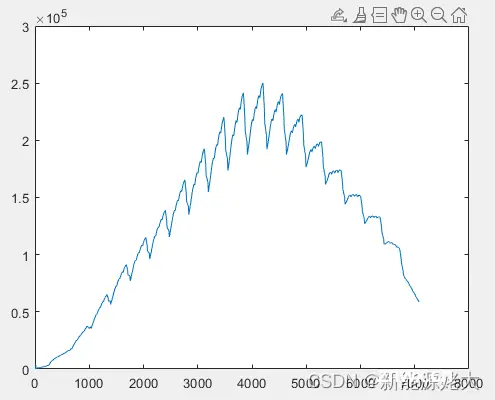
3.极化电容Rp
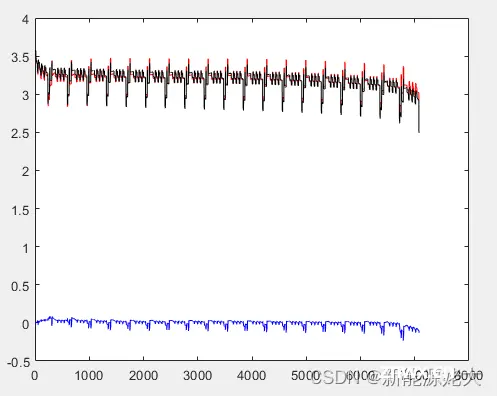
4.端电压对比图(上)及误差(下)
六、学习资料加油站
硕博期间所有的程序代码,一共2个多g,可以给你指导,赠送半个小时的语音电话答疑。电池数据+辨识程序+各种卡尔曼滤波算法都在里面了,后续还会有新模型的更新。快速入门BMS软件。某鹅:2629471989
声明
本文内容仅代表作者观点,或转载于其他网站,本站不以此文作为商业用途
如有涉及侵权,请联系本站进行删除
转载本站原创文章,请注明来源及作者。