好几个月之前学的了，当时手懒没总结，突然闲下来把笔记补上

Introduction

之前讲解了基于值函数的方法和基于策略的方法，基于值函数的方法只学习一个价值函数，而基于策略的方法只学习一个策略函数。Actor-Critic价值函数策略函数都学习。Actor-Critic 是囊括一系列算法的整体架构，Actor-Critic 算法本质上是基于策略的算法，因为这一系列算法的目标都是优化一个带参数的策略，只是会额外学习价值函数，帮助策略函数更好地学习。

回顾一下，在 REINFORCE 算法中，目标函数的梯度中有一项轨迹回报，指导策略的更新。REINFOCE 算法用蒙特卡洛方法来估计

Q

(

s

,

a

)

Q(s,a)

Q(s,a)，Actor-Critic 算法拟合一个值函数来指导策略进行学习。在策略梯度中，可以把梯度写成下面这个更加一般的形式:

REINFORCE 通过蒙特卡洛采样的方法对策略梯度的估计是无偏的，但是方差非常大。可以用形式(3)引入基线函数（baseline function）

b

(

s

t

)

b(s_t)

b(st​)来减小方差。也可以采用 Actor-Critic 算法估计一个动作价值函数

Q

Q

Q，代替蒙特卡洛采样得到的回报，便是形式(4)。可以把状态价值函数

V

V

V作为基线，从

Q

Q

Q函数减去这个

V

V

V函数则得到

A

A

A函数，我们称之为优势函数（advantage function），是形式(5)。更进一步，我们可以利用等式

Q

=

r

+

γ

V

Q=r+\gamma V

Q=r+γV得到形式(6)。围绕这几种形式讲，主要还是时序差分残差

一、Actor-Critic推导

AC就是轨迹回报用Q值拟合

二、Advantage Actor-Critic

A2C加个baseline，减小方差，让权重有正有负，使用优势函数代替Critic网络中的原始回报，可以作为衡量选取动作值和所有动作平均值好坏的指标。

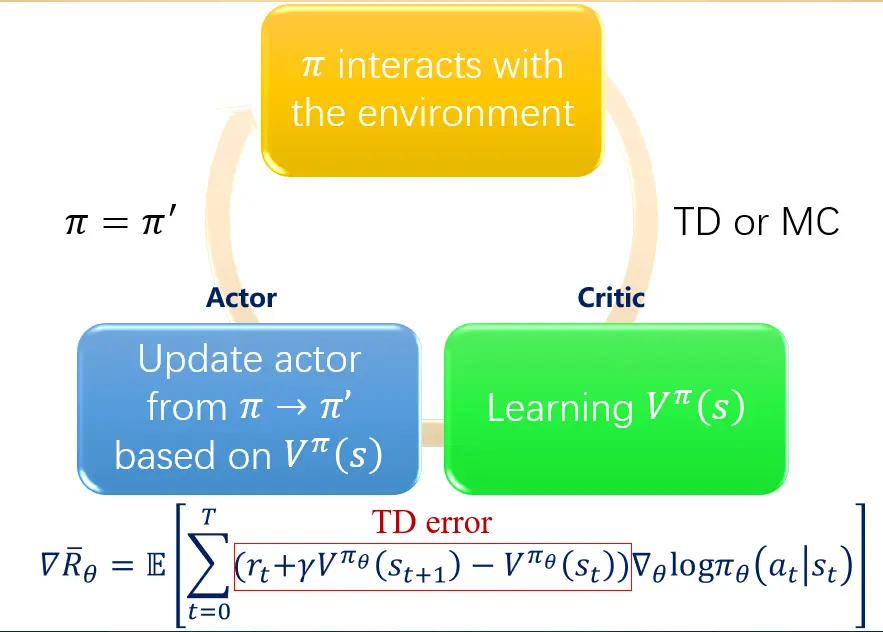
将 Actor-Critic 分为两个部分：Actor（策略网络）和 Critic（价值网络）

Actor 要做的是与环境交互，并在 Critic 价值函数的指导下用策略梯度学习一个更好的策略。Critic 通过 Actor 与环境交互收集的数据学习一个价值函数，用于评估在当前状态策略好坏，帮助 Actor 进行策略更新。

Tips：一、需要估计两个网络：V 网络和Actor的策略网络，它们前面几个层（layer）可以共享，比如输入图像前期都用一些卷积神经网络处理，把图像抽象成高级（high level）信息，对于Actor-Critic来说是可以共用的。 二、在Actor-Critic中，对 π 输出的分布设置一个约束，使分布的**熵（entropy）**不能太小，熵用于衡量策略在选择动作时的随机性程度，也就是希望不同的动作被采用的概率平均一些。可以促使策略保持一定的探索性，以便更好地探索环境并学习到更好的策略。

三、Asynchronous Advantage Actor-Critic (A3C)

一种异步梯度优化框架，神经网络与强化学习算法相结合可以让算法更有效，但稳定性较差。通常使用经验回放来去除数据的相关性，让训练更加稳定。但只适用于（off-policy）强化学习算法。A3C使用异步并行，多个（actor/worker）并行可以采取不同的策略与环境互动去除数据相关性，代替经验回放技术，这使得框架可以用于同策略方法

异步（Asynchronous）：在A3C中，会创建多个并行的环境, 有一个全局网络（global network）和多个工作智能体（worker），每个智能体都有自己的网络参数集(一开始是全局网络的副本）。并行训练，每个worker同时与自己的环境副本交互，更新主结构中的参数. 并行中的 worker 们独立、互不干扰, 而主结构的参数更新受到副结构提交更新的不连续性干扰, 所以更新的相关性被降低, 收敛性提高.

使用Hogwild!作为更新方法。Hogwild!是一种并行更新的方法，其中多个线程可能会同时更新共享参数。这种并行更新可能会导致线程间的冲突，比如在线程1加载全局参数w1之后，线程2还没等线程1存储全局参数更新后的值，就也对全局参数w1进行加载，这样导致每个线程都会存储值对W1计算的的更新后的全局参数值，直观的感觉是这应该会对学习的过程产生负面影响。但当对模型访问的稀疏性（sparity）做一定的限定后，这种访问冲突实际上是非常有限的。这正是Hogwild！算法收敛性存在的理论依据。异步SGD和Hogwild!算法

在计算策略的优势时，采用前向视角（forward view）的n步回报，而不是后向视角（backward view）。的别在于如何计算多步的奖励。

路径衍生策略梯度（pathwise derivative policy gradient）

另一种策略梯度的方法pathwise derivative策略梯度，应用到确定性策略的环境，用Qlearning求解连续动作的方法。

例子：SVG：将pathwise derivative（PD）应用到MDP中

漫谈重参数：从正态分布到Gumbel Softmax

Advanced Policy Gradient - pathwise derivative

四、DDPG

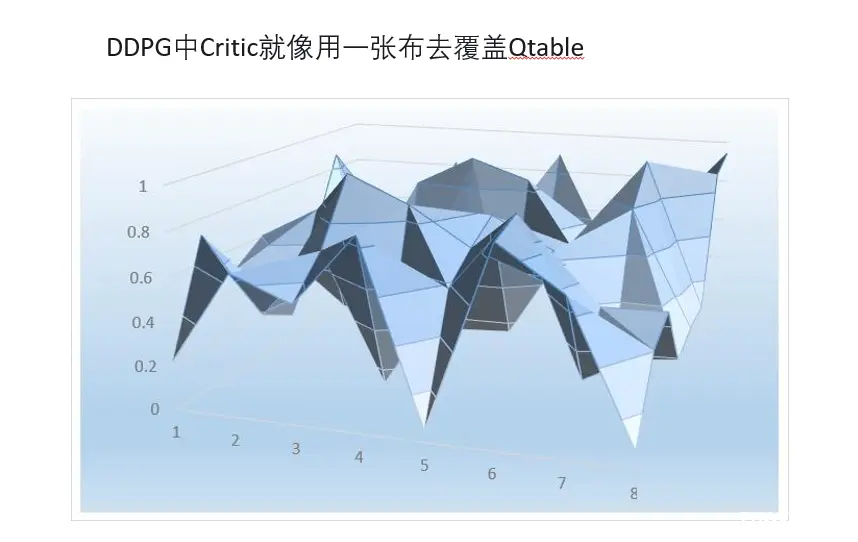
形象地理解DDPG。

DDPG中Critic（拟合Q值的网络）就像用一张布去覆盖的Qtable。当把某个state输入到DDPG的Actor中的时候，相当于在这块布上做沿着state所在的位置剪开，边缘是一条曲线。曲线是在某个状态下，选择某个动作值的时候，能获得的Q值。Actor的任务就是在寻找这个曲线的最高点，然后返回能获得这个最高点，也是最大Q值的动作。

DDPG深度确定性策略梯度（deep deterministic policy gradient，DDPG）构造一个确定性策略，用梯度上升的方法来最大化

Q

Q

Q值。DDPG 也属于一种 Actor-Critic 算法。之前学习的 REINFORCE、 PPO 学习随机性策略，而 DDPG 学习一个确定性策略。更新策略用的不是V，是Q

DQN不能用于连续控制问题原因，DQN用神经网络解决了Qlearning不能解决的连续状态空间问题。那同样的DDPG就是用策略网络Actor解决DQN不能解决的连续动作问题。用一策略网络直接替代maxQ(s’,a’)的功能。输入状态s，策略网络Actor返回动作action的取值（力矩），这个取值能够让q值最大，通过梯度上升更新策略网络。Critic网络的作用是预估Q，不是V；

在实做的时候，需要4个网络。actor, critic, Actor_target, cirtic_target。

Deep Deterministic Policy Gradient (DDPG)

DDPG流程：

五、Twin Delayed DDPG（TD3）双延迟深度确定性策略梯度

TD3：DDPG的改进，改进了三个方面

（一）double network

高估问题，本质还是DQN，DQN中采用max操作由于神经网络的误差啊会产生过估计问题，在DDPG中使用了一个Actor策略网络代替max操作，使用梯度上升来寻找最大值，是起到了argmax的作用的，所以说这里都进行了最大值选取的操作（无论是DQN的argmax还是DDPG的梯度上升），所以还是存在高估高估。DQN中计算targetQ值使用了doubleDqn的操作来减少max的影响，TD3使用多个Critic估计Q值取小值计算targetQ，实验得到两个就够用。

在目标网络中，这两个critic估算出来的Q值会用min()函数求出较少值作为更新的目标，更新两个网络 Critic网络_1 和 Critic网络_2。这两个网络完全独立，只是都用同一个目标进行更新。（虽然更新目标一样，两个网络会越来越趋近与和实际q值相同。但由于网络参数的初始值不一样，会导致计算出来的值有所不同。所以我们可以有空间选择较小的值去估算q值，避免q值被高估。）

（二）延迟的策略更新（delayed policy updates）

延迟的策略更新：学习过程中，Q值不断变化，覆盖Qtable的布不断变形。所以Actor要寻着最高点的任务困难。比如，本来是最高点的，当actor好不容易梯度上升去到最高点；Q值更新了，不是最高点了，actor只能转头再继续寻找新的最高点，还有可能陷入局部最优。

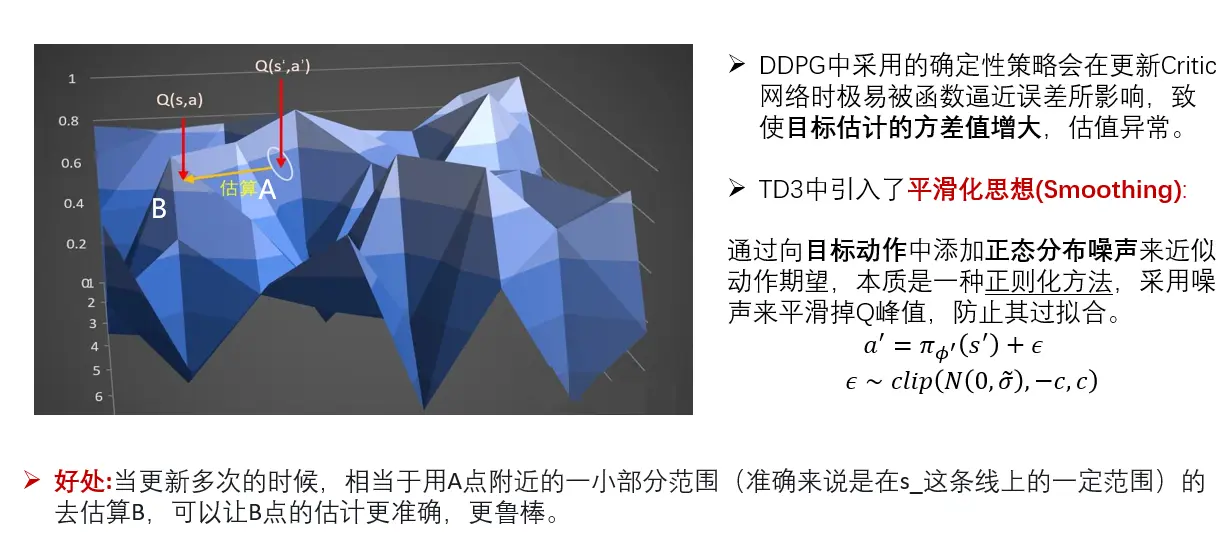
（三）目标策略平滑（target policy smoothing)

目标策略平滑，TD3不仅和DDPG一样，在探索的时候使用了探索噪声，而且还使用了策略噪声,TD3中,价值函数的更新目标每次都在action上加一个小扰动，计算targetQ时候，给targetQ网络输入s_和actor输出的a_后，给a加上噪音，让a在一定范围内随机。Q值函数的峰值往往会随着训练的进行而出现过拟合的情况，引入随机性来平滑掉Q值函数的峰值，防止其过拟合，从而提高算法的性能和稳定性。

计算target的时候，actor加上noise，是为了预估更准确，网络更有健壮性。

更新actor的时候不需要加上noise，希望actor能够寻着最大值,加上noise没有任何意义。

TD3

Advanced Policy Gradient - pathwise derivative