一、PyTorch是什么

PyTorch 由Facebook开源的神经网络框架，专门针对 GPU 加速的深度神经网络（DNN）编程。

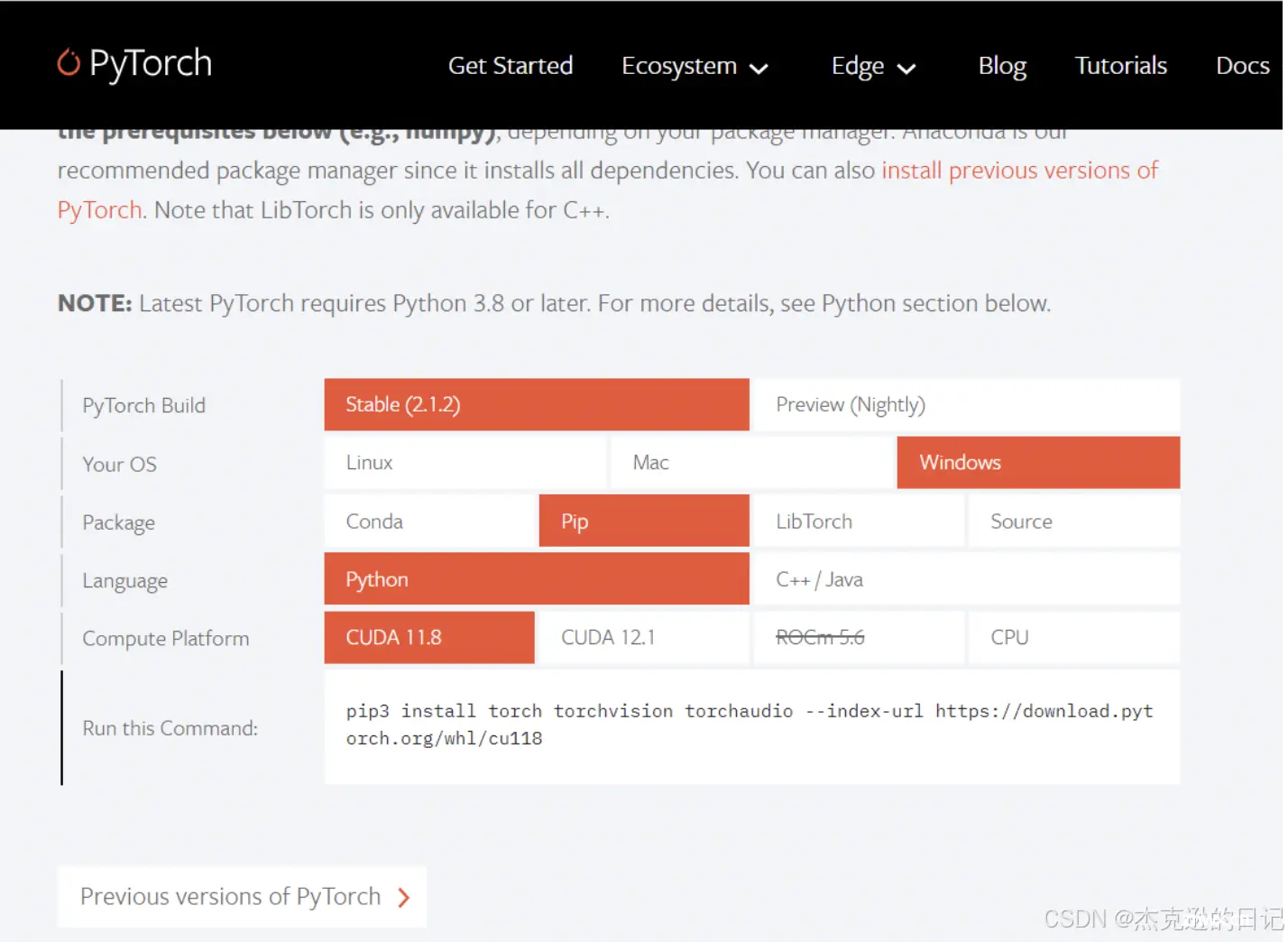
二、PyTorch安装

首先确保你已经安装了GPU环境，即Anaconda、CUDA和CUDNN

随后进入Pytorch官网​​​​​​PyTorch

官网会自动显示符合你电脑配置的Pytorch版本，复制指令到cuda环境中运行即可

测试是否安装成功

三、Tensor数据结构

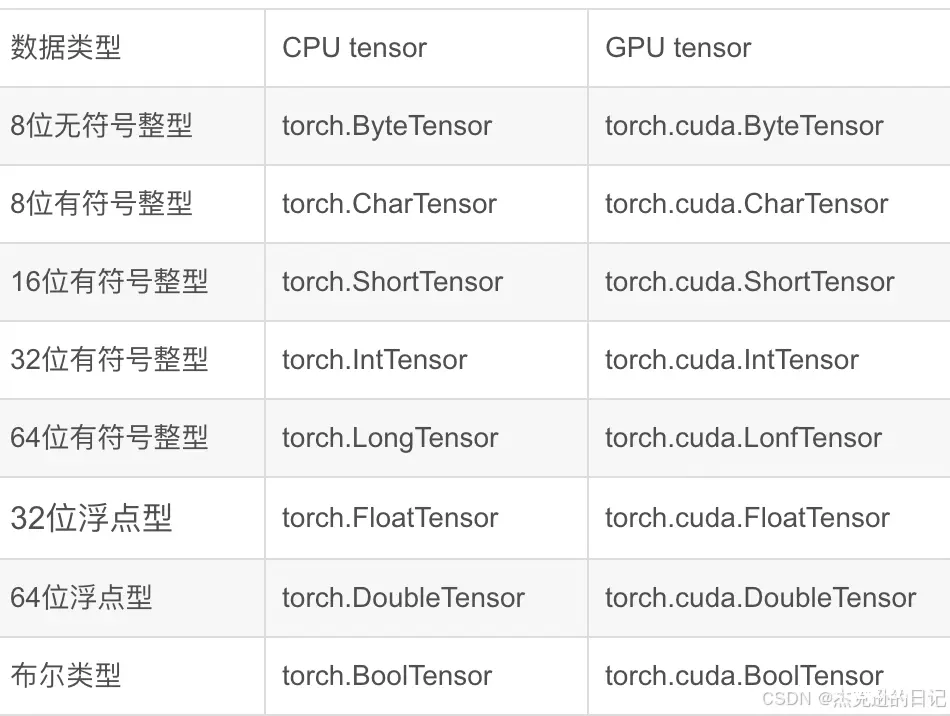
Tensor张量是Pytorch里最基本的数据结构。直观上来讲，它是一个多维矩阵，支持GPU加速，其基本数据类型如下

3.1 Tensor创建

3.1.1 torch.tensor() && torch.tensor([])

二者的主要区别在于创建的对象的size和value不同

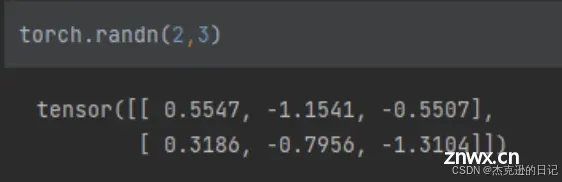
2.1.2 torch.randn && torch.randperm

生成的数据类型为浮点型，与numpy.randn生成随机数的方法类似，生成的浮点数的取值满足均值为0，方差为1的正态分布

torch.randpern(n)为创建一个n个整数，随机排列的Tensor

3.1.3 torch.range(begin，end，step)

生成一个一维的Tensor，三个参数分别的起始位置，终止位置和步长

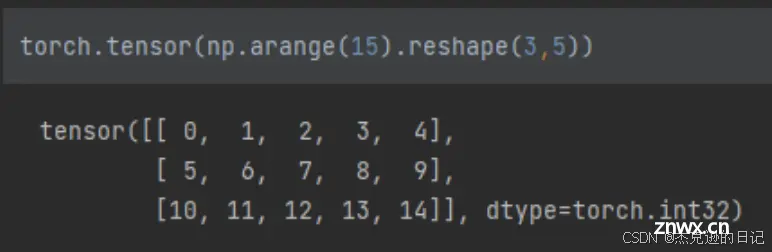
3.1.4 指定numpy

很多时候我们需要创建指定的Tensor，而numpy就是一个很好的方式

3.2 Tensor运算

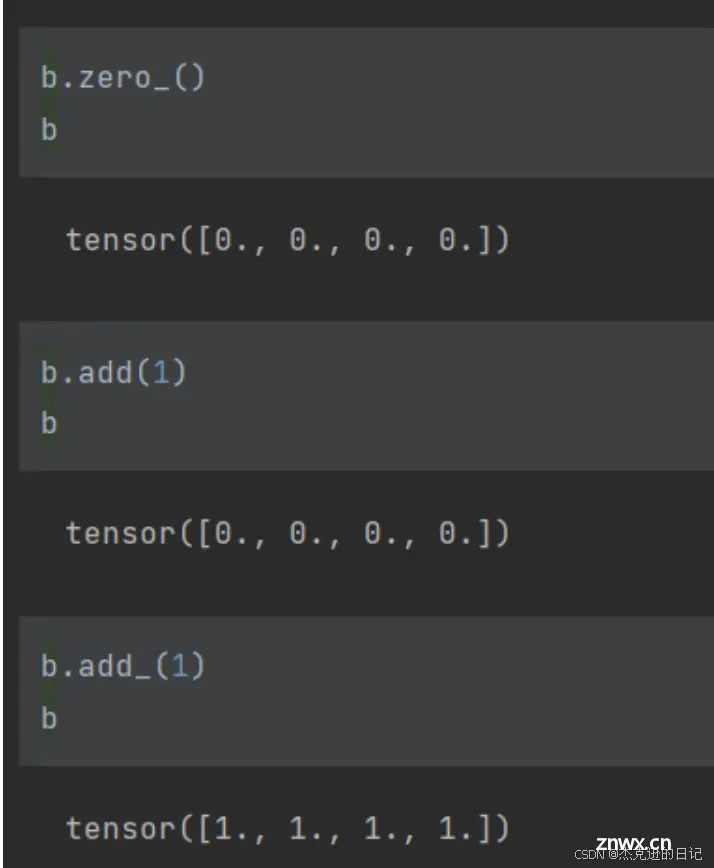
3.2.1 A.add() && A.add_()

所有的带_符号的函数都会对原数据进行修改

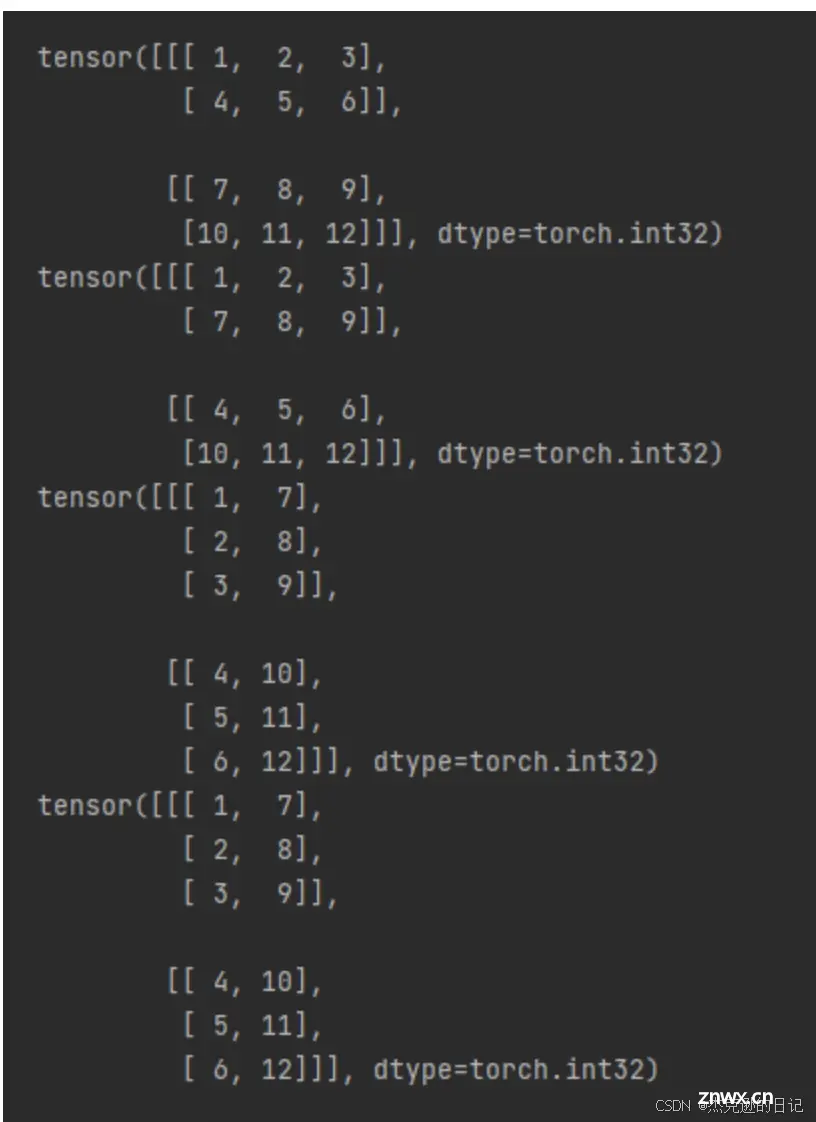
2.2.2 torch.stack

stack为拼接函数，函数的第一个参数为需要拼接的Tensor，第二个参数为细分到哪个维度

dim=0，C1 = [ A,B ]

dim=1，C2 = [ [ A[0],B[0] ] , [ A[1],B[1] ] ]

dim=2，C3 = [ [ [ A[0][0],B[0][0] ] , [ A[0][1],B[0][1] ] , [ A[0][2],B[0][2] ] ],

                        [ [ A[1][0],B[1][0] ] , [ A[1][1],B[1][1] ] , [ A[1][2],B[1][2] ] ] ]

dim=-1，C4 = C3

四、CUDA

CUDA是一种操作GPU的软件架构，Pytorch配合GPU环境这样模型的训练速度会非常的快

4.1 使用GPU

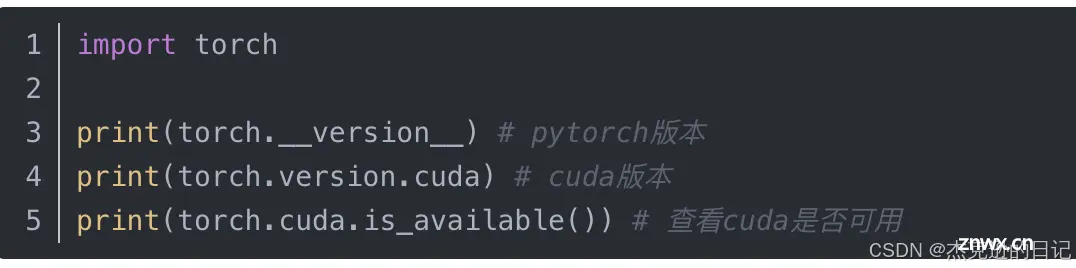
import torch

# 测试GPU环境是否可使用

print(torch.__version__) # pytorch版本

print(torch.version.cuda) # cuda版本

print(torch.cuda.is_available()) # 查看cuda是否可用

#使用GPU or CPU

device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

# 判断某个对象是在什么环境中运行的

a.device

# 将对象的环境设置为device环境

A = A.to(device)

# 将对象环境设置为COU

A.cpu().device

# 若一个没有环境的对象与另外一个有环境a对象进行交流,则环境全变成环境a

a+b.to(device)

# cuda环境下tensor不能直接转化为numpy类型,必须要先转化到cpu环境中

a.cpu().numpy()

# 创建CUDA型的tensor

torch.tensor([1,2],device)

五、其他技巧

5.1 自动微分

神经网络依赖反向传播求梯度来更新网络的参数，求梯度是个非常复杂的过程，在Pytorch中，提供了两种求梯度的方式，一个是backward，将求得的结果保存在自变量的grad属性中，另外一种方式是torch.autograd.grad

5.1.1 backward求导

使用backward进行求导。这里主要介绍了求导的两种对象，标量Tensor和非标量Tensor的求导。两者的主要区别是非标量Tensor求导的主要区别是加了一个gradient的Tensor，其尺寸与自变量X的尺寸一致。在求完导后，需要与gradient进行点积，所以只是一般的求导的话，设置的参数全部为1。最后还有一种使用标量的求导方式解决非标量求导，了解了解就好了。

import numpy as np

import torch

# 标量Tensor求导

# 求 f(x) = a*x**2 + b*x + c 的导数

x = torch.tensor(-2.0, requires_grad=True)

a = torch.tensor(1.0)

b = torch.tensor(2.0)

c = torch.tensor(3.0)

y = a*torch.pow(x,2)+b*x+c

y.backward() # backward求得的梯度会存储在自变量x的grad属性中

dy_dx =x.grad

dy_dx

# 非标量Tensor求导

# 求 f(x) = a*x**2 + b*x + c 的导数

x = torch.tensor([[-2.0,-1.0],[0.0,1.0]], requires_grad=True)

a = torch.tensor(1.0)

b = torch.tensor(2.0)

c = torch.tensor(3.0)

gradient=torch.tensor([[1.0,1.0],[1.0,1.0]])

y = a*torch.pow(x,2)+b*x+c

y.backward(gradient=gradient) 

dy_dx =x.grad

dy_dx

# 使用标量求导方式解决非标量求导

# 求 f(x) = a*x**2 + b*x + c 的导数

x = torch.tensor([[-2.0,-1.0],[0.0,1.0]], requires_grad=True)

a = torch.tensor(1.0)

b = torch.tensor(2.0)

c = torch.tensor(3.0)

gradient=torch.tensor([[1.0,1.0],[1.0,1.0]])

y = a*torch.pow(x,2)+b*x+c

z=torch.sum(y*gradient)

z.backward()

dy_dx=x.grad

dy_dx

5.1.2 autograd.grad求导

import torch

#单个自变量求导

# 求 f(x) = a*x**4 + b*x + c 的导数

x = torch.tensor(1.0, requires_grad=True)

a = torch.tensor(1.0)

b = torch.tensor(2.0)

c = torch.tensor(3.0)

y = a * torch.pow(x, 4) + b * x + c

#create_graph设置为True,允许创建更高阶级的导数

#求一阶导

dy_dx = torch.autograd.grad(y, x, create_graph=True)[0]

#求二阶导

dy2_dx2 = torch.autograd.grad(dy_dx, x, create_graph=True)[0]

#求三阶导

dy3_dx3 = torch.autograd.grad(dy2_dx2, x)[0]

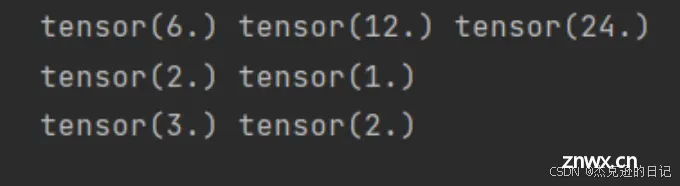
print(dy_dx.data, dy2_dx2.data, dy3_dx3)

# 多个自变量求偏导

x1 = torch.tensor(1.0, requires_grad=True)

x2 = torch.tensor(2.0, requires_grad=True)

y1 = x1 * x2

y2 = x1 + x2

#只有一个因变量,正常求偏导

dy1_dx1, dy1_dx2 = torch.autograd.grad(outputs=y1, inputs=[x1, x2], retain_graph=True)

print(dy1_dx1, dy1_dx2)

# 若有多个因变量，则对于每个因变量,会将求偏导的结果加起来

dy1_dx, dy2_dx = torch.autograd.grad(outputs=[y1, y2], inputs=[x1, x2])

dy1_dx, dy2_dx

print(dy1_dx, dy2_dx)

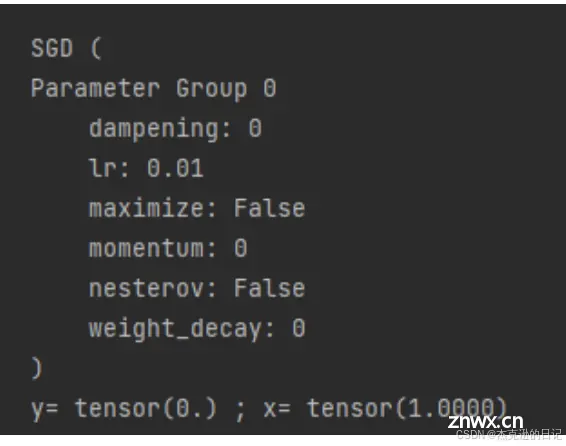
51.3 求最小值

使用自动微分机制配套使用SGD随机梯度下降来求最小值

#例2-1-3 利用自动微分和优化器求最小值

import numpy as np

import torch

# f(x) = a*x**2 + b*x + c的最小值

x = torch.tensor(0.0, requires_grad=True)  # x需要被求导

a = torch.tensor(1.0)

b = torch.tensor(-2.0)

c = torch.tensor(1.0)

optimizer = torch.optim.SGD(params=[x], lr=0.01)  #SGD为随机梯度下降

print(optimizer)

def f(x):

    result = a * torch.pow(x, 2) + b * x + c

    return (result)

for i in range(500):

    optimizer.zero_grad()  #将模型的参数初始化为0

    y = f(x)

    y.backward()  #反向传播计算梯度

    optimizer.step()  #更新所有的参数

print("y=", y.data, ";", "x=", x.data)

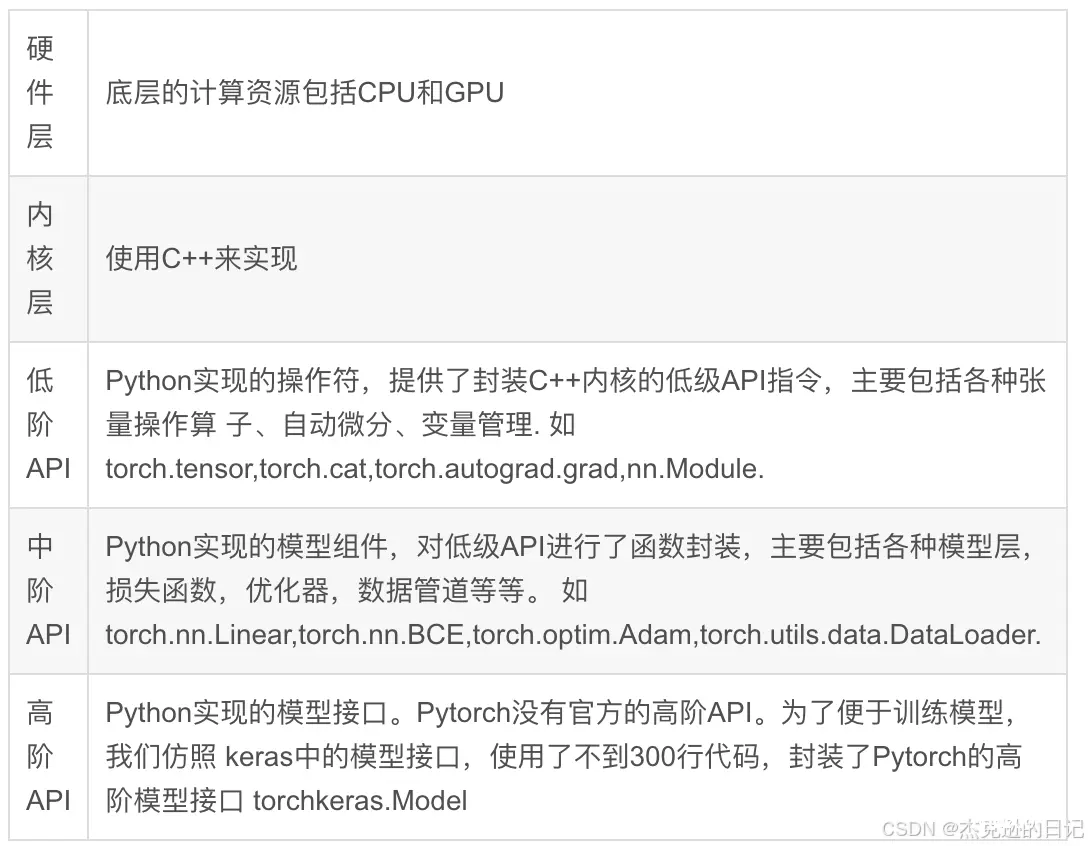
5.2 Pytorch层次结构

Pytorch中一共有5个不同的层次结构，分别为硬件层、内核层、低阶API、中阶API和高阶API（torchkeras）

六、数据

Pytorch主要通过Dataset和DataLoader进行构建数据管道

6.1 Dataset and DataLoader

6.2 数据读取与预处理

DataLoader的参数如下

DataLoader(

 dataset,

 batch_size=1,

 shuffle=False,

 sampler=None,

 batch_sampler=None,

 num_workers=0,

 collate_fn=None,

 pin_memory=False,

 drop_last=False,

 timeout=0,

 worker_init_fn=None,

 multiprocessing_context=None,

)

在实践中，主要修改的参数以下标为橙色

Epoch、Iteration、Batchsize之间的关系

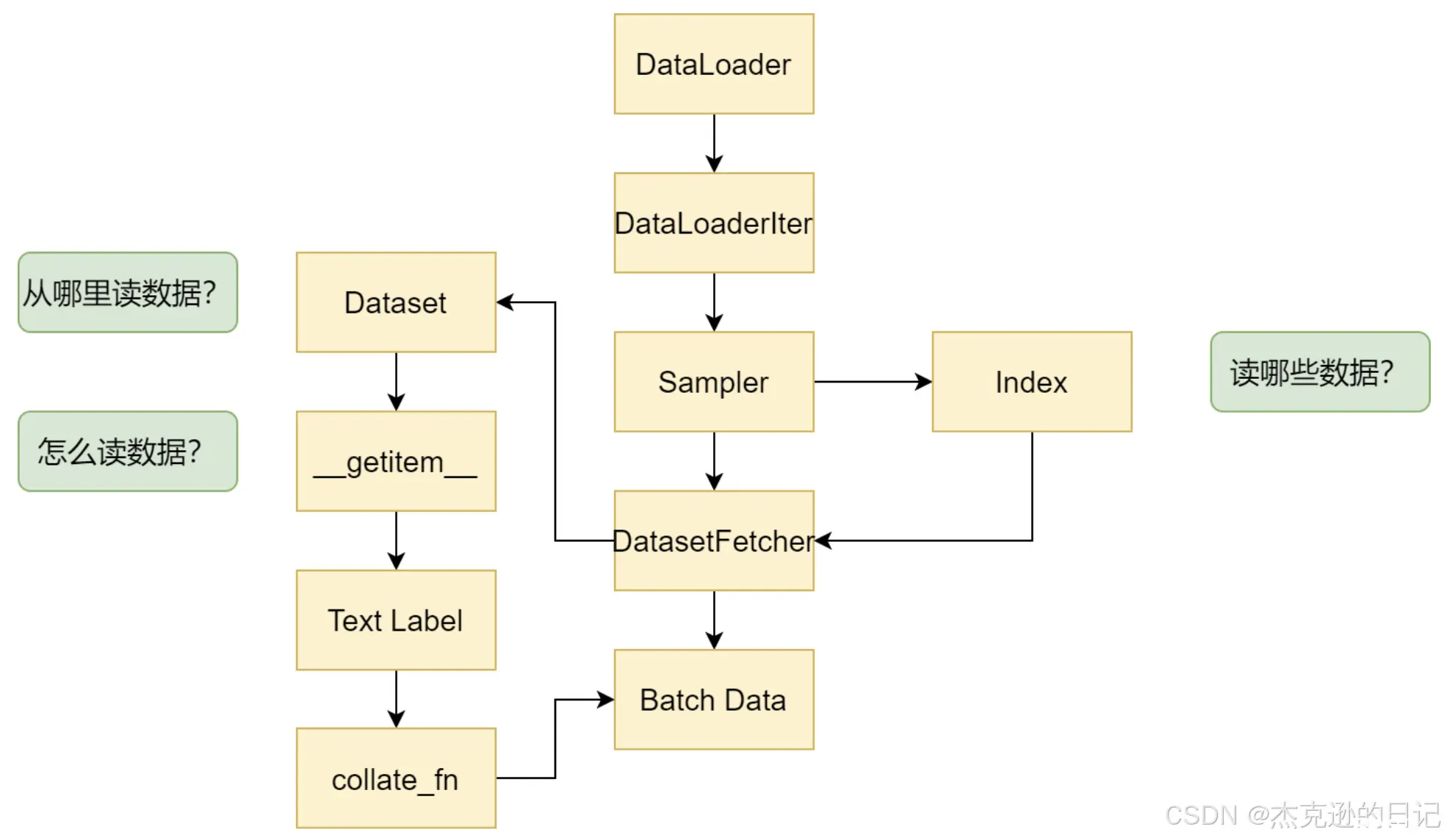
数据读取的主要流程

1. 从DataLoader开始

2. 进入DataLoaderIter，判断单线程还是多线程

3. 进入Sampler进行采样，获得一批一批的索引，这些索引告诉我们需要读取哪些数据、

4. 进入DatasetFetcher，依据索引读取数据

5. Dataset告诉我们数据的地址

6. 自定义的Dataset中会重写__getietm__方法，针对不同的数据来进行定制化的数据读取

7. 到这里就获取的数据的Text和Label

8. 进入collate_fn将之前获取的个体数据进行组合成batch

9. 一个一个batch组成Batch Data

具体的代码

from torch.utils.data import DataLoader

from torch.utils.data.dataset import TensorDataset

# 自构建数据集

dataset = TensorDataset(torch.arange(1, 40))

dl = DataLoader(dataset,

                batch_size=10,

                shuffle=True,

                num_workers=1,

                drop_last=True)

# 数据输出

for batch in dl:

    print(batch)

因为自定义的数据集只有39条，最后一个batch的数据量小于10，被舍弃掉了

而数据预处理主要是重写Dataset和DataLoader中的方法，因此总体代码如下所示

6.5 Pytorch工具

基于Pytorch已经产生了一些封装完备的工具，而缺点也很明显，数据处理不是很灵活，对于初学者来说，多写代码比较踏实，因此作者不太推荐使用这些方法

七、torch.nn

torch.nn是神经网路工具箱，该工具箱建立于Autograd(主要有自动求导和梯度反向传播功能)，提供了网络搭建的模组，优化器等一系列功能。

搭建一个神经网络模型整个流程是怎么样的呢？

搭建网络流程

1 数据读取

2 定义模型

3 定义损失函数和优化器

4 模型训练

5 获取训练结果

最简单的FNN网络来对经典数据集diabetes糖尿病数据集来进行分类预测，模型性能指标直接采用Loss。

数据集

​

import numpy as np

import torch

import matplotlib.pyplot as plt

from torch.utils.data import Dataset, DataLoader

# Prepare the dataset

class DiabetesDateset(Dataset):

    # 加载数据集

    def __init__(self, filepath):

        xy = np.loadtxt(filepath, delimiter=',', dtype=np.float32, encoding='utf-8')

        self.len = xy.shape[0]  # shape[0]是矩阵的行数,shape[1]是矩阵的列数

        self.x_data = torch.from_numpy(xy[:, :-1])

        self.y_data = torch.from_numpy(xy[:, [-1]])

    # 获取数据索引

    def __getitem__(self, index):

        return self.x_data[index], self.y_data[index]

    # 获得数据总量

    def __len__(self):

        return self.len

dataset = DiabetesDateset('diabetes.csv')

train_loader = DataLoader(dataset=dataset, batch_size=32, shuffle=True, num_workers=2, drop_last=True)  # num_workers为多线程

# Define the model

class FNNModel(torch.nn.Module):

    def __init__(self):

        super(FNNModel, self).__init__()

        self.linear1 = torch.nn.Linear(8, 6)  # 输入数据的特征有8个,也就是有8个维度,随后将其降维到6维

        self.linear2 = torch.nn.Linear(6, 4)  # 6维降到4维

        self.linear3 = torch.nn.Linear(4, 2)  # 4维降到2维

        self.linear4 = torch.nn.Linear(2, 1)  # 2w维降到1维

        self.sigmoid = torch.nn.Sigmoid()  # 可以视其为网络的一层,而不是简单的函数使用

    def forward(self, x):

        x = self.sigmoid(self.linear1(x))

        x = self.sigmoid(self.linear2(x))

        x = self.sigmoid(self.linear3(x))

        x = self.sigmoid(self.linear4(x))

        return x

model = FNNModel()

# Define the criterion and optimizer

criterion = torch.nn.BCELoss(reduction='mean')  # 返回损失的平均值

optimizer = torch.optim.SGD(model.parameters(), lr=0.01)

epoch_list = []

loss_list = []

# Training

if __name__ == '__main__':

    for epoch in range(100):

        # i是一个epoch中第几次迭代,一共756条数据,每个mini_batch为32,所以一个epoch需要迭代23次

        # data获取的数据为(x,y)

        loss_one_epoch = 0

        for i, data in enumerate(train_loader, 0):

            inputs, labels = data

            y_pred = model(inputs)

            loss = criterion(y_pred, labels)

            loss_one_epoch += loss.item()

            optimizer.zero_grad()

            loss.backward()

            optimizer.step()

        loss_list.append(loss_one_epoch / 23)

        epoch_list.append(epoch)

        print('Epoch[{}/{}],loss:{:.6f}'.format(epoch + 1, 100, loss_one_epoch / 23))

    # Drawing

    plt.plot(epoch_list, loss_list)

    plt.xlabel('epoch')

    plt.ylabel('loss')

    plt.show()

​运行结果