【人工智能】--强化学习(2.0)
Papicatch 2024-07-20 12:31:01 阅读 54


个人主页:欢迎来到 Papicatch的博客
课设专栏 :学生成绩管理系统
专业知识专栏: 专业知识
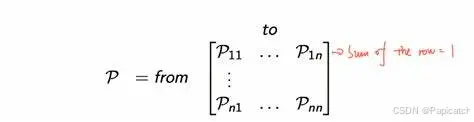
文章目录
🍉强化学习与有监督学习的区别
🍈数据特点
🍈学习目标
🍈反馈机制
🍈策略优化
🍈应用场景
🍉强化学习的特点
🍈试错学习
🍈延迟奖励
🍈策略优化
🍈环境交互
🍈 不确定性
🍈自主性
🍈应用广泛
🍉强化学习组成部分
🍈智能体
🍍感知能力
🍍决策能力
🍍行动能力
🍈奖励
🍈状态
🍍多样性
🍍影响决策
🍍动态性
🍈环境
🍍环境的定义和组成
🍍环境的特性
🍉马尔科夫决策过程(Markov Decision Process,MDP)
🍈定义
🍈核心概念
🍈价值函数
🍈奖励过程
🍍代码实现
🍉动态规划
🍈基本思想
🍈关键概念
🍈工作原理
🍈优缺点
🍍优点
🍍缺点
🍉强化学习基于值函数的学习方法
🍈值函数的定义
🍈常见的基于值函数的学习方法
🍍蒙特卡罗方法(Monte Carlo Method)
🍍时序差分学习(Temporal Difference Learning)
🍍SARSA 算法
🍈值函数的更新规则
🍍优点
🍍缺点
🍉基于策略函数的学习方法
🍈策略函数的定义
🍈常见的基于策略函数的学习方法
🍍策略梯度算法(Policy Gradient Algorithm)
🍍Actor-Critic 算法
🍈策略梯度的计算
🍍优点
🍍缺点
🍉Actor-Critic 算法
🍈基本原理
🍈工作流程
🍈优势
🍈常见变体
🍈示例
🍍示例分析
🍍代码实现
🍉总结

本篇文章可以配合:人工智能强化学习:核心内容、社会影响及未来展望 食用喔!!!

🍉强化学习与有监督学习的区别
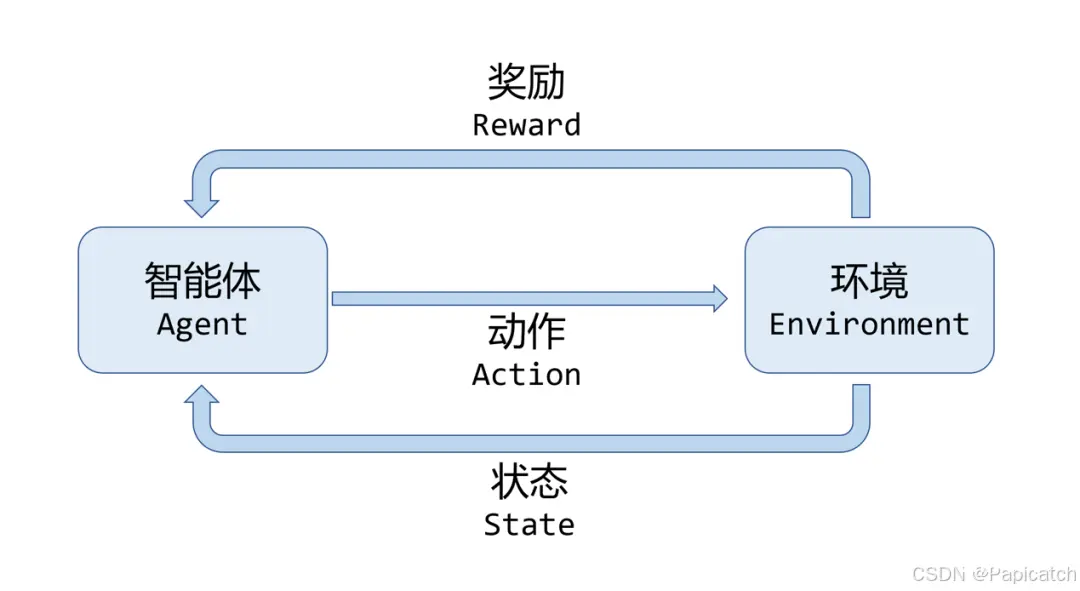
强化学习解决问题流程
强化学习和有监督学习是机器学习中的两个重要分支,它们在许多方面存在显著的区别。
🍈数据特点
在有监督学习中,数据通常以一组输入特征和对应的正确输出标签的形式呈现。例如,在图像分类任务中,输入是图像的像素值,输出是图像所属的类别标签。而强化学习的数据是智能体与环境交互产生的一系列状态、动作和奖励。
🍈学习目标
有监督学习的目标是学习一个能够准确预测给定输入的输出的模型。比如,通过学习大量已标注的猫狗图片,模型能够准确判断新输入的图片是猫还是狗。强化学习的目标则是让智能体通过与环境的交互,学习到能够获得最大累积奖励的策略,以实现长期的最优决策。
🍈反馈机制
有监督学习中,模型在每次预测后会立即得到明确的正确与否的反馈。比如预测结果与真实标签进行对比,计算损失并进行优化。但在强化学习中,智能体的动作所产生的奖励通常是延迟和稀疏的。也就是说,智能体可能需要执行一系列动作后,才能得到一个奖励信号,而且奖励并非在每个动作后都能及时获得。
🍈策略优化
有监督学习主要是优化模型的参数以最小化预测误差。强化学习则是通过不断尝试不同的动作,根据奖励来调整策略,以找到最优的行动策略。
🍈应用场景
有监督学习常用于图像识别、语音识别、文本分类等任务。例如,识别手写数字、语音转文字等。强化学习则更适用于需要做出连续决策的场景,如机器人控制、游戏策略制定、自动驾驶等。
举个例子来说,在训练一个下棋的模型时,如果使用有监督学习,可能是让模型学习大量人类高手的棋局,预测下一步的走法。而如果使用强化学习,模型会通过自己与自己对弈,根据胜负结果来不断调整策略,学习如何下棋才能赢得更多。
🍉强化学习的特点

强化学习具有以下几个显著的特点
🍈试错学习
智能体通过不断地尝试不同的动作来与环境进行交互,从成功和失败的经验中学习。它没有先验的正确答案,只能通过不断的试验来逐渐优化自己的策略。例如,一个机器人学习如何在复杂的地形中行走,可能会经历多次摔倒和错误的步伐,最终找到稳定的行走方式。
🍈延迟奖励
强化学习中的奖励通常不是即时给出的,而是在一系列动作之后才会显现。这意味着智能体需要考虑长期的回报,而不仅仅是眼前的利益。比如,在股票投资中,一系列的买卖决策可能要经过一段时间才能确定是否获得了良好的收益。
🍈策略优化
强化学习的核心目标是找到最优的策略,即给定一个状态,智能体应该采取什么样的动作来最大化未来的累积奖励。这个策略会随着学习的进行不断调整和优化。
🍈环境交互
智能体与动态的环境进行持续的交互,环境的状态会因为智能体的动作而发生改变。例如,在自动驾驶中,车辆的行驶动作会改变周围的交通状况。
🍈 不确定性
由于环境的复杂性和随机性,强化学习的结果往往具有一定的不确定性。即使在相同的初始条件下,多次学习的结果也可能会有所不同。
🍈自主性
智能体具有自主学习和决策的能力,不需要人类明确地告诉它每一步应该怎么做,而是通过自身与环境的交互来探索和发现最优策略。
🍈应用广泛
可以应用于众多领域,如机器人控制、游戏、资源管理、金融交易等,能够解决各种需要动态决策的问题。
以训练一个智能机器人打扫房间为例,它可能一开始会随意移动和操作,导致效率低下甚至造成混乱。但通过不断的试错和接收延迟的奖励(房间变得整洁干净),它逐渐优化自己的动作策略,学会更高效地完成打扫任务。
🍉强化学习组成部分

🍈智能体
在强化学习的领域中,智能体(Agent)是一个至关重要的概念。
智能体可以被理解为具有感知、决策和行动能力的实体。它能够与环境进行交互,并根据环境的反馈来调整自己的行为策略,以实现特定的目标。
🍍感知能力
智能体能够感知环境的状态。这可能包括获取各种信息,如位置、速度、周围物体的状态等。例如,在自动驾驶场景中,智能体可以通过传感器感知车辆的速度、与其他车辆的距离和道路状况。
🍍决策能力
基于所感知到的环境状态,智能体能够做出决策,决定采取何种行动。决策过程通常基于其内部的学习模型和策略。例如,在围棋游戏中,智能体根据棋盘的局面决定下一步落子的位置。
🍍行动能力
智能体能够将决策转化为实际的行动,并对环境产生影响。例如,机器人智能体可以执行移动、抓取物体等物理动作。智能体的行为并非一成不变,而是通过不断的学习和优化来改进。在强化学习中,智能体通过与环境的反复交互,接收奖励或惩罚的反馈,从而逐渐调整其策略,以追求更多的奖励和更好的性能。以一个自动化交易的智能体为例,它会感知市场的各种数据(如股票价格、成交量等),基于这些信息做出买入或卖出的决策,然后执行交易操作。随着时间的推移,它会根据交易的结果(盈利或亏损)来调整自己的交易策略,以期望在未来获得更高的收益。再比如,一个在迷宫中探索的智能体,它会感知自己在迷宫中的位置和周围的通道情况,决定前进的方向,然后移动。如果它找到了出口,会得到正奖励,否则可能得到负奖励。通过多次尝试,智能体逐渐学会如何更快地找到出口。
总之,智能体是强化学习中的核心元素,其感知、决策和行动的能力,以及不断学习和优化的特性,使得它能够在复杂的环境中不断适应和改进,以实现各种任务和目标。
🍈奖励
在强化学习中,奖励(Reward)是一个标量反馈信号,用于衡量智能体在某个时刻所采取的动作的表现。其核心作用是引导智能体学习最优策略,以最大化累计奖励值。
具体来说,强化学习基于奖励假设(Reward Hypothesis),即所有的目标都可以被描述为最大化期望的累计奖励值。这意味着智能体的目标是通过选择合适的动作序列,来尽可能多地获得奖励。
不同的强化学习任务对应着不同的奖励设置。例如:
在直升机特技表演任务中,当直升机按照期望轨迹飞行时会给出正奖励,若坠机则给出负奖励;围棋游戏里,下赢一局给出正奖励,输了则给出负奖励;投资组合问题中,每获得定量收益时给出正奖励;发电站控制时,每获得新的能源给出正奖励,超过安全阈值则给出负奖励;控制人形机器人行走时,每次向前移动给一个正奖励,每次摔倒给一个负奖励;玩不同的电子游戏时,当分数增加和减少时,分别给出正负奖励。
奖励可以是即时的,也可能具有延迟性。智能体的动作可能会在很长时间后才产生显著的奖励,这就需要智能体考虑长期的回报,而不仅仅是眼前的利益。例如,一个金融投资策略可能需要数月才能获得收益,即当前的动作可能有非常久远的影响;给直升机加油这个动作可能会使直升机在未来几个小时免于坠毁。
在每个时刻 t,智能体接收上一个动作的奖励值与当前时刻的观测,之后执行动作;环境则接受智能体的动作,并反馈出当前动作的奖励值以及下一个时刻的观测值,整个过程随着时间 t 的推进而不断延伸。
奖励的设置对于强化学习算法的性能和收敛速度有着至关重要的影响。如果奖励设置不合理,可能导致智能体学习到不理想的策略,或者难以收敛到最优策略。例如,如果奖励过于稀疏,智能体可能很难确定哪些动作是有益的;而如果奖励设置不当,智能体可能会学会一些“投机取巧”的方式来获取奖励,而不是真正实现任务的目标。
在实际应用中,设计合适的奖励函数是一项具有挑战性的任务,需要对具体问题有深入的理解,并且可能需要不断地尝试和调整。有时候,为了鼓励智能体进行探索或避免其陷入局部最优,还会采用一些奖励塑造(Reward Shaping)的方法。例如基于势能的奖励塑造(Potential-based Reward Shaping),通过给每个状态设定势能,从势能低的地方到势能高的地方给予正奖励,从势能高的地方回势能低的地方给予负奖励,从而引导智能体的行为,同时保证最优策略的不变性。
🍈状态
在强化学习中,状态(state)是对环境或系统当前情况的描述。它是智能体进行决策和学习的依据。
状态可以包含各种信息,具体取决于所解决的问题和应用场景。例如,在自动驾驶中,状态可能包括车辆的速度、位置、周围车辆和障碍物的状态等;在棋类游戏中,状态可以表示棋盘上各个棋子的位置;在机器人控制中,状态可能涉及机器人的关节角度、传感器读数等。
状态具有以下几个重要特点:
🍍多样性
不同的任务和环境中,状态的形式和内容可以有很大差异。
🍍影响决策
智能体根据当前的状态来选择采取何种动作。
🍍动态性
随着时间的推移和智能体与环境的交互,状态会发生变化。
从数学角度来看,状态是强化学习中马尔可夫决策过程(MDP)的一个关键元素。下一个状态的概率通常仅依赖于当前状态和当前采取的动作,这被称为马尔可夫性。
状态在强化学习中的作用主要体现在以下方面:
提供信息:帮助智能体了解环境的情况,以便做出合适的决策。确定策略:不同的状态可能对应着不同的最优动作,通过学习,智能体可以根据状态来确定采取什么样的动作以获得最大的累积奖励。更新和优化:智能体根据从环境中获得的奖励以及新的状态,来更新其对状态价值的估计,进而优化策略。
例如,在一个简单的迷宫游戏中,状态可以是智能体在迷宫中的位置。智能体根据当前所处的位置(状态),决定是向左、向右、向前还是向后移动(动作)。移动后会到达新的位置(新的状态),并可能获得一定的奖励(例如找到宝藏获得正奖励,撞到墙壁获得负奖励)。智能体通过不断尝试不同的动作,根据获得的奖励和经历的状态序列,学习到在不同位置(状态)下应该采取何种动作(策略),以最大化累积奖励。
🍈环境
在强化学习中,环境(Environment)是一个至关重要的概念,它与智能体相互作用,对智能体的学习和决策产生深远影响。
🍍环境的定义和组成
环境是智能体之外的一切事物,包括物理世界、其他实体、规则和条件等。它由多个部分组成,例如状态空间(State Space),即所有可能的环境状态的集合;动作空间(Action Space),表示智能体可以采取的所有可能动作;以及奖励函数(Reward Function),用于根据智能体的动作和环境状态给出相应的奖励。
🍍环境的特性
动态性:环境的状态会随着时间和智能体的动作而不断变化。例如,在机器人足球比赛中,球的位置、队友和对手的位置都在实时改变。不确定性:环境中可能存在随机因素,使得相同的动作在不同情况下产生不同的结果。比如,在股票市场中,即使采取相同的投资策略,由于市场的不确定性,收益也可能不同。复杂性:环境可能非常复杂,包含大量的变量和相互关系。例如,在城市交通系统中,需要考虑车辆、行人、信号灯等众多因素。
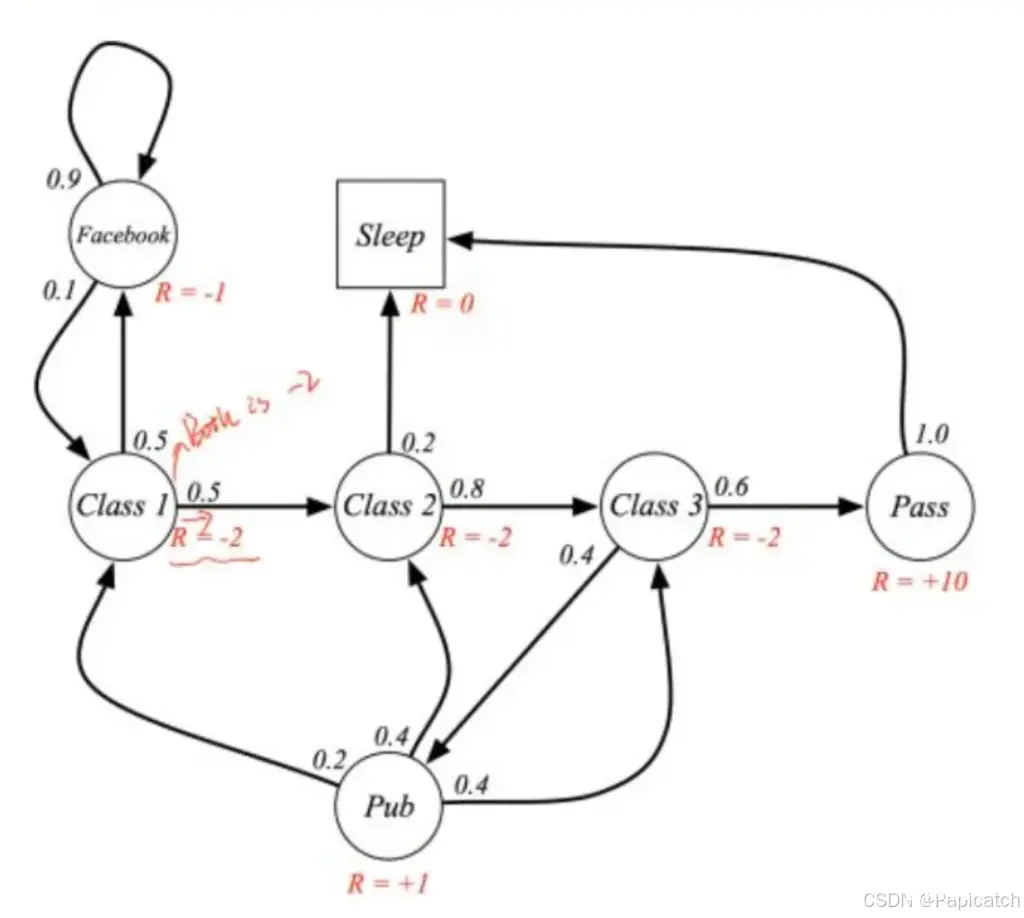
🍉马尔科夫决策过程(Markov Decision Process,MDP)
🍈定义

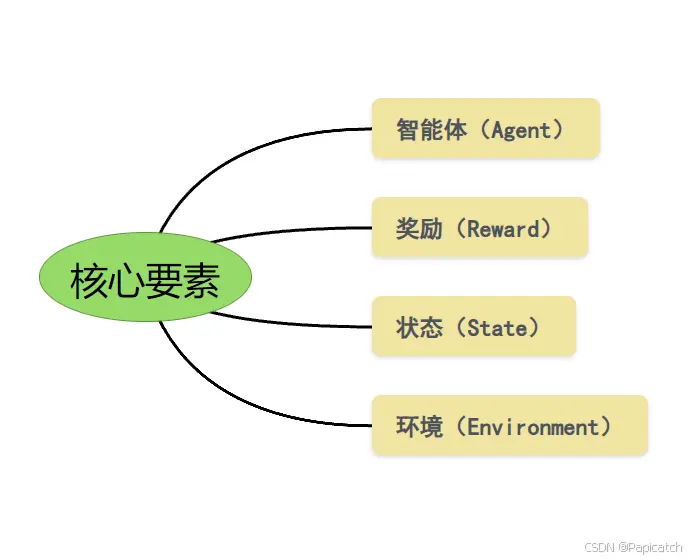
马尔科夫决策过程是一个五元组(S、A、P、R、γ),其中:
是状态的有限集合。 是动作的有限集合。 是状态转移概率矩阵,
表示在状态 s 采取动作 a 转移到状态 s' 的概率。 是奖励函数,
表示在状态 s 采取动作 a 所获得的即时奖励。 是折扣因子,用于权衡未来奖励的重要性,取值在 [0,1] 之间。
🍈核心概念
马尔科夫性:未来的状态只取决于当前状态和当前采取的动作,而与过去的历史无关。策略:是从状态到动作的映射,即给定一个状态,决定采取何种动作。
🍈价值函数

包括状态价值函数 V(s) 和动作价值函数 Q(s,a) 。
状态价值函数表示从状态 s 开始,遵循当前策略所获得的期望累积折扣奖励。动作价值函数表示在状态 s 采取动作 a ,遵循当前策略所获得的期望累积折扣奖励。
🍈奖励过程

马尔可夫奖励过程MRP
🍍代码实现
<code>import numpy as np
# 定义状态数量
num_states = 3
# 定义状态转移概率矩阵
transition_matrix = np.array([
[0.1, 0.6, 0.3],
[0.4, 0.3, 0.3],
[0.2, 0.5, 0.3]
])
# 定义奖励向量
rewards = np.array([1, 2, 3])
# 折扣因子
gamma = 0.9
# 计算价值函数
def compute_value_function():
value = np.zeros(num_states)
threshold = 1e-6
delta = float('inf')
while delta > threshold:
new_value = np.copy(value)
for state in range(num_states):
value_ = 0
for next_state in range(num_states):
value_ += transition_matrix[state, next_state] * (rewards[next_state] + gamma * value[next_state])
new_value[state] = value_
delta = np.max(np.abs(new_value - value))
value = new_value
return value
value_function = compute_value_function()
print("价值函数:", value_function)

🍉动态规划
在强化学习中,动态规划(Dynamic Programming)是一种用于解决最优控制问题的有效方法。
🍈基本思想
将复杂的问题分解为一系列更简单的子问题,并通过存储和复用子问题的解来提高计算效率。
🍈关键概念
策略评估(Policy Evaluation):给定一个策略,计算该策略下每个状态的价值函数。策略改进(Policy Improvement):基于当前的价值函数,找到一个更好的策略。策略迭代(Policy Iteration):通过交替进行策略评估和策略改进,逐步收敛到最优策略。价值迭代(Value Iteration):直接迭代价值函数,以找到最优价值函数,从而得到最优策略。
🍈工作原理
假设我们有一个有限的状态空间和动作空间,以及已知的环境模型(包括状态转移概率和奖励函数)。
在策略评估中,通过反复应用贝尔曼期望方程来更新状态价值,直到收敛。策略改进通过比较当前策略下每个状态的动作价值来确定是否有更好的动作选择。策略迭代不断重复评估和改进的过程,直到策略不再改变。价值迭代则更快地收敛到最优价值函数。
🍈优缺点
🍍优点
能保证在有限的状态和动作空间中找到最优解,如果环境模型准确。具有良好的理论基础和数学性质。
🍍缺点
对于大规模问题,由于需要存储大量的状态值和计算复杂的转移概率,计算量可能非常大。通常需要对环境有完整的了解,这在实际应用中往往难以满足。
例如,考虑一个简单的迷宫问题,状态是迷宫中的位置,动作是向四个方向移动。通过动态规划,可以计算出从每个位置出发采取最优策略能够获得的累积奖励,从而找到走出迷宫的最佳路径。
🍉强化学习基于值函数的学习方法
在强化学习中,基于值函数的学习方法是一类重要的策略学习途径。
🍈值函数的定义
值函数用于评估在特定状态下采取某种策略的长期期望回报。常见的值函数包括状态值函数(State Value Function,V(s))和动作值函数(Action Value Function,Q(s,a))。
🍈常见的基于值函数的学习方法
🍍蒙特卡罗方法(Monte Carlo Method)
通过多次采样完整的状态-动作序列来估计值函数。优点是直接估计期望回报,无需对环境的动态模型有先验了解。例如,在玩纸牌游戏中,多次重复游戏过程,根据最终的输赢结果来评估每个状态的价值。
🍍时序差分学习(Temporal Difference Learning)
结合了蒙特卡罗方法和动态规划的思想。基于当前的奖励和对下一状态值函数的估计来更新当前状态的值函数。例如,Q-learning 算法就是一种典型的时序差分算法。
🍍SARSA 算法
也是一种时序差分算法。与 Q-learning 的区别在于更新值函数时使用的动作不同。
🍈值函数的更新规则
以 Q-learning 为例,其更新规则为:

其中,a 是学习率,γ 是折扣因子,
是在状态

采取动作

获得的即时奖励,

是下一状态。
🍍优点
能够为策略的改进提供明确的方向。相对较为稳定和收敛。
🍍缺点
对于连续状态和动作空间,计算和存储值函数可能变得困难。可能会陷入局部最优。
例如,在一个机器人导航任务中,通过基于值函数的学习方法,机器人可以学习到在不同位置采取何种动作能够更快地到达目标位置,从而实现高效的导航。
🍉基于策略函数的学习方法
🍈策略函数的定义
策略函数
表示在状态 s 下采取动作 a 的概率分布。
🍈常见的基于策略函数的学习方法
🍍策略梯度算法(Policy Gradient Algorithm)
通过计算策略的梯度来更新策略参数,以最大化期望回报。例如,REINFORCE 算法就是一种简单的策略梯度算法。
🍍Actor-Critic 算法
结合了策略函数(Actor)和值函数(Critic)。Critic 用于评估当前策略的好坏,Actor 根据 Critic 的反馈来更新策略。
🍈策略梯度的计算
以 REINFORCE 算法为例,策略梯度的计算公式为:
其中,θ 是策略的参数,γ 是状态-动作轨迹,Gt 是从时间步 t 开始的累积回报。
🍍优点
能够处理连续的动作空间。直接对策略进行优化,避免了值函数估计的误差传播。
🍍缺点
方差较大,导致训练不稳定。通常需要更多的样本数据来获得较好的性能。
例如,在控制机械臂抓取物体的任务中,基于策略函数的学习方法可以让机械臂学习到如何以不同的姿态和力度抓取物体,以提高抓取的成功率。
🍉Actor-Critic 算法
Actor-Critic 算法是强化学习中一种结合了策略梯度(Actor)和价值估计(Critic)的方法。
🍈基本原理
Actor(策略网络):负责根据当前状态生成动作,其策略用 π(a|s;θ) 表示,其中 θ 是策略网络的参数。Critic(价值网络):用于评估 Actor 所采取动作的好坏,估计状态值函数 V(s;w) 或动作值函数 ,其中 S(s,a;w) 是价值网络的参数。
🍈工作流程
Actor 根据当前状态选择一个动作。环境接收动作,给出新的状态和奖励。Critic 根据状态和奖励估计价值。基于 Critic 的价值评估,Actor 调整策略参数以优化未来的动作选择。
🍈优势
结合了策略梯度方法直接优化策略和基于值函数方法的稳定性。可以有效地处理连续动作空间的问题。
🍈常见变体
Advantage Actor-Critic (A2C):使用优势函数(Advantage Function)来改进策略更新。Asynchronous Advantage Actor-Critic (A3C):通过异步更新多个线程或进程中的网络参数,提高训练效率。
🍈示例
🍍示例分析
考虑一个简单的小车在轨道上行驶的场景。状态可以是小车的位置和速度,动作是施加在小车上的力的大小和方向。Actor 网络根据当前的状态输出一个动作,Critic 网络评估这个动作在当前状态下的价值。
例如,如果小车靠近轨道终点且速度适中,Actor 选择一个适当的力来保持或加速前进,Critic 给出一个较高的价值评估。如果小车偏离轨道或速度过快,Critic 给出较低的价值评估,促使 Actor 调整策略。
🍍代码实现
<code>import tensorflow as tf
import numpy as np
# 定义 Actor 网络
class ActorNetwork(tf.keras.Model):
def __init__(self, num_states, num_actions, hidden_units):
super(ActorNetwork, self).__init__()
self.layer1 = tf.keras.layers.Dense(hidden_units, activation='relu')code>
self.layer2 = tf.keras.layers.Dense(hidden_units, activation='relu')code>
self.output_layer = tf.keras.layers.Dense(num_actions, activation='softmax')code>
def call(self, state):
x = self.layer1(state)
x = self.layer2(x)
return self.output_layer(x)
# 定义 Critic 网络
class CriticNetwork(tf.keras.Model):
def __init__(self, num_states, hidden_units):
super(CriticNetwork, self).__init__()
self.layer1 = tf.keras.layers.Dense(hidden_units, activation='relu')code>
self.layer2 = tf.keras.layers.Dense(hidden_units, activation='relu')code>
self.output_layer = tf.keras.layers.Dense(1)
def call(self, state):
x = self.layer1(state)
x = self.layer2(x)
return self.output_layer(x)
# 训练函数
def train_actor_critic(env, actor, critic, num_episodes, gamma):
optimizer_actor = tf.keras.optimizers.Adam(learning_rate=0.01)
optimizer_critic = tf.keras.optimizers.Adam(learning_rate=0.01)
for episode in range(num_episodes):
state = env.reset()
state = tf.convert_to_tensor(state, dtype=tf.float32)
done = False
rewards = []
states = []
actions = []
while not done:
# Actor 选择动作
action_probs = actor(state)
action = np.random.choice(np.arange(len(action_probs)), p=action_probs.numpy()[0])
# 与环境交互
next_state, reward, done, _ = env.step(action)
next_state = tf.convert_to_tensor(next_state, dtype=tf.float32)
# 存储信息
rewards.append(reward)
states.append(state)
actions.append(action)
state = next_state
# 计算折扣回报
discounted_rewards = []
cumulative_reward = 0
for reward in rewards[::-1]:
cumulative_reward = reward + gamma * cumulative_reward
discounted_rewards.append(cumulative_reward)
discounted_rewards = discounted_rewards[::-1]
# 训练 Critic
values = critic(tf.stack(states))
value_loss = tf.keras.losses.MeanSquaredError()(tf.convert_to_tensor(discounted_rewards), values)
optimizer_critic.minimize(value_loss, var_list=critic.trainable_variables)
# 计算优势值
advantages = tf.convert_to_tensor(discounted_rewards) - values
action_log_probs = tf.math.log(action_probs[0, actions])
# 训练 Actor
actor_loss = -tf.reduce_mean(action_log_probs * advantages)
optimizer_actor.minimize(actor_loss, var_list=actor.trainable_variables)
# 示例环境
class SimpleEnv:
def __init__(self):
self.state = np.random.rand(2) # 随机初始化状态
def reset(self):
self.state = np.random.rand(2)
return self.state
def step(self, action):
# 简单的环境反馈,仅用于示例
if action == 0:
self.state += np.array([0.1, 0])
elif action == 1:
self.state += np.array([0, 0.1])
reward = np.sum(self.state) # 简单的奖励计算
done = np.sum(self.state) > 1.5 # 结束条件
return self.state, reward, done, None
# 超参数
num_episodes = 1000
num_states = 2
num_actions = 2
hidden_units = 32
gamma = 0.99
# 创建网络和环境
actor = ActorNetwork(num_states, num_actions, hidden_units)
critic = CriticNetwork(num_states, hidden_units)
env = SimpleEnv()
# 训练
train_actor_critic(env, actor, critic, num_episodes, gamma)
🍉总结
强化学习是一种机器学习的重要分支,它专注于智能体如何在与环境的交互中通过试错来学习最优策略,以最大化累积奖励。
在强化学习中,智能体通过感知环境的状态,采取行动,并根据行动所获得的奖励来调整自己的策略。其核心概念包括状态、动作、奖励和策略。状态是对环境的描述,动作是智能体可执行的选择,奖励则是对智能体动作的反馈,策略决定了在给定状态下智能体采取何种动作。
强化学习的算法众多,如 Q-learning 算法,通过估计每个状态-动作对的价值来更新策略;SARSA 算法,在学习过程中同时考虑当前策略和下一时刻的策略;以及深度强化学习中的 DQN 算法,利用深度神经网络来近似价值函数。
强化学习在许多领域都有广泛应用。在机器人控制领域,它可以让机器人学会自主行走、抓取物体等复杂任务;在自动驾驶中,帮助车辆做出最优的驾驶决策;在游戏中,训练智能体达到超越人类玩家的水平。
然而,强化学习也面临一些挑战。例如,奖励的设计需要精心考量,否则可能导致智能体学习到不理想的策略;训练过程可能不稳定且耗时较长;在复杂环境中,模型的泛化能力也有待提高。
总的来说,强化学习为解决复杂的决策问题提供了有力的工具和方法,尽管存在挑战,但随着技术的不断发展,其应用前景十分广阔。


上一篇: 短短3个月“AI教母”李飞飞创造一家独角兽;OpenAI推出新算法帮助提升AI模型输出可读性 | AI头条...
下一篇: 【 香橙派 AIpro评测】烧系统运行部署LLMS大模型跑开源yolov5物体检测并体验Jupyter Lab AI 应用样例(新手入门)
本文标签
声明
本文内容仅代表作者观点,或转载于其他网站,本站不以此文作为商业用途
如有涉及侵权,请联系本站进行删除
转载本站原创文章,请注明来源及作者。

