背景

全波形反演技术 (Full waveform inversion, FWI[1]）是地震勘探领域的重要技术，也是目前该领域的前沿热点方向。该技术利用地震波模拟和数学优化方法，通过地表观测得到的地震数据来获取地下的地质特性分布，从而为后续的油气藏开发提供输入。由于其处理的波动问题是广泛存在的，因此该技术除了在地球物理之外，在医疗的超声成像领域[2]也有可观的应用前景。该问题是典型的涉及偏微分方程求解的反问题，当前业界常用的方法是利用有限差分、有限元法求解声波、弹性波方程，利用伴随方法进行反演，最终得到代表地下地质分布的速度模型。由于大规模的声波、弹性波方程数值求解需要巨大的HPC算力资源，因此工程中使用FWI技术十分昂贵。为了降低该技术的成本，目前学术界正在积极尝试利用AI方法辅助或替代现有的FWI技术。本文将首先介绍FWI方法的原理，然后简要概述当前AI方法在FWI当中的应用。

01

FWI原理

1.1 整体流程

地震勘探整体上包括数据采集、数据处理、数据解释等工作步骤。其中数据采集通过人工激发地震波，并利用分布在地表的检波器将地震波传播情况记录下来，得到地震数据。采集到的数据经过一系列处理 (静校正、去噪、反褶积、速度分析、动校正、水平叠加、偏移等) 后，就可作为FWI的输入，由FWI反演得到由速度模型表示的地震剖面。随后进行数据解释，即根据地震剖面确定地质构造形态和空间位置、推测地层的岩性、厚度及层间接触关系，确定地层含油气的可能性，为钻探提供准确的井位等。可见，在以上环节中，FWI的输入是地震波，输出是速度模型。

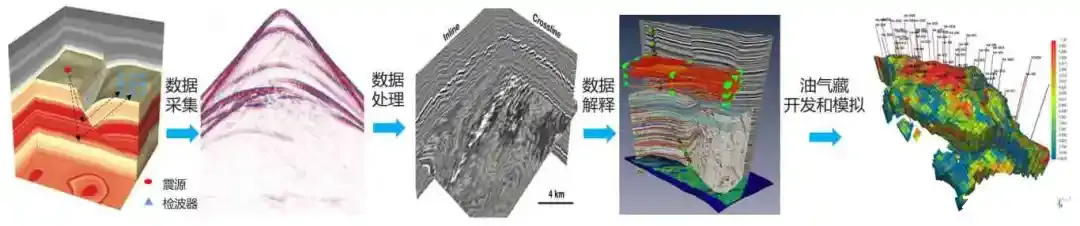
图1. 地震勘探的整体流程

1.2 正演过程

FWI的正演指的是针对假设的速度模型，通过数值求解声波或弹性波方程，得到地震波的时空分布。该问题的数学定义如表1所示。

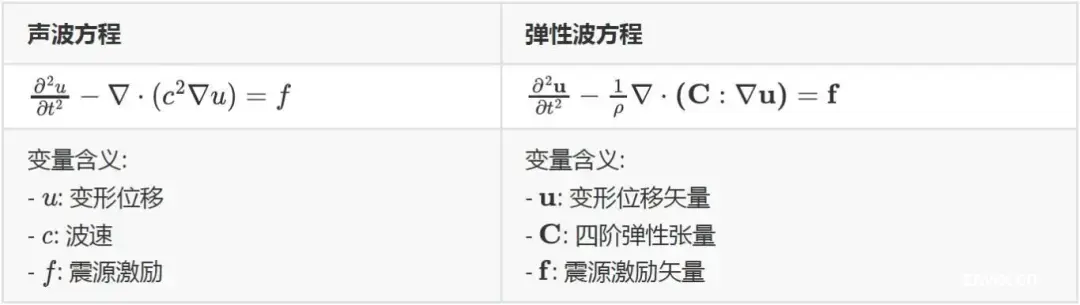
表1. 正演问题的数学方程定义

可以看出，声波方程的待求变量少，方程更简单，但是只有一个标量波速c来表征地质特性，不能反映地质的各向异性；弹性波方程中的弹性张量C是四阶对称张量，其最多可包含21个独立分量，因而可以表征各向异性的复杂地质特性，但相应地求解也更为复杂，计算和存储的需求更大。本文后续均以声波方程为例进行介绍。

波动方程求解方法可分为频域求解和时域求解，时域求解中时间积分可采用蛙跳格式或Runge-Kutta格式，针对空间导数又可采用有限差分、有限元、谱方法等。

1.3 反演过程

FWI是典型的反问题，需要从观测的地震数据推测地下速度模型的分布，而这一推测过程并没有数学方程可以描述，因此必须不断重复正演过程，迭代修正估计的速度模型，最终逼近真实的速度模型分布。整个反演算法的框架如图2所示。

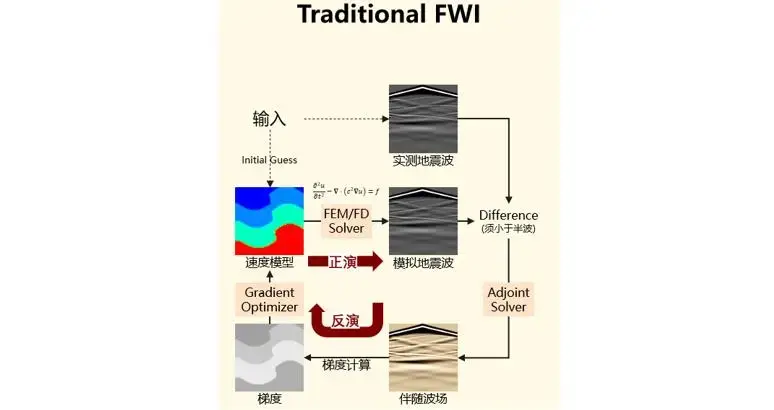
图2. FWI反演算法框架

传统的反演算法具体流程如下。首先，输入对速度模型的初始估计 (该初始估计已经90%接近于真实速度模型)，接着通过正演获得模拟地震波数据，将模拟地震波数据与观测的地震波数据进行比较，获得二者的差值。反演的目标是获得速度模型的修正量，能够使该差值降低，因此最直观的方法是求取插值对速度模型的梯度，利用梯度下降等优化方法进行优化。求梯度要求差值对速度模型的全导数，一般通过伴随方法来实现。

伴随方法是常用的求解PDE约束下的优化问题的方法，在当前问题中实施步骤如下。待优化的目标函数是模拟地震波u与实测地震波u_exp的差：

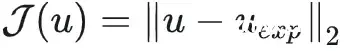
表2. 伴随方法的数学推导过程

由于梯度下降的每一次迭代中都需要完整模拟一次正演过程，因此该方法主要的计算量来源于多次的正演求解。此外，基于梯度的优化方法可能陷入局部最优解，因此对速度模型的初始估计需要较为准确，具体地，初始速度模型所对应的地震波场与实际地震波场的误差需小于半波长。

02

AI方法在 FWI 中的应用

2.1 InversionNet

用AI方法来辅助全波形反演最直观的方式就是用端到端的代理模型来直接学习地震数据到速度模型的直接映射。这类纯数据驱动方法的代表性工作是美国Los Alamos国家实验室的InversionNet[3]。InversionNet采用了Encoder-Decoder架构，其中Encoder学习地震数据的抽象特征并且将这些抽象特征映射为一个高维向量，而Decoder则将这个高维向量映射为速度模型。在Encoder和Decoder内部，采用CNN层作为网络的基础结构。整个模型结构如图3所示。除了InversionNet之外，该团队还继续开发了InversionNet3D[4]模型，将模型处理的反演任务从二维拓展到了三维。

​

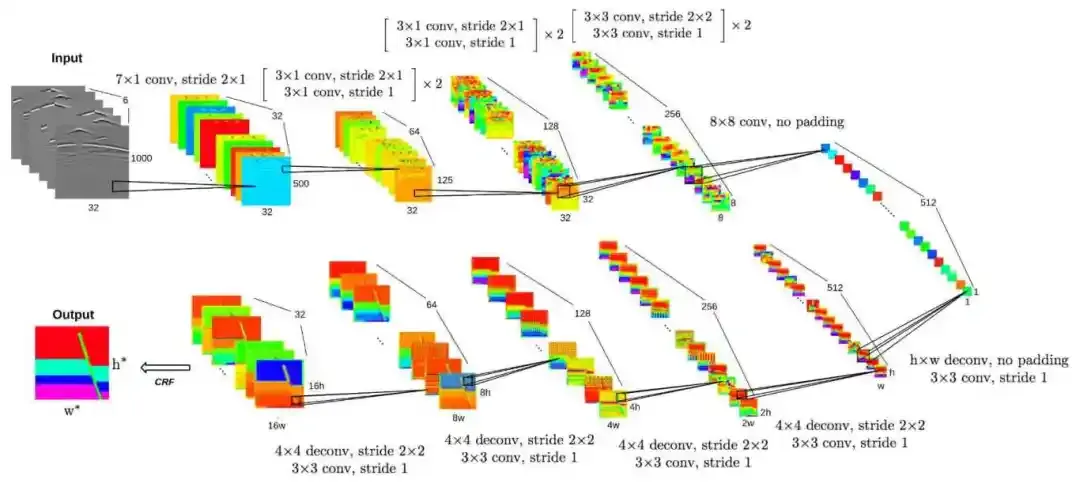
图3. InversionNet网络结构

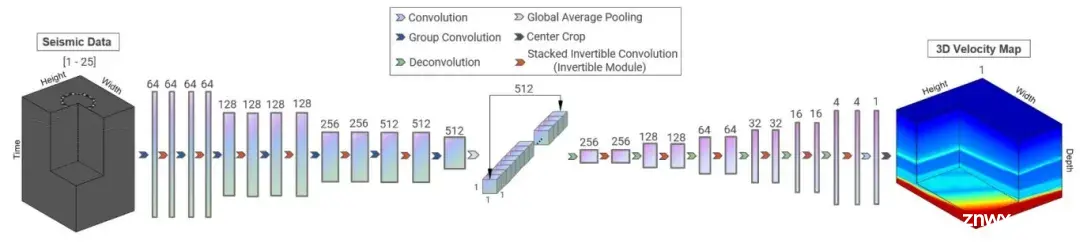
图4. InversionNet3D网络结构

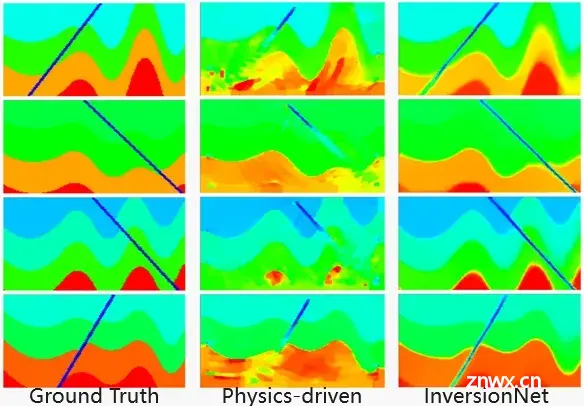
图5. InversionNet反演精度和传统方法对比

InversionNet的思路简单直观，其优势是反演精度高和速度快，劣势是训练数据需求量大和泛化性差。在有充足标签数据的情况下，InversionNet相较于传统物理驱动方法，反演的相对误差可以降低25-50%。并且训练好的InversionNet反演仅需一次网络推理，速度远快于传统物理驱动的方法，任务耗时约从小时级降为秒级。但在实际地震勘探场景中，难以获得充足的带标签数据来训练模型，因此限制了该方法在实际工业中的应用。

2.2 UPFWI

为避免训练数据缺失的问题，一条很自然的路径便是无监督训练。美国Los Alamos 国家实验联合宾州州立大学、密歇根州立大学和微软开发了UPFWI(Unsupervised Physics-informed Full-Waveform Inversion)[5]模型。该模型并不像InversionNet那样直接实现端到端映射，而是继承了传统正反演的基本框架，其核心特点是用可微分求解器处理正演过程，并用CNN来代理反演过程。将反演问题转化为数据重建问题，优化更新的对象不是速度模型，而是用于重建速度模型的CNN网络。同时，由于采用了可微分求解器，可以直接获取正演求解过程中所有变量的梯度，因而无需使用伴随方法。其实施流程如图6所示。

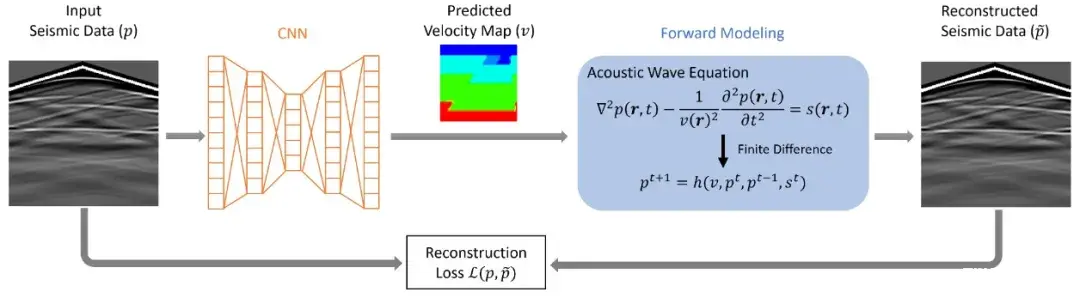
图6. UPFWI的结构示意图

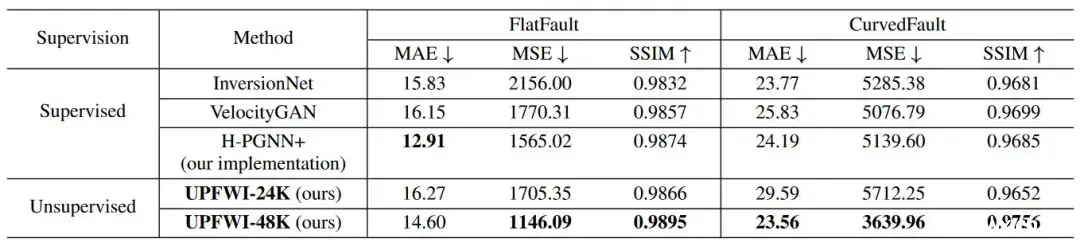
图7. UPFWI在数据集OpenFWI上的验证结果

2.3 PINN-FWI

PINNs6[6]作为一种通用的AI for PDE求解方法，也可用于FWI问题。PINNs方法的特点是将PDE作为物理约束加入loss中，学习从计算域坐标到物理场的映射。由于边界条件、初始条件、观测数据等其他约束也可以轻易地加入loss一并训练，因此该方法特别适合数据融合。

美国Brown大学开发了PINN-FWI[7]模型。该模型包含2个神经网络，网络1用于预测地震波场p，网络2用于预测速度场α，网络的输入为采样点的坐标(x,z,t)。训练的loss由两部分构成，一部分是网络输出的地震波场与观测值的差异，另一部分是物理约束，包括PDE的满足程度以及初始/边界条件的满足程度。PDE中的微分项可通过深度学习框架的自动微分来求得。模型训练时通过梯度下降算法优化两个神经网络中的可训练参数θ1和 θ2，当loss小于某一阈值时即可认为物理约束与观测数据匹配度同时得到满足。

该方法也是一种无监督训练方法，因此也不需要标签数据。除此之外，它的优点是不依赖网格，且方便融合多组不同形式的观测数据。而它的缺点是反演精度差，并且每次反演都对应一次网络训练过程，因此效率较低。

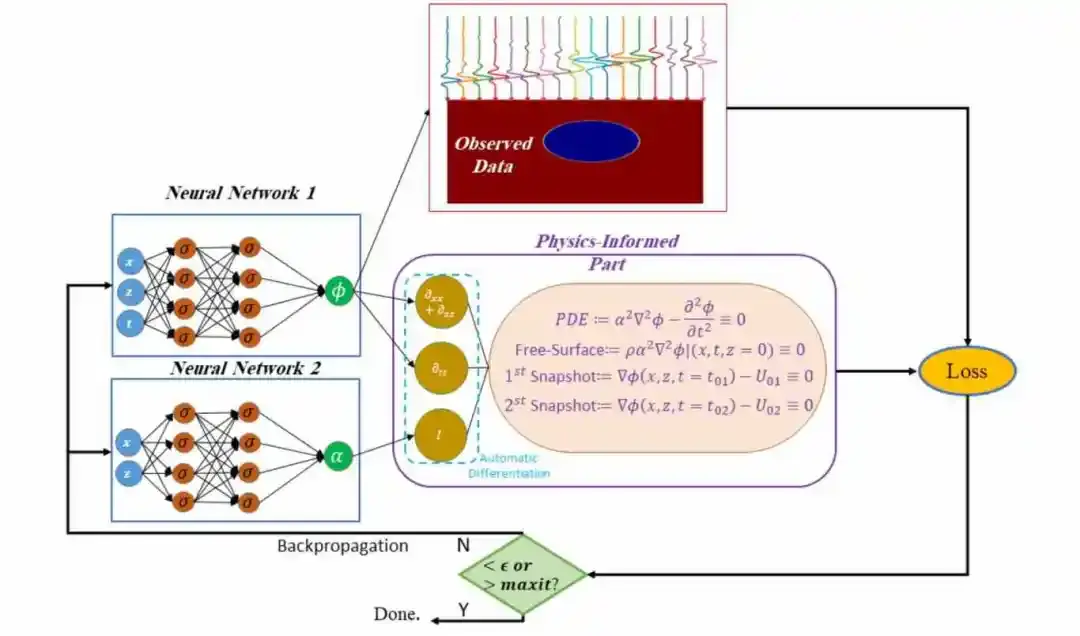
图8. PINN-FWI模型架构

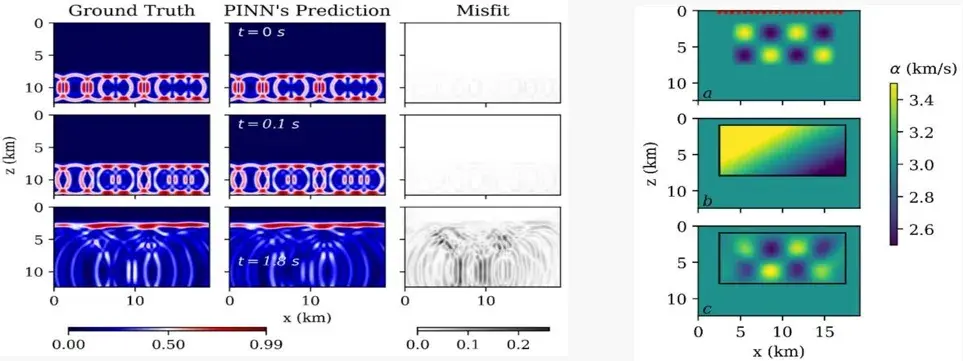
图9. PINN-FWI的反演效果：对波场p的预测精度较高，对速度α的反演精度较差

03

讨论

以上介绍了FWI的传统方法以及三种具有代表性的AI辅助FWI方法。这几种方法各有优劣，总结如下。

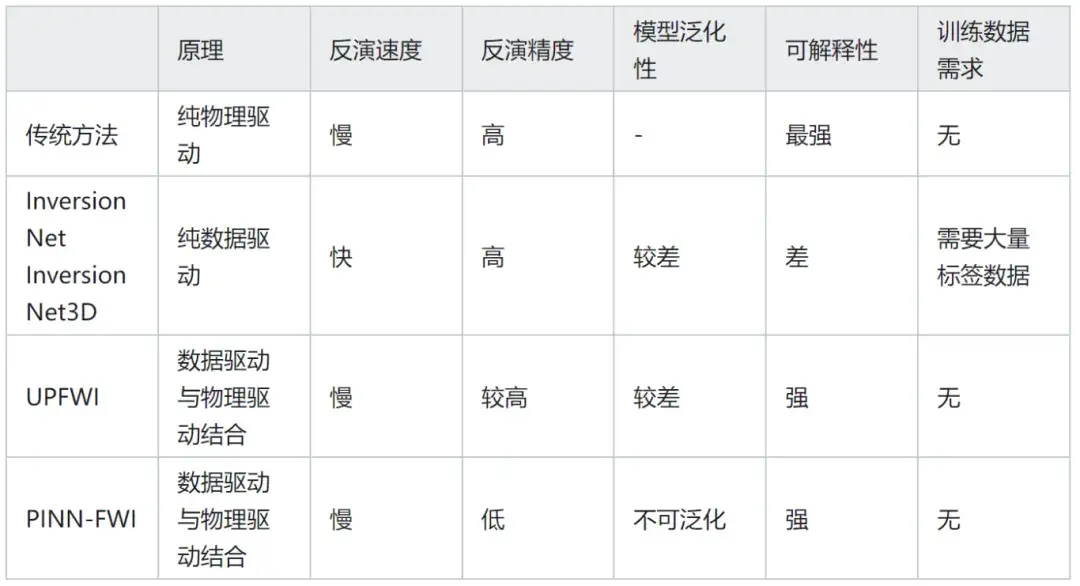
表3. FWI 各方法特点和优劣比较

笔者认为，纯数据驱动的方法需要大量标签数据，难以覆盖丰富的真实场景，因此距离工业应用尚存在一定距离，仅可在简单情况下作为辅助工具。而数据驱动与物理驱动结合的方法，更易与当前工业应用流程相结合，有望实际提升工业生产效率。但如何克服反演速度慢、模型泛化性差的问题，仍需进一步研究探索。

参考文献

[1] Fichtner, A., 2011. Full Seismic Waveform Modelling and Inversion, Advances in Geophysical and Environmental Mechanics and Mathematics. Springer Berlin Heidelberg, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-15807-0

[2] Guasch, L., Calderón Agudo, O., Tang, M.-X., Nachev, P., Warner, M., 2020. Full-waveform inversion imaging of the human

brain. npj Digit. Med. 3, 28. https://doi.org/10.1038/s41746-020-0240-8

[3] Wu, Y., Lin, Y., 2020. InversionNet: A Real-Time and Accurate Full Waveform Inversion with CNNs and continuous CRFs.

IEEE Trans. Comput. Imaging 6, 419–433. https://doi.org/10.1109/TCI.2019.2956866

[4] Zeng, Q., Feng, S., Wohlberg, B., Lin, Y., 2022. InversionNet3D: Efficient and Scalable Learning for 3-D Full-Waveform

Inversion. IEEE Trans. Geosci. Remote Sensing 60, 1–16. https://doi.org/10.1109/TGRS.2021.3135354

[5] Jin, P., Zhang, X., Chen, Y., Huang, S.X., Liu, Z., Lin, Y., 2022. Unsupervised Learning of Full-Waveform Inversion:

Connecting CNN and Partial Differential Equation in a Loop. http://arxiv.org/abs/2110.07584]

[6] Raissi, M., Perdikaris, P., Karniadakis, G.E., 2019. Physics-informed neural networks: A deep learning framework for solving

forward and inverse problems involving nonlinear partial differential equations. Journal of Computational Physics 378, 686–707.

https://doi.org/10.1016/j.jcp.2018.10.045

[7] Rasht‐Behesht, M., Huber, C., Shukla, K., Karniadakis, G.E., 2022. Physics‐Informed Neural Networks (PINNs) for Wave

Propagation and Full Waveform Inversions. Journal of Geophysical Research: Solid Earth 127. https://

doi.org/10.1029/2021jb023120